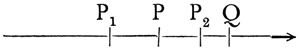LECTURE VI. THE PROBLEM OF INFINITY CONSIDERED HISTORICALLYIt will be remembered that, when we enumerated the grounds upon which the reality of the sensible world has been questioned, one of those mentioned was the supposed impossibility of infinity and continuity. In view of our earlier discussion of physics, it would seem that no conclusive empirical evidence exists in favour of infinity or continuity in objects of sense or in matter. Nevertheless, the explanation which assumes infinity and continuity remains incomparably easier and more natural, from a scientific point of view, than any other, and since Georg Cantor has shown that the supposed contradictions are illusory, there is no longer any reason to struggle after a finitist explanation of the world.
The supposed difficulties of continuity all have their source in the fact that a continuous series must have an infinite number of terms, and are in fact difficulties concerning infinity. Hence, in freeing the infinite from contradiction, we are at the same time showing the logical possibility of continuity as assumed in science.
The kind of way in which infinity has been used to discredit the world of sense may be illustrated by Kant's first two antinomies. In the first, the thesis states: “The world has a beginning in time, and as regards space is enclosed within limits”; the antithesis states: “The world has no beginning and no limits in space, but is infinite in respect of both time and space.” Kant professes to prove both these propositions, whereas, if what we have said on modern logic has any truth, it must be impossible to prove either. In order, however, to rescue the world of sense, it is enough to destroy the proof of one of the two. For our present purpose, it is the proof that the world is finite that interests us. Kant's argument as regards space here rests upon his argument as regards time. We need therefore only examine the argument as regards time. What he says is as follows:
“For let us assume that the world has no beginning as regards time, so that up to every given instant an eternity has elapsed, and therefore an infinite series of successive states of the things in the world has passed by. But the infinity of a series consists just in this, that it can never be completed by successive synthesis. Therefore an infinite past world-series is impossible, and accordingly a beginning of the world is a necessary condition of its existence; which was the first thing to be proved.”
Many different criticisms might be passed on this argument, but we will content ourselves with a bare minimum. To begin with, it is a mistake to define the infinity of a series as “impossibility of completion by successive synthesis.” The notion of infinity, as we shall see in the next lecture, is primarily a property of classes, and only derivatively applicable to series; classes which are infinite are given all at once by the defining property of their members, so that there is no question of “completion” or of “successive synthesis.” And the word “synthesis,” by suggesting the mental activity of synthesising, introduces, more or less surreptitiously, that reference to mind by which all Kant's philosophy was infected. In the second place, when Kant says that an infinite series can “never” be completed by successive synthesis, all that he has even conceivably a right to say is that it cannot be completed in a finite time. Thus what he really proves is, at most, that if the world had no beginning, it must have already existed for an infinite time. This, however, is a very poor conclusion, by no means suitable for his purposes. And with this result we might, if we chose, take leave of the first antinomy.
It is worth while, however, to consider how Kant came to make such an elementary blunder. What happened in his imagination was obviously something like this: Starting from the present and going backwards in time, we have, if the world had no beginning, an infinite series of events. As we see from the word “synthesis,” he imagined a mind trying to grasp these successively, in the reverse order to that in which they had occurred, i.e. going from the present backwards. This series is obviously one which has no end. But the series of events up to the present has an end, since it ends with the present. Owing to the inveterate subjectivism of his mental habits, he failed to notice that he had reversed the sense of the series by substituting backward synthesis for forward happening, and thus he supposed that it was necessary to identify the mental series, which had no end, with the physical series, which had an end but no beginning. It was this mistake, I think, which, operating unconsciously, led him to attribute validity to a singularly flimsy piece of fallacious reasoning.
The second antinomy illustrates the dependence of the problem of continuity upon that of infinity. The thesis states: “Every complex substance in the world consists of simple parts, and there exists everywhere nothing but the simple or what is composed of it.” The antithesis states: “No complex thing in the world consists of simple parts, and everywhere in it there exists nothing simple.” Here, as before, the proofs of both thesis and antithesis are open to criticism, but for the purpose of vindicating physics and the world of sense it is enough to find a fallacy in one of the proofs. We will choose for this purpose the proof of the antithesis, which begins as follows:
“Assume that a complex thing (as substance) consists of simple parts. Since all external relation, and therefore all composition out of substances, is only possible in space, the space occupied by a complex thing must consist of as many parts as the thing consists of. Now space does not consist of simple parts, but of spaces.”
The rest of his argument need not concern us, for the nerve of the proof lies in the one statement: “Space does not consist of simple parts, but of spaces.” This is like Bergson's objection to “the absurd proposition that motion is made up of immobilities.” Kant does not tell us why he holds that a space must consist of spaces rather than of simple parts. Geometry regards space as made up of points, which are simple; and although, as we have seen, this view is not scientifically or logically necessary, it remains primâ facie possible, and its mere possibility is enough to vitiate Kant's argument. For, if his proof of the thesis of the antinomy were valid, and if the antithesis could only be avoided by assuming points, then the antinomy itself would afford a conclusive reason in favour of points. Why, then, did Kant think it impossible that space should be composed of points?
I think two considerations probably influenced him. In the first place, the essential thing about space is spatial order, and mere points, by themselves, will not account for spatial order. It is obvious that his argument assumes absolute space; but it is spatial relations that are alone important, and they cannot be reduced to points. This ground for his view depends, therefore, upon his ignorance of the logical theory of order and his oscillations between absolute and relative space. But there is also another ground for his opinion, which is more relevant to our present topic. This is the ground derived from infinite divisibility. A space may be halved, and then halved again, and so on ad infinitum, and at every stage of the process the parts are still spaces, not points. In order to reach points by such a method, it would be necessary to come to the end of an unending process, which is impossible. But just as an infinite class can be given all at once by its defining concept, though it cannot be reached by successive enumeration, so an infinite set of points can be given all at once as making up a line or area or volume, though they can never be reached by the process of successive division. Thus the infinite divisibility of space gives no ground for denying that space is composed of points. Kant does not give his grounds for this denial, and we can therefore only conjecture what they were. But the above two grounds, which we have seen to be fallacious, seem sufficient to account for his opinion, and we may therefore conclude that the antithesis of the second antinomy is unproved.
The above illustration of Kant's antinomies has only been introduced in order to show the relevance of the problem of infinity to the problem of the reality of objects of sense. In the remainder of the present lecture, I wish to state and explain the problem of infinity, to show how it arose, and to show the irrelevance of all the solutions proposed by philosophers. In the following lecture, I shall try to explain the true solution, which has been discovered by the mathematicians, but nevertheless belongs essentially to philosophy. The solution is definitive, in the sense that it entirely satisfies and convinces all who study it carefully. For over two thousand years the human intellect was baffled by the problem; its many failures and its ultimate success make this problem peculiarly apt for the illustration of method.
The problem appears to have first arisen in some such way as the following.[22] Pythagoras and his followers, who were interested, like Descartes, in the application of number to geometry, adopted in that science more arithmetical methods than those with which Euclid has made us familiar. They, or their contemporaries the atomists, believed, apparently, that space is composed of indivisible points, while time is composed of indivisible instants.[23] This belief would not, by itself, have raised the difficulties which they encountered, but it was presumably accompanied by another belief, that the number of points in any finite area or of instants in any finite period must be finite. I do not suppose that this latter belief was a conscious one, because probably no other possibility had occurred to them. But the belief nevertheless operated, and very soon brought them into conflict with facts which they themselves discovered. Before explaining how this occurred, however, it is necessary to say one word in explanation of the phrase “finite number.” The exact explanation is a matter for our next lecture; for the present, it must suffice to say that I mean 0 and 1 and 2 and 3 and so on, for ever—in other words, any number that can be obtained by successively adding ones. This includes all the numbers that can be expressed by means of our ordinary numerals, and since such numbers can be made greater and greater, without ever reaching an unsurpassable maximum, it is easy to suppose that there are no other numbers. But this supposition, natural as it is, is mistaken.
Whether the Pythagoreans themselves believed space and time to be composed of indivisible points and instants is a debatable question.[24] It would seem that the distinction between space and matter had not yet been clearly made, and that therefore, when an atomistic view is expressed, it is difficult to decide whether particles of matter or points of space are intended. There is an interesting passage[25] in Aristotle's Physics,[26] where he says:
“The Pythagoreans all maintained the existence of the void, and said that it enters into the heaven itself from the boundless breath, inasmuch as the heaven breathes in the void also; and the void differentiates natures, as if it were a sort of separation of consecutives, and as if it were their differentiation; and that this also is what is first in numbers, for it is the void which differentiates them.”
This seems to imply that they regarded matter as consisting of atoms with empty space in between. But if so, they must have thought space could be studied by only paying attention to the atoms, for otherwise it would be hard to account for their arithmetical methods in geometry, or for their statement that “things are numbers.”
The difficulty which beset the Pythagoreans in their attempts to apply numbers arose through their discovery of incommensurables, and this, in turn, arose as follows. Pythagoras, as we all learnt in youth, discovered the proposition that the sum of the squares on the sides of a right-angled triangle is equal to the square on the hypotenuse. It is said that he sacrificed an ox when he discovered this theorem; if so, the ox was the first martyr to science. But the theorem, though it has remained his chief claim to immortality, was soon found to have a consequence fatal to his whole philosophy. Consider the case of a right-angled triangle whose two sides are equal, such a triangle as is formed by two sides of a square and a diagonal. Here, in virtue of the theorem, the square on the diagonal is double of the square on either of the sides. But Pythagoras or his early followers easily proved that the square of one whole number cannot be double of the square of another.[27] Thus the length of the side and the length of the diagonal are incommensurable; that is to say, however small a unit of length you take, if it is contained an exact number of times in the side, it is not contained any exact number of times in the diagonal, and vice versa.
Now this fact might have been assimilated by some philosophies without any great difficulty, but to the philosophy of Pythagoras it was absolutely fatal. Pythagoras held that number is the constitutive essence of all things, yet no two numbers could express the ratio of the side of a square to the diagonal. It would seem probable that we may expand his difficulty, without departing from his thought, by assuming that he regarded the length of a line as determined by the number of atoms contained in it—a line two inches long would contain twice as many atoms as a line one inch long, and so on. But if this were the truth, then there must be a definite numerical ratio between any two finite lengths, because it was supposed that the number of atoms in each, however large, must be finite. Here there was an insoluble contradiction. The Pythagoreans, it is said, resolved to keep the existence of incommensurables a profound secret, revealed only to a few of the supreme heads of the sect; and one of their number, Hippasos of Metapontion, is even said to have been shipwrecked at sea for impiously disclosing the terrible discovery to their enemies. It must be remembered that Pythagoras was the founder of a new religion as well as the teacher of a new science: if the science came to be doubted, the disciples might fall into sin, and perhaps even eat beans, which according to Pythagoras is as bad as eating parents' bones.
The problem first raised by the discovery of incommensurables proved, as time went on, to be one of the most severe and at the same time most far-reaching problems that have confronted the human intellect in its endeavour to understand the world. It showed at once that numerical measurement of lengths, if it was to be made accurate, must require an arithmetic more advanced and more difficult than any that the ancients possessed. They therefore set to work to reconstruct geometry on a basis which did not assume the universal possibility of numerical measurement—a reconstruction which, as may be seen in Euclid, they effected with extraordinary skill and with great logical acumen. The moderns, under the influence of Cartesian geometry, have reasserted the universal possibility of numerical measurement, extending arithmetic, partly for that purpose, so as to include what are called “irrational” numbers, which give the ratios of incommensurable lengths. But although irrational numbers have long been used without a qualm, it is only in quite recent years that logically satisfactory definitions of them have been given. With these definitions, the first and most obvious form of the difficulty which confronted the Pythagoreans has been solved; but other forms of the difficulty remain to be considered, and it is these that introduce us to the problem of infinity in its pure form.
We saw that, accepting the view that a length is composed of points, the existence of incommensurables proves that every finite length must contain an infinite number of points. In other words, if we were to take away points one by one, we should never have taken away all the points, however long we continued the process. The number of points, therefore, cannot be counted, for counting is a process which enumerates things one by one. The property of being unable to be counted is characteristic of infinite collections, and is a source of many of their paradoxical qualities. So paradoxical are these qualities that until our own day they were thought to constitute logical contradictions. A long line of philosophers, from Zeno[28] to M. Bergson, have based much of their metaphysics upon the supposed impossibility of infinite collections. Broadly speaking, the difficulties were stated by Zeno, and nothing material was added until we reach Bolzano's Paradoxien des Unendlichen, a little work written in 1847–8, and published posthumously in 1851. Intervening attempts to deal with the problem are futile and negligible. The definitive solution of the difficulties is due, not to Bolzano, but to Georg Cantor, whose work on this subject first appeared in 1882.
In order to understand Zeno, and to realise how little modern orthodox metaphysics has added to the achievements of the Greeks, we must consider for a moment his master Parmenides, in whose interest the paradoxes were invented.[29] Parmenides expounded his views in a poem divided into two parts, called “the way of truth” and “the way of opinion”—like Mr Bradley's “Appearance” and “Reality,” except that Parmenides tells us first about reality and then about appearance. “The way of opinion,” in his philosophy, is, broadly speaking, Pythagoreanism; it begins with a warning: “Here I shall close my trustworthy speech and thought about the truth. Henceforward learn the opinions of mortals, giving ear to the deceptive ordering of my words.” What has gone before has been revealed by a goddess, who tells him what really is. Reality, she says, is uncreated, indestructible, unchanging, indivisible; it is “immovable in the bonds of mighty chains, without beginning and without end; since coming into being and passing away have been driven afar, and true belief has cast them away.” The fundamental principle of his inquiry is stated in a sentence which would not be out of place in Hegel:[30] “Thou canst not know what is not—that is impossible—nor utter it; for it is the same thing that can be thought and that can be.” And again: “It needs must be that what can be thought and spoken of is; for it is possible for it to be, and it is not possible for what is nothing to be.” The impossibility of change follows from this principle; for what is past can be spoken of, and therefore, by the principle, still is.
The great conception of a reality behind the passing illusions of sense, a reality one, indivisible, and unchanging, was thus introduced into Western philosophy by Parmenides, not, it would seem, for mystical or religious reasons, but on the basis of a logical argument as to the impossibility of not-being. All the great metaphysical systems—notably those of Plato, Spinoza, and Hegel—are the outcome of this fundamental idea. It is difficult to disentangle the truth and the error in this view. The contention that time is unreal and that the world of sense is illusory must, I think, be regarded as based upon fallacious reasoning. Nevertheless, there is some sense—easier to feel than to state—in which time is an unimportant and superficial characteristic of reality. Past and future must be acknowledged to be as real as the present, and a certain emancipation from slavery to time is essential to philosophic thought. The importance of time is rather practical than theoretical, rather in relation to our desires than in relation to truth. A truer image of the world, I think, is obtained by picturing things as entering into the stream of time from an eternal world outside, than from a view which regards time as the devouring tyrant of all that is. Both in thought and in feeling, to realise the unimportance of time is the gate of wisdom. But unimportance is not unreality; and therefore what we shall have to say about Zeno's arguments in support of Parmenides must be mainly critical.
The relation of Zeno to Parmenides is explained by Plato[31] in the dialogue in which Socrates, as a young man, learns logical acumen and philosophic disinterestedness from their dialectic. I quote from Jowett's translation:
“I see, Parmenides, said Socrates, that Zeno is your second self in his writings too; he puts what you say in another way, and would fain deceive us into believing that he is telling us what is new. For you, in your poems, say All is one, and of this you adduce excellent proofs; and he on the other hand says There is no Many; and on behalf of this he offers overwhelming evidence. To deceive the world, as you have done, by saying the same thing in different ways, one of you affirming the one, and the other denying the many, is a strain of art beyond the reach of most of us.
“Yes, Socrates, said Zeno. But although you are as keen as a Spartan hound in pursuing the track, you do not quite apprehend the true motive of the composition, which is not really such an ambitious work as you imagine; for what you speak of was an accident; I had no serious intention of deceiving the world. The truth is, that these writings of mine were meant to protect the arguments of Parmenides against those who scoff at him and show the many ridiculous and contradictory results which they suppose to follow from the affirmation of the one. My answer is an address to the partisans of the many, whose attack I return with interest by retorting upon them that their hypothesis of the being of the many if carried out appears in a still more ridiculous light than the hypothesis of the being of the one.”
Zeno's four arguments against motion were intended to exhibit the contradictions that result from supposing that there is such a thing as change, and thus to support the Parmenidean doctrine that reality is unchanging.[32] Unfortunately, we only know his arguments through Aristotle,[33] who stated them in order to refute them. Those philosophers in the present day who have had their doctrines stated by opponents will realise that a just or adequate presentation of Zeno's position is hardly to be expected from Aristotle; but by some care in interpretation it seems possible to reconstruct the so-called “sophisms” which have been “refuted” by every tyro from that day to this.
Zeno's arguments would seem to be “ad hominem”; that is to say, they seem to assume premisses granted by his opponents, and to show that, granting these premisses, it is possible to deduce consequences which his opponents must deny. In order to decide whether they are valid arguments or “sophisms,” it is necessary to guess at the tacit premisses, and to decide who was the “homo” at whom they were aimed. Some maintain that they were aimed at the Pythagoreans,[34] while others have held that they were intended to refute the atomists.[35] M. Evellin, on the contrary, holds that they constitute a refutation of infinite divisibility,[36] while M. G. Noël, in the interests of Hegel, maintains that the first two arguments refute infinite divisibility, while the next two refute indivisibles.[37] Amid such a bewildering variety of interpretations, we can at least not complain of any restrictions on our liberty of choice.
The historical questions raised by the above-mentioned discussions are no doubt largely insoluble, owing to the very scanty material from which our evidence is derived. The points which seem fairly clear are the following: (1) That, in spite of MM. Milhaud and Paul Tannery, Zeno is anxious to prove that motion is really impossible, and that he desires to prove this because he follows Parmenides in denying plurality;[38] (2) that the third and fourth arguments proceed on the hypothesis of indivisibles, a hypothesis which, whether adopted by the Pythagoreans or not, was certainly much advocated, as may be seen from the treatise On Indivisible Lines attributed to Aristotle. As regards the first two arguments, they would seem to be valid on the hypothesis of indivisibles, and also, without this hypothesis, to be such as would be valid if the traditional contradictions in infinite numbers were insoluble, which they are not.
We may conclude, therefore, that Zeno's polemic is directed against the view that space and time consist of points and instants; and that as against the view that a finite stretch of space or time consists of a finite number of points and instants, his arguments are not sophisms, but perfectly valid.
The conclusion which Zeno wishes us to draw is that plurality is a delusion, and spaces and times are really indivisible. The other conclusion which is possible, namely, that the number of points and instants is infinite, was not tenable so long as the infinite was infected with contradictions. In a fragment which is not one of the four famous arguments against motion, Zeno says:
“If things are a many, they must be just as many as they are, and neither more nor less. Now, if they are as many as they are, they will be finite in number.
“If things are a many, they will be infinite in number; for there will always be other things between them, and others again between these. And so things are infinite in number.”[39]
This argument attempts to prove that, if there are many things, the number of them must be both finite and infinite, which is impossible; hence we are to conclude that there is only one thing. But the weak point in the argument is the phrase: “If they are just as many as they are, they will be finite in number.” This phrase is not very clear, but it is plain that it assumes the impossibility of definite infinite numbers. Without this assumption, which is now known to be false, the arguments of Zeno, though they suffice (on certain very reasonable assumptions) to dispel the hypothesis of finite indivisibles, do not suffice to prove that motion and change and plurality are impossible. They are not, however, on any view, mere foolish quibbles: they are serious arguments, raising difficulties which it has taken two thousand years to answer, and which even now are fatal to the teachings of most philosophers.
The first of Zeno's arguments is the argument of the race-course, which is paraphrased by Burnet as follows:[40]
“You cannot get to the end of a race-course. You cannot traverse an infinite number of points in a finite time. You must traverse the half of any given distance before you traverse the whole, and the half of that again before you can traverse it. This goes on ad infinitum, so that there are an infinite number of points in any given space, and you cannot touch an infinite number one by one in a finite time.”[41]
Zeno appeals here, in the first place, to the fact that any distance, however small, can be halved. From this it follows, of course, that there must be an infinite number of points in a line. But, Aristotle represents him as arguing, you cannot touch an infinite number of points one by one in a finite time. The words “one by one” are important. (1) If all the points touched are concerned, then, though you pass through them continuously, you do not touch them “one by one.” That is to say, after touching one, there is not another which you touch next: no two points are next each other, but between any two there are always an infinite number of others, which cannot be enumerated one by one. (2) If, on the other hand, only the successive middle points are concerned, obtained by always halving what remains of the course, then the points are reached one by one, and, though they are infinite in number, they are in fact all reached in a finite time. His argument to the contrary may be supposed to appeal to the view that a finite time must consist of a finite number of instants, in which case what he says would be perfectly true on the assumption that the possibility of continued dichotomy is undeniable. If, on the other hand, we suppose the argument directed against the partisans of infinite divisibility, we must suppose it to proceed as follows:[42] “The points given by successive halving of the distances still to be traversed are infinite in number, and are reached in succession, each being reached a finite time later than its predecessor; but the sum of an infinite number of finite times must be infinite, and therefore the process will never be completed.” It is very possible that this is historically the right interpretation, but in this form the argument is invalid. If half the course takes half a minute, and the next quarter takes a quarter of a minute, and so on, the whole course will take a minute. The apparent force of the argument, on this interpretation, lies solely in the mistaken supposition that there cannot be anything beyond the whole of an infinite series, which can be seen to be false by observing that 1 is beyond the whole of the infinite series 1⁄2, 3⁄4, 7⁄8, 15⁄16, …
The second of Zeno's arguments is the one concerning Achilles and the tortoise, which has achieved more notoriety than the others. It is paraphrased by Burnet as follows:[43]
“Achilles will never overtake the tortoise. He must first reach the place from which the tortoise started. By that time the tortoise will have got some way ahead. Achilles must then make up that, and again the tortoise will be ahead. He is always coming nearer, but he never makes up to it.”[44]
This argument is essentially the same as the previous one. It shows that, if Achilles ever overtakes the tortoise, it must be after an infinite number of instants have elapsed since he started. This is in fact true; but the view that an infinite number of instants make up an infinitely long time is not true, and therefore the conclusion that Achilles will never overtake the tortoise does not follow.
The third argument,[45] that of the arrow, is very interesting. The text has been questioned. Burnet accepts the alterations of Zeller, and paraphrases thus:
“The arrow in flight is at rest. For, if everything is at rest when it occupies a space equal to itself, and what is in flight at any given moment always occupies a space equal to itself, it cannot move.”
But according to Prantl, the literal translation of the unemended text of Aristotle's statement of the argument is as follows: “If everything, when it is behaving in a uniform manner, is continually either moving or at rest, but what is moving is always in the now, then the moving arrow is motionless.” This form of the argument brings out its force more clearly than Burnet's paraphrase.
Here, if not in the first two arguments, the view that a finite part of time consists of a finite series of successive instants seems to be assumed; at any rate the plausibility of the argument seems to depend upon supposing that there are consecutive instants. Throughout an instant, it is said, a moving body is where it is: it cannot move during the instant, for that would require that the instant should have parts. Thus, suppose we consider a period consisting of a thousand instants, and suppose the arrow is in flight throughout this period. At each of the thousand instants, the arrow is where it is, though at the next instant it is somewhere else. It is never moving, but in some miraculous way the change of position has to occur between the instants, that is to say, not at any time whatever. This is what M. Bergson calls the cinematographic representation of reality. The more the difficulty is meditated, the more real it becomes. The solution lies in the theory of continuous series: we find it hard to avoid supposing that, when the arrow is in flight, there is a next position occupied at the next moment; but in fact there is no next position and no next moment, and when once this is imaginatively realised, the difficulty is seen to disappear.
The fourth and last of Zeno's arguments is[46] the argument of the stadium.
The argument as stated by Burnet is as follows:
First Position. / Second Position.
A . . . . / A . . . .
B . . . . / B . . . .
C . . . . / C . . . .
“Half the time may be equal to double the time. Let us suppose three rows of bodies, one of which (A) is at rest while the other two (B, C) are moving with equal velocity in opposite directions. By the time they are all in the same part of the course, B will have passed twice as many of the bodies in C as in A. Therefore the time which it takes to pass C is twice as long as the time it takes to pass A. But the time which B and C take to reach the position of A is the same. Therefore double the time is equal to the half.”
Gaye[47] devoted an interesting article to the interpretation of this argument. His translation of Aristotle's statement is as follows:
“The fourth argument is that concerning the two rows of bodies, each row being composed of an equal number of bodies of equal size, passing each other on a race-course as they proceed with equal velocity in opposite directions, the one row originally occupying the space between the goal and the middle point of the course, and the other that between the middle point and the starting-post. This, he thinks, involves the conclusion that half a given time is equal to double the time. The fallacy of the reasoning lies in the assumption that a body occupies an equal time in passing with equal velocity a body that is in motion and a body of equal size that is at rest, an assumption which is false. For instance (so runs the argument), let A A … be the stationary bodies of equal size, B B … the bodies, equal in number and in size to A A …, originally occupying the half of the course from the starting-post to the middle of the A's, and C C … those originally occupying the other half from the goal to the middle of the A's, equal in number, size, and velocity, to B B … Then three consequences follow. First, as the B's and C's pass one another, the first B reaches the last C at the same moment at which the first C reaches the last B. Secondly, at this moment the first C has passed all the A's, whereas the first B has passed only half the A's and has consequently occupied only half the time occupied by the first C, since each of the two occupies an equal time in passing each A. Thirdly, at the same moment all the B's have passed all the C's: for the first C and the first B will simultaneously reach the opposite ends of the course, since (so says Zeno) the time occupied by the first C in passing each of the B's is equal to that occupied by it in passing each of the A's, because an equal time is occupied by both the first B and the first C in passing all the A's. This is the argument: but it presupposes the aforesaid fallacious assumption.”

This argument is not quite easy to follow, and it is only valid as against the assumption that a finite time consists of a finite number of instants. We may re-state it in different language. Let us suppose three drill-sergeants, A, A′, and A″, standing in a row, while the two files of soldiers march past them in opposite directions. At the first moment which we consider, the three men B, B′, B″ in one row, and the three men C, C′, C″ in the other row, are respectively opposite to A, A′, and A″. At the very next moment, each row has moved on, and now B and C″ are opposite A′. Thus B and C″ are opposite each other. When, then, did B pass C′? It must have been somewhere between the two moments which we supposed consecutive, and therefore the two moments cannot really have been consecutive. It follows that there must be other moments between any two given moments, and therefore that there must be an infinite number of moments in any given interval of time.
The above difficulty, that B must have passed C′ at some time between two consecutive moments, is a genuine one, but is not precisely the difficulty raised by Zeno. What Zeno professes to prove is that “half of a given time is equal to double that time.” The most intelligible explanation of the argument known to me is that of Gaye.[48] Since, however, his explanation is not easy to set forth shortly, I will re-state what seems to me to be the logical essence of Zeno's contention. If we suppose that time consists of a series of consecutive instants, and that motion consists in passing through a series of consecutive points, then the fastest possible motion is one which, at each instant, is at a point consecutive to that at which it was at the previous instant. Any slower motion must be one which has intervals of rest interspersed, and any faster motion must wholly omit some points. All this is evident from the fact that we cannot have more than one event for each instant. But now, in the case of our A's and B's and C's, B is opposite a fresh A every instant, and therefore the number of A's passed gives the number of instants since the beginning of the motion. But during the motion B has passed twice as many C's, and yet cannot have passed more than one each instant. Hence the number of instants since the motion began is twice the number of A's passed, though we previously found it was equal to this number. From this result, Zeno's conclusion follows.
Zeno's arguments, in some form, have afforded grounds for almost all the theories of space and time and infinity which have been constructed from his day to our own. We have seen that all his arguments are valid (with certain reasonable hypotheses) on the assumption that finite spaces and times consist of a finite number of points and instants, and that the third and fourth almost certainly in fact proceeded on this assumption, while the first and second, which were perhaps intended to refute the opposite assumption, were in that case fallacious. We may therefore escape from his paradoxes either by maintaining that, though space and time do consist of points and instants, the number of them in any finite interval is infinite; or by denying that space and time consist of points and instants at all; or lastly, by denying the reality of space and time altogether. It would seem that Zeno himself, as a supporter of Parmenides, drew the last of these three possible deductions, at any rate in regard to time. In this a very large number of philosophers have followed him. Many others, like M. Bergson, have preferred to deny that space and time consist of points and instants. Either of these solutions will meet the difficulties in the form in which Zeno raised them. But, as we saw, the difficulties can also be met if infinite numbers are admissible. And on grounds which are independent of space and time, infinite numbers, and series in which no two terms are consecutive, must in any case be admitted. Consider, for example, all the fractions less than 1, arranged in order of magnitude. Between any two of them, there are others, for example, the arithmetical mean of the two. Thus no two fractions are consecutive, and the total number of them is infinite. It will be found that much of what Zeno says as regards the series of points on a line can be equally well applied to the series of fractions. And we cannot deny that there are fractions, so that two of the above ways of escape are closed to us. It follows that, if we are to solve the whole class of difficulties derivable from Zeno's by analogy, we must discover some tenable theory of infinite numbers. What, then, are the difficulties which, until the last thirty years, led philosophers to the belief that infinite numbers are impossible?
The difficulties of infinity are of two kinds, of which the first may be called sham, while the others involve, for their solution, a certain amount of new and not altogether easy thinking. The sham difficulties are those suggested by the etymology, and those suggested by confusion of the mathematical infinite with what philosophers impertinently call the “true” infinite. Etymologically, “infinite” should mean “having no end.” But in fact some infinite series have ends, some have not; while some collections are infinite without being serial, and can therefore not properly be regarded as either endless or having ends. The series of instants from any earlier one to any later one (both included) is infinite, but has two ends; the series of instants from the beginning of time to the present moment has one end, but is infinite. Kant, in his first antinomy, seems to hold that it is harder for the past to be infinite than for the future to be so, on the ground that the past is now completed, and that nothing infinite can be completed. It is very difficult to see how he can have imagined that there was any sense in this remark; but it seems most probable that he was thinking of the infinite as the “unended.” It is odd that he did not see that the future too has one end at the present, and is precisely on a level with the past. His regarding the two as different in this respect illustrates just that kind of slavery to time which, as we agreed in speaking of Parmenides, the true philosopher must learn to leave behind him.
The confusions introduced into the notions of philosophers by the so-called “true” infinite are curious. They see that this notion is not the same as the mathematical infinite, but they choose to believe that it is the notion which the mathematicians are vainly trying to reach. They therefore inform the mathematicians, kindly but firmly, that they are mistaken in adhering to the “false” infinite, since plainly the “true” infinite is something quite different. The reply to this is that what they call the “true” infinite is a notion totally irrelevant to the problem of the mathematical infinite, to which it has only a fanciful and verbal analogy. So remote is it that I do not propose to confuse the issue by even mentioning what the “true” infinite is. It is the “false” infinite that concerns us, and we have to show that the epithet “false” is undeserved.
There are, however, certain genuine difficulties in understanding the infinite, certain habits of mind derived from the consideration of finite numbers, and easily extended to infinite numbers under the mistaken notion that they represent logical necessities. For example, every number that we are accustomed to, except 0, has another number immediately before it, from which it results by adding 1; but the first infinite number does not have this property. The numbers before it form an infinite series, containing all the ordinary finite numbers, having no maximum, no last finite number, after which one little step would plunge us into the infinite. If it is assumed that the first infinite number is reached by a succession of small steps, it is easy to show that it is self-contradictory. The first infinite number is, in fact, beyond the whole unending series of finite numbers. “But,” it will be said, “there cannot be anything beyond the whole of an unending series.” This, we may point out, is the very principle upon which Zeno relies in the arguments of the race-course and the Achilles. Take the race-course: there is the moment when the runner still has half his distance to run, then the moment when he still has a quarter, then when he still has an eighth, and so on in a strictly unending series. Beyond the whole of this series is the moment when he reaches the goal. Thus there certainly can be something beyond the whole of an unending series. But it remains to show that this fact is only what might have been expected.
The difficulty, like most of the vaguer difficulties besetting the mathematical infinite, is derived, I think, from the more or less unconscious operation of the idea of counting. If you set to work to count the terms in an infinite collection, you will never have completed your task. Thus, in the case of the runner, if half, three-quarters, seven-eighths, and so on of the course were marked, and the runner was not allowed to pass any of the marks until the umpire said “Now,” then Zeno's conclusion would be true in practice, and he would never reach the goal.
But it is not essential to the existence of a collection, or even to knowledge and reasoning concerning it, that we should be able to pass its terms in review one by one. This may be seen in the case of finite collections; we can speak of “mankind” or “the human race,” though many of the individuals in this collection are not personally known to us. We can do this because we know of various characteristics which every individual has if he belongs to the collection, and not if he does not. And exactly the same happens in the case of infinite collections: they may be known by their characteristics although their terms cannot be enumerated. In this sense, an unending series may nevertheless form a whole, and there may be new terms beyond the whole of it.
Some purely arithmetical peculiarities of infinite numbers have also caused perplexity. For instance, an infinite number is not increased by adding one to it, or by doubling it. Such peculiarities have seemed to many to contradict logic, but in fact they only contradict confirmed mental habits. The whole difficulty of the subject lies in the necessity of thinking in an unfamiliar way, and in realising that many properties which we have thought inherent in number are in fact peculiar to finite numbers. If this is remembered, the positive theory of infinity, which will occupy the next lecture, will not be found so difficult as it is to those who cling obstinately to the prejudices instilled by the arithmetic which is learnt in childhood.