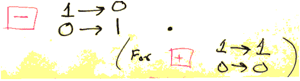by Wikipedia
November 5, 2017
NOTICE: THIS WORK MAY BE PROTECTED BY COPYRIGHT
YOU ARE REQUIRED TO READ THE COPYRIGHT NOTICE AT THIS LINK BEFORE YOU READ THE FOLLOWING WORK, THAT IS AVAILABLE SOLELY FOR PRIVATE STUDY, SCHOLARSHIP OR RESEARCH PURSUANT TO 17 U.S.C. SECTION 107 AND 108. IN THE EVENT THAT THE LIBRARY DETERMINES THAT UNLAWFUL COPYING OF THIS WORK HAS OCCURRED, THE LIBRARY HAS THE RIGHT TO BLOCK THE I.P. ADDRESS AT WHICH THE UNLAWFUL COPYING APPEARED TO HAVE OCCURRED. THANK YOU FOR RESPECTING THE RIGHTS OF COPYRIGHT OWNERS.
Nash in 2006
Born June 13, 1928
Bluefield, West Virginia, U.S.
Died May 23, 2015 (aged 86)
Monroe Township, Middlesex County, New Jersey, U.S.
Citizenship: United States
Alma mater: Carnegie Institute of Technology, B.S and M.S.
Princeton University Ph.D.
Known for: Nash equilibrium, Nash embedding theorem, Nash functions, Nash–Moser theorem
Spouse(s) Alicia Lopez-Harrison de Lardé (m. 1957–1963) (divorced); (m. 2001–2015) (their deaths)
Children: 2[1]
Awards: John von Neumann Theory Prize(1978), Nobel Memorial Prize in Economic Sciences (1994), Abel Prize (2015)
Scientific career
Fields: Mathematics, Economics
Institutions: Massachusetts Institute of Technology, Princeton University
Doctoral advisor: Albert W. Tucker
John Forbes Nash Jr. (June 13, 1928 – May 23, 2015) was an American mathematician who made fundamental contributions to game theory, differential geometry, and the study of partial differential equations.[2][3] Nash's work has provided insight into the factors that govern chance and decision-making inside complex systems found in everyday life.
His theories are widely used in economics. Serving as a Senior Research Mathematician at Princeton University during the latter part of his life, he shared the 1994 Nobel Memorial Prize in Economic Sciences with game theorists Reinhard Selten and John Harsanyi. In 2015, he also shared the Abel Prize with Louis Nirenberg for his work on nonlinear partial differential equations.
John Nash is the only person to be awarded both the Nobel Memorial Prize in Economic Sciences and the Abel Prize.
In 1959, Nash began showing clear signs of mental illness, and spent several years at psychiatric hospitals being treated for paranoid schizophrenia. After 1970, his condition slowly improved, allowing him to return to academic work by the mid-1980s.[4] His struggles with his illness and his recovery became the basis for Sylvia Nasar's biography, A Beautiful Mind, as well as a film of the same name starring Russell Crowe as Nash.[5][6][7]
On May 23, 2015, Nash and his wife Alicia were killed in a car crash while riding in a taxi on the New Jersey Turnpike.
Early life and education
Nash was born on June 13, 1928, in Bluefield, West Virginia. His father, John Forbes Nash, was an electrical engineer for the Appalachian Electric Power Company. His mother, Margaret Virginia (née Martin) Nash, had been a schoolteacher before she married. He was baptized in the Episcopal Church.[8] He had a younger sister, Martha (born November 16, 1930).
Nash attended kindergarten and public school, and he learned from books provided by his parents and grandparents.[9] Nash's parents pursued opportunities to supplement their son's education, and arranged for him to take advanced mathematics courses at a local community college during his final year of high school. He attended Carnegie Institute of Technology through a full benefit of the George Westinghouse Scholarship, initially majoring in chemical engineering. He switched to a chemistry major and eventually, at the advice of his teacher John Lighton Synge, to mathematics. After graduating in 1948 (at age 19) with both a B.S. and M.S. in mathematics, Nash accepted a scholarship to Princeton University, where he pursued further graduate studies in mathematics.[9]
Nash's adviser and former Carnegie professor Richard Duffin wrote a letter of recommendation for Nash's entrance to Princeton stating, "He is a mathematical genius."[10][11]Nash was accepted at Harvard University. However, the chairman of the mathematics department at Princeton, Solomon Lefschetz, offered him the John S. Kennedy fellowship, convincing Nash that Princeton valued him more.[12] Further, he considered Princeton more favorably because of its proximity to his family in Bluefield.[9] At Princeton, he began work on his equilibrium theory, later known as the Nash equilibrium.
Major contributions

Nash in November 2006 at a game theory conference in Cologne, Germany
Game theory
Nash earned a Ph.D. degree in 1950 with a 28-page dissertation on non-cooperative games.[13][14]
The thesis, written under the supervision of doctoral advisor Albert W. Tucker, contained the definition and properties of the Nash equilibrium, a crucial concept in non-cooperative games. It won Nash the Nobel Memorial Prize in Economic Sciences in 1994.
Publications authored by Nash relating to the concept are in the following papers :
• Nash, John Forbes (1950). "Equilibrium Points in N-person Games". Proceedings of the National Academy of Sciences of the United States of America. 36 (1): 48–49. doi:10.1073/pnas.36.1.48. MR 0031701. PMC 1063129 . PMID 16588946.
• Nash, John Forbes (1950). "The Bargaining Problem" (PDF). Econometrica. 18 (2): 155–62. doi:10.2307/1907266. JSTOR 1907266. MR 0035977.
• Nash, John Forbes (1951). "Non-cooperative Games" (PDF). Annals of Mathematics. 54 (2): 286–95. doi:10.2307/1969529. JSTOR 1969529. MR 0043432.
• Nash, John Forbes (1953). "Two-person Cooperative Games" (PDF). Econometrica. 21 (1): 128–40. doi:10.2307/1906951. MR 0053471.
Other mathematics
Nash did groundbreaking work in the area of real algebraic geometry:
• Nash, John Forbes (1952). "Real algebraic manifolds". Annals of Mathematics. 56 (3): 405–21. doi:10.2307/1969649. JSTOR 1969649. MR 0050928. See "Proc. Internat. Congr. Math". AMS. 1952: 516–17.
His work in mathematics includes the Nash embedding theorem, which shows that every abstract Riemannian manifold can be isometrically realized as a submanifold of Euclidean space. He also made significant contributions to the theory of nonlinear parabolic partial differential equations and to singularity theory.
In the introduction of the book Open Problems in Mathematics that John Nash edited jointly with Michael Th. Rassias in 2014–2015, Mikhail Leonidovich Gromov writes about Nash's work:
Nash was solving classical mathematical problems, difficult problems, something that nobody else was able to do, not even to imagine how to do it. ... But what Nash discovered in the course of his constructions of isometric embeddings is far from 'classical' — it is something that brings about a dramatic alteration of our understanding of the basic logic of analysis and differential geometry. Judging from the classical perspective, what Nash has achieved in his papers is as impossible as the story of his life ... [H]is work on isometric immersions ... opened a new world of mathematics that stretches in front of our eyes in yet unknown directions and still waits to be explored.[15]
John Milnor gives a list of 21 publications.[16]
In the Nash biography A Beautiful Mind, author Sylvia Nasar explains that Nash was working on proving Hilbert's nineteenth problem, a theorem involving elliptic partial differential equations when, in 1956, he suffered a severe disappointment. He learned that an Italian mathematician, Ennio de Giorgi, had published a proof just months before Nash achieved his proof. Each took different routes to get to their solutions. The two mathematicians met each other at the Courant Institute of Mathematical Sciences of New York University during the summer of 1956. It has been speculated that if only one had solved the problem, he would have been given the Fields Medal for the proof.[9]
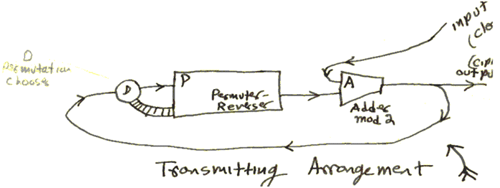
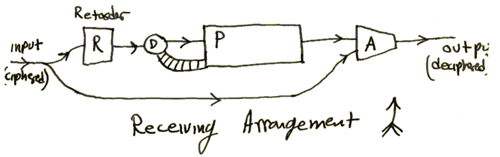
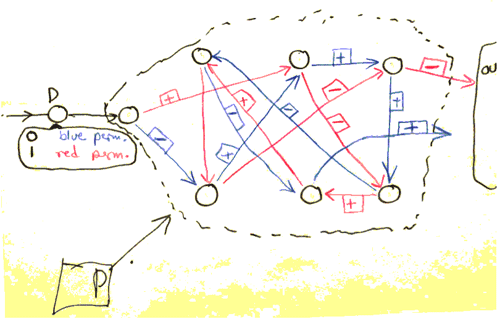
In 2011, the National Security Agency declassified letters written by Nash in the 1950s, in which he had proposed a new encryption–decryption machine.[17] The letters show that Nash had anticipated many concepts of modern cryptography, which are based on computational hardness.[18]
Mental illness
Nash's mental illness first began to manifest in the form of paranoia; his wife later describing his behavior as erratic. Nash seemed to believe that all men who wore red ties were part of a communist conspiracy against him; Nash mailed letters to embassies in Washington, D.C., declaring that they were establishing a government.[4][19] Nash's psychological issues crossed into his professional life when he gave an American Mathematical Society lecture at Columbia University in 1959. Originally intended to present proof of the Riemann hypothesis, the lecture was incomprehensible. Colleagues in the audience immediately realized that something was wrong.[20]
He was admitted to McLean Hospital in April 1959, staying through May of the same year. There, he was diagnosed with paranoid schizophrenia. According to the Diagnostic and Statistical Manual of Mental Disorders, or DSM, a person suffering from the disorder is typically dominated by relatively stable, often paranoid, fixed beliefs that are either false, over-imaginative or unrealistic, and usually accompanied by experiences of seemingly real perception of something not actually present. Further signs are marked particularly by auditory and perceptional disturbances, a lack of motivation for life, and mild clinical depression.[21][22]
Where is the CIA's headquarters? Is it in Langley or McLean, Virginia?
by cia.gov
Accessed November 5, 2017
Technically, you could say CIA headquarters is in both. "Langley" is the name of the McLean neighborhood in which the CIA resides.
The town of McLean was founded in 1910, but before then, the area where CIA Headquarters is located was known as Langley.
In 1719, Thomas Lee purchased a tract of land from the sixth Lord Fairfax (for whom Fairfax County, the county in which McLean is located, was named), and he named it "Langley" after his ancestral home in England. Though Lee never lived on the land, the Langley area soon became home to many European settlers. A few were wealthy people whom England had granted land, and they established large plantations in the area.
During the War of 1812, President James Madison and his wife Dolley fled the British siege of Washington to the safety of family and friends in Langley. Langley was a Union stronghold in Virginia, a southern state, during the Civil War and had two forts, Camp Griffin and Camp Pierpont, which housed soldiers who helped protect Washington.
With the building of the Great Falls & Old Dominion Railroad, 1903 was a defining year for Langley. John McLean, president of Washington Gas Light Company and, later, editor of the Washington Post, and Senator Stephen B. Elkins of West Virginia collaborated on construction of a railroad which would bring vacationing Washingtonians to nearby Great Falls and provide people who worked in Washington the choice of living outside of the city. In 1906, the railroad began operating, and the population of Langley and nearby Lewinsville quickly grew. In 1910, the post offices of these towns closed and, named for the man who helped the area grow, a new post office named "McLean" was opened. In 1959, the Federal government broke ground for the Central Intelligence Agency headquarters. Construction was completed in 1961, adding another chapter to McLean's long history.
Despite the name change in 1910, the name "Langley" still lingers to describe the McLean neighborhood where the CIA is located.
Source: Ellis, Rafaela "A Community Called McLean"
In 1961, Nash was admitted to the New Jersey State Hospital at Trenton.[23] Over the next nine years, he spent periods in psychiatric hospitals, where he received both antipsychotic medications and insulin shock therapy.[22][24][25]
Although he sometimes took prescribed medication, Nash later wrote that he did so only under pressure. After 1970, he was never committed to a hospital again, and he refused any further medication. According to Nash, the film A Beautiful Mind inaccurately implied he was taking what were the new atypical antipsychotics of the time period. He attributed the depiction to the screenwriter who was worried about the film encouraging people with the disorder to stop taking their medication.[26] Journalist Robert Whitaker wrote an article suggesting recovery from illnesses like Nash's can be hindered by such drugs.[27]
Nash felt psychotropic drugs were overrated and that the adverse effects were not given enough consideration once someone was deemed mentally ill.[28][29][30] According to Sylvia Nasar, author of the book A Beautiful Mind, on which the movie was based, Nash recovered gradually with the passage of time. Encouraged by his then former wife, de Lardé, Nash worked in a communitarian setting where his eccentricities were accepted. De Lardé said of Nash, "it's just a question of living a quiet life."[4]
Nash dated the start of what he termed "mental disturbances" to the early months of 1959, when his wife was pregnant. He described a process of change "from scientific rationality of thinking into the delusional thinking characteristic of persons who are psychiatrically diagnosed as 'schizophrenic' or 'paranoid schizophrenic'".[9] For Nash, this included seeing himself as a messenger or having a special function of some kind, of having supporters and opponents and hidden schemers, along with a feeling of being persecuted and searching for signs representing divine revelation.[31] Nash suggested his delusional thinking was related to his unhappiness, his desire to feel important and be recognized, and his characteristic way of thinking, saying, "I wouldn't have had good scientific ideas if I had thought more normally." He also said, "If I felt completely pressureless I don't think I would have gone in this pattern".[32] He did not draw a categorical distinction between schizophrenia and bipolar disorder.[33] Nash reported he did not hear voices until around 1964, and later engaged in a process of consciously rejecting them.[34] He further stated he was always taken to hospitals against his will. He only temporarily renounced his "dream-like delusional hypotheses" after being in a hospital long enough to decide he would superficially conform — to behave normally or to experience "enforced rationality". Only gradually on his own did he "intellectually reject" some of the "delusionally influenced" and "politically oriented" thinking as a waste of effort. By 1995, however, even though he was "thinking rationally again in the style that is characteristic of scientists," he said he felt more limited.[9][35]
Nash wrote in 1994:
I spent times of the order of five to eight months in hospitals in New Jersey, always on an involuntary basis and always attempting a legal argument for release. And it did happen that when I had been long enough hospitalized that I would finally renounce my delusional hypotheses and revert to thinking of myself as a human of more conventional circumstances and return to mathematical research. In these interludes of, as it were, enforced rationality, I did succeed in doing some respectable mathematical research. Thus there came about the research for "Le problème de Cauchy pour les équations différentielles d'un fluide général"; the idea that Prof. [Heisuke] Hironaka called "the Nash blowing-up transformation"; and those of "Arc Structure of Singularities" and "Analyticity of Solutions of Implicit Function Problems with Analytic Data".
But after my return to the dream-like delusional hypotheses in the later 60s I became a person of delusionally influenced thinking but of relatively moderate behavior and thus tended to avoid hospitalization and the direct attention of psychiatrists.
Thus further time passed. Then gradually I began to intellectually reject some of the delusionally influenced lines of thinking which had been characteristic of my orientation. This began, most recognizably, with the rejection of politically oriented thinking as essentially a hopeless waste of intellectual effort. So at the present time I seem to be thinking rationally again in the style that is characteristic of scientists.[9]
Recognition and later career

Nash pictured in 2011
In 1978, Nash was awarded the John von Neumann Theory Prize for his discovery of non-cooperative equilibria, now called Nash Equilibria. He won the Leroy P. Steele Prize in 1999.
In 1994, he received the Nobel Memorial Prize in Economic Sciences (along with John Harsanyi and Reinhard Selten) as a result of his game theory work as a Princeton graduate student. In the late 1980s, Nash had begun to use email to gradually link with working mathematicians who realized that he was the John Nash and that his new work had value. They formed part of the nucleus of a group that contacted the Bank of Sweden's Nobel award committee and were able to vouch for Nash's mental health ability to receive the award in recognition of his early work.[36]
Nash's later work involved ventures in advanced game theory, including partial agency, which show that, as in his early career, he preferred to select his own path and problems. Between 1945 and 1996, he published 23 scientific studies.
Nash has suggested hypotheses on mental illness. He has compared not thinking in an acceptable manner, or being "insane" and not fitting into a usual social function, to being "on strike" from an economic point of view. He advanced views in evolutionary psychology about the value of human diversity and the potential benefits of apparently nonstandard behaviors or roles.[37]
Nash developed work on the role of money in society. Within the framing theorem that people can be so controlled and motivated by money that they may not be able to reason rationally about it, he criticized interest groups that promote quasi-doctrines based on Keynesian economics that permit manipulative short-term inflation and debt tactics that ultimately undermine currencies. He suggested a global "industrial consumption price index" system that would support the development of more "ideal money" that people could trust rather than more unstable "bad money". He noted that some of his thinking parallels economist and political philosopher Friedrich Hayek's thinking regarding money and a nontypical viewpoint of the function of the authorities.[38][39]
Nash received an honorary degree, Doctor of Science and Technology, from Carnegie Mellon University in 1999, an honorary degree in economics from the University of Naples Federico II on March 19, 2003,[40] an honorary doctorate in economics from the University of Antwerp in April 2007, an honorary doctorate of science from the City University of Hong Kong on November 8, 2011,[1] and was keynote speaker at a conference on game theory.[41] He has also been a prolific guest speaker at a number of world-class events, such as the Warwick Economics Summit in 2005 held at the University of Warwick. In 2012, he was elected as a fellow of the American Mathematical Society.[42] On May 19, 2015, a few days before his death, Nash, along with Louis Nirenberg, was awarded the 2015 Abel Prize by King Harald V of Norway at a ceremony in Oslo.[43]
Personal life
In 1951, Nash was hired by the Massachusetts Institute of Technology (MIT) as a C. L. E. Moore instructor in the mathematics faculty. About a year later, Nash began a relationship in Massachusetts with Eleanor Stier, a nurse he met while admitted as a patient. They had a son, John David Stier,[1] but Nash left Stier when she told him of her pregnancy.[44] The film based on Nash's life, A Beautiful Mind, was criticized during the run-up to the 2002 Oscars for omitting this aspect of his life. He was said to have abandoned her based on her social status, which he thought to have been beneath his.[45]
In Santa Monica, California in 1954, while in his 20s, Nash was arrested for indecent exposure in a sting operation targeting homosexual men.[46] Although the charges were dropped, he was stripped of his top-secret security clearance and fired from RAND Corporation, where he had worked as a consultant.[47]
In Jan 55 Mr. Nash offered general remarks on cryptography and requested valuation of descriptive material which he had forwarded through Rand Corp. The Material was not received from Rand Corp. Dr. Campaigne received a letter from Mr. Nash enclosing a copy of the letter (5 Apr 54) from Rand which transmitted this material to NSA. This material was found in R/D files.
-- M.A. Lyons, 4128/60372/rwb
Not long after breaking up with Stier, Nash met Alicia Lardé Lopez-Harrison (January 1, 1933 – May 23, 2015), a naturalized U.S. citizen from El Salvador. Lardé graduated from MIT, having majored in physics.[9] They married in February 1957; although Nash was an atheist, the ceremony was performed in an Episcopal church.[48][49]
In 1958, Nash earned a tenured position at MIT, and his first signs of mental illness were evident in early 1959. At this time, his wife was pregnant with their first child. He resigned his position as a member of the MIT mathematics faculty in the spring of 1959[9] and his wife had him admitted to McLean Hospital for treatment of schizophrenia that same year. Their son, John Charles Martin Nash, was born soon afterward. The child was not named for a year[1] because his wife felt Nash should have a say in the name given to the boy. Due to the stress of dealing with his illness, Nash and de Lardé divorced in 1963. After his final hospital discharge in 1970, Nash lived in de Lardé's house as a boarder. This stability seemed to help him, and he learned how to consciously discard his paranoid delusions.[50] He stopped taking psychiatric medication and was allowed by Princeton to audit classes. He continued to work on mathematics and eventually he was allowed to teach again. In the 1990s, Lardé and Nash resumed their relationship, remarrying in 2001.
Death
On May 23, 2015, Nash and his wife were killed in a vehicle collision on the New Jersey Turnpike near Monroe Township, New Jersey. They had been on their way home from the airport after a visit to Norway, where Nash had received the Abel Prize, when their taxicab driver lost control of the vehicle and struck a guardrail. Both passengers were ejected from the car upon impact. State police revealed that it appeared neither passenger was wearing a seatbelt at the time of the collision.[51][52][53][54][55] At the time of his death, the 86-year-old Nash was a longtime resident of West Windsor Township, New Jersey.[56][57]
Following his death, obituaries appeared in scientific and popular media throughout the world.[58] In addition to their obituary for Nash,[59] The New York Times published an article containing quotes from Nash that had been assembled from media and other published sources. The quotes consisted of Nash's reflections on his life and achievements.[60]
Legacy
At Princeton, Nash became known as "The Phantom of Fine Hall"[61] (Princeton's mathematics center), a shadowy figure who would scribble arcane equations on blackboards in the middle of the night. He is referred to in a novel set at Princeton, The Mind-Body Problem, 1983, by Rebecca Goldstein.[4]
Sylvia Nasar's biography of Nash, A Beautiful Mind, was published in 1998. A film by the same name was released in 2001, directed by Ron Howard with Russell Crowe playing Nash; it won four Academy Awards, including Best Picture.
Awards
• 1978 – INFORMS John von Neumann Theory Prize
• 1994 – Nobel Memorial Prize in Economic Sciences
• 2010 – Double Helix Medal[62]
• 2015 – Abel Prize[63]
References
1. Suellentrop, Chris (2001-12-21). "A Real Number". Slate. Archived from the original on 2014-01-04. Retrieved 2015-05-28. A Beautiful Mind's John Nash is nowhere near as complicated as the real one.
2. Goode, Erica (May 24, 2015). "John F. Nash Jr., Math Genius Defined by a 'Beautiful Mind,' Dies at 86". The New York Times.
3. "John F. Nash Jr. and Louis Nirenberg share the Abel Prize". Abel Prize. March 25, 2015.
4. Nasar, Sylvia (November 13, 1994). "The Lost Years of a Nobel Laureate". The New York Times. Princeton, New Jersey. Retrieved May 6, 2014.
5. "Oscar race scrutinizes movies based on true stories". USA Today. March 6, 2002. Retrieved January 22, 2008.
6. "Academy Award Winners". USA Today. March 25, 2002. Retrieved August 30, 2008.
7. Yuhas, Daisy. "Throughout History, Defining Schizophrenia Has Remained A Challenge (Timeline)". Scientific American Mind. Retrieved March 2, 2013.
8. Nasar, Sylvia (1998). "Chapter One". A Beautiful Mind. Simon & Schuster. ISBN 0-684-81906-6. Archived from the original on December 5, 2000.
9. Nash, John (1995) "John F. Nash Jr. – Biographical"from Les Prix Nobel. The Nobel Prizes 1994, Editor Tore Frängsmyr, [Nobel Foundation], Stockholm, 1952,
10. "Nash recommendation letter" (PDF). p. 23.
11. Kuhn W, Harold; Nasar, Sylvia (eds.). "The Essential John Nash"(PDF). Princeton University Press. pp. Introduction, xi. Retrieved April 17, 2008.
12. Nasar (2011), pp. 46–7.
13. Nash, John F. (May 1950). "Non-Cooperative Games" (PDF). PhD thesis. Princeton University. Archived (PDF) from the original on May 24, 2015. Retrieved May 24, 2015.
14. Osborne, MJ (2004). An Introduction to Game Theory. Oxford, ENG: Oxford University Press. p. 23. ISBN 0-19-512895-8.
15. Nash, J. F.; Rassias, M. Th. (2016). Open Problems in Mathematics. Springer, New York. pp. xi–xiii.
16. John Nash and “A Beautiful Mind”, John Milnor, Notices of the AMS v.25 No. 10 pp. 1329–1332, November 1998]
17. "2012 Press Release – National Cryptologic Museum Opens New Exhibit on Dr. John Nash". National Security Agency. Retrieved February 25, 2012.
18. "John Nash's Letter to the NSA ; Turing's Invisible Hand". Retrieved February 25, 2012.
19. Nasar (2011), p. 251.
20. Sabbagh, Karl (2003). Dr. Riemann's Zeros. London: Atlantic Books. pp. 87–88. ISBN 1-84354-100-9.
21. "Brown University Didactic Readings: DSM-IV Schizophrenia (DSM-IV-TR #295.1–295.3, 295.90)" (PDF). Brown University. pp. 1–11. Retrieved June 1, 2015.
22. Nasar (2011), p. 32.
23. O'Connor, John J.; Robertson, Edmund F., "John Forbes Nash Jr.", MacTutor History of Mathematics archive, University of St Andrews.
24. Ebert, Roger (2002). Roger Ebert's Movie Yearbook 2003. Andrews McMeel Publishing. ISBN 978-0-7407-2691-0. Retrieved July 10, 2008.
25. Beam, Alex (2001). Gracefully Insane: The Rise and Fall of America's Premier Mental Hospital. PublicAffairs. ISBN 978-1-58648-161-2. Retrieved July 10, 2008.
26. Greihsel, Marika (September 1, 2004) John F. Nash Jr. – Interview. Nobel Foundation Interview, September 2004.
27. Whitaker, R. (March 4, 2002) "Mind drugs may hinder recovery". By Robert Whitaker USA Today 03/03/2002 – Updated 10:30 PM ET.
28. Nash, John "PBS Interview: Medication". 2002.
29. Nash, John "PBS Interview: Paths to Recovery". 2002.
30. Nash, John "PBS Interview: How does Recovery Happen?" 2002.
31. Nash, John "PBS Interview: Delusional Thinking". 2002.
32. Nash, John "PBS Interview: The Downward Spiral" 2002.
33. Nash, John (April 10, 2005) "Glimpsing inside a beautiful mind". Interview by Shane Hegarty. Schizophrenia.com.
34. Nash, John "PBS Interview: Hearing voices". 2002.
35. Nash, John "John Nash: My experience with mental illness". PBS Interview,2002.
36. "The Work of John Nash in Game Theory" (PDF). Nobel Seminar. 8 December 1994. Retrieved 29 May 2015.
37. Neubauer, David (June 1, 2007). "John Nash and a Beautiful Mind on Strike". Yahoo! Health. Archived from the original on April 21, 2008.
38. Nash, John (2002). "Ideal Money". Southern Economic Journal. 69(1): 4–11. doi:10.2307/1061553. JSTOR 1061553.
39. Zuckerman, Julia (April 27, 2005) "Nobel winner Nash critiques economic theory". The Brown Daily Herald. By JULIA ZUCKERMAN Wednesday, April 27, 2005
40. Capua, Patrizia (March 19, 2003). "Napoli, laurea a Nash il 'genio dei numeri'" (in Italian). la Repubblica.it.
41. "Nobel Laureate John Nash to Visit HK". http://www.china.org.cn. Retrieved 7 January 2017.
42. List of Fellows of the American Mathematical Society, retrieved February 24, 2013.
43. "Nash and Nirenberg received the Abel Prize from the King of Norway". The Norwegian Academy of Science and Letters. Retrieved May 24, 2015.
44. Goldstein, Scott (April 10, 2005) Eleanor Stier, 84; Brookline nurse had son with Nobel laureate mathematician John F. Nash Jr., Boston.com News.
45. Sutherland, John (March 18, 2002) "Beautiful mind, lousy character", The Guardian, March 18, 2002.
46. "John Nash, mathematician - obituary". The Telegraph. 24 May 2015. Retrieved 29 August 2016.
47. Nasar, Sylvia (March 25, 2002). "The sum of a man". The Guardian. Retrieved July 9, 2012. Contrary to widespread references to Nash's "numerous homosexual liaisons", he was not gay. While he had several emotionally intense relationships with other men when he was in his early 20s, I never interviewed anyone who claimed, much less provided evidence, that Nash ever had sex with another man. Nash was arrested in a police trap in a public lavatory in Santa Monica in 1954, at the height of the McCarthy hysteria. The military think-tank where he was a consultant, stripped him of his top-secret security clearance and fired him … The charge – indecent exposure – was dropped.
48. Nasar (2011), Chapter 17: Bad Boys, p. 143: "In this circle, Nash learned to make a virtue of necessity, styling himself self-consciously as a "free thinker." He announced that he was an atheist."
49. Nasar (2011), p. 212: "Nash, by then an atheist, balked at a Catholic ceremony. He would have been happy to get married in city hall."
50. David Goodstein, 'Mathematics to Madness, and Back', The New York Times, June 11, 1998
51. Ma, Myles (May 23, 2015). "Famed 'A Beautiful Mind' mathematician John Nash, wife killed in taxi crash, police say". NJ.com. Retrieved May 23, 2015.
52. "'A Beautiful Mind' mathematician John Nash, wife killed in crash". USA News. Retrieved May 24, 2015.
53. "'Beautiful Mind' mathematician John Nash killed in crash". BBC News. Retrieved May 24, 2015.
54. "Princeton mathematician John Nash and his wife, Alicia, are killed in a car accident". QUARTZ. Retrieved May 24, 2015.
55. "John Nash, mathematician who inspired 'A Beautiful Mind', killed in car crash". Reuters.com. Thomson Reuters. Retrieved May 24, 2015.
56. "John Forbes Nash May Lose N.J. Home". Associated Press. March 14, 2002. Retrieved February 22, 2011 – via HighBeam Research. West Windsor, N.J.: John Forbes Nash Jr., whose life is chronicled in the Oscar-nominated movie A Beautiful Mind, could lose his home if the township picks one of its proposals to replace a nearby bridge.
57. Sandoval, Edgar; Otis, Ginger Adams (May 25, 2015). "John Nash, 86, inspiration for the film 'A Beautiful Mind,' and wife die in car accident on New Jersey Turnpike: police". Daily News. Retrieved May 25,2015.
58. "John Nash, mathematician who inspired 'A Beautiful Mind,' killed in car crash". Reuters. 24 May 2017. Retrieved 7 January 2017.
59. Goode, Erica (May 24, 2015). "John F. Nash Jr., Math Genius Defined by a 'Beautiful Mind,' Dies at 86". The New York Times. Retrieved May 24, 2015.
60. "The Wisdom of a Beautiful Mind". The New York Times. May 24, 2015. Retrieved May 25, 2015.
61. Kwon, Ha Kyung (December 10, 2010). "Nash GS '50: 'The Phantom of Fine Hall'". The Daily Princetonian. Retrieved May 6, 2014.
62. "John F. Nash Jr. 2010 Honoree". Retrieved July 16, 2014.
63. "Nash receives Abel Prize for revered work in mathematics". Retrieved March 25, 2015.
Bibliography
• Acocella, Nicola and Di Bartolomeo, Giovanni (2006), ‘Tinbergen and Theil meet Nash: controllability in policy games’, in: ‘Economics Letters’, 90(2): 213–218.
• Acocella, Nicola and Di Bartolomeo, G. and Piacquadio, P.G. [2009], ‘Conflict of interest, (implicit) coalitions and Nash policy games’, in: ‘Economics Letters’, 105: 303–305.
• Nasar, Sylvia (1998). A Beautiful Mind. Simon and Schuster. ISBN 978-1-4391-2649-3.
• O'Connor, John J.; Robertson, Edmund F., "John Forbes Nash Jr.", MacTutor History of Mathematics archive, University of St Andrews.
Documentaries and video interviews[edit]
• "A Brilliant Madness" – a PBS American Experience documentary
• One on One – Professor John Nash with Riz Khan. Al Jazeera English, 2009-12-05 (part 1 on YouTube, part 2 on YouTube)