Chapter 29: The Solution of the Problem of Gravitation on the Basis of the General Principle of Relativity
If the reader has followed all our previous considerations, he will have no further difficulty in understanding the methods leading to the solution of the problem of gravitation.
We start off on a consideration of a Galileian domain, i.e. a domain in which there is no gravitational field relative to the Galileian reference-body K. The behaviour of measuring-rods and clocks with reference to K is known from the special theory of relativity, likewise the behaviour of "isolated" material points; the latter move uniformly and in straight lines.
Now let us refer this domain to a random Gauss coordinate system or to a "mollusc" as reference-body K1. Then with respect to K1 there is a gravitational field G (of a particular kind). We learn the behaviour of measuring-rods and clocks and also of freely-moving material points with reference to K1 simply by mathematical transformation. We interpret this behaviour as the behaviour of measuring-rods, docks and material points tinder the influence of the gravitational field G. Hereupon we introduce a hypothesis: that the influence of the gravitational field on measuringrods, clocks and freely-moving material points continues to take place according to the same laws, even in the case where the prevailing gravitational field is not derivable from the Galfleian special care, simply by means of a transformation of co-ordinates.
The next step is to investigate the space-time behaviour of the gravitational field G, which was derived from the Galileian special case simply by transformation of the coordinates. This behaviour is formulated in a law, which is always valid, no matter how the reference-body (mollusc) used in the description may be chosen.
This law is not yet the general law of the gravitational field, since the gravitational field under consideration is of a special kind. In order to find out the general law-of-field of gravitation we still require to obtain a generalisation of the law as found above. This can be obtained without caprice, however, by taking into consideration the following demands:
(a) The required generalisation must likewise satisfy the general postulate of relativity.
(b) If there is any matter in the domain under consideration, only its inertial mass, and thus according to Section 15 only its energy is of importance for its effect in exciting a field.
(c) Gravitational field and matter together must satisfy the law of the conservation of energy (and of impulse).
Finally, the general principle of relativity permits us to determine the influence of the gravitational field on the course of all those processes which take place according to known laws when a gravitational field is absent i.e. which have already been fitted into the frame of the special theory of relativity. In this connection we proceed in principle according to the method which has already been explained for measuring-rods, clocks and freely moving material points.
The theory of gravitation derived in this way from the general postulate of relativity excels not only in its beauty ; nor in removing the defect attaching to classical mechanics which was brought to light in Section 21; nor in interpreting the empirical law of the equality of inertial and gravitational mass ; but it has also already explained a result of observation in astronomy, against which classical mechanics is powerless.
If we confine the application of the theory to the case where the gravitational fields can be regarded as being weak, and in which all masses move with respect to the coordinate system with velocities which are small compared with the velocity of light, we then obtain as a first approximation the Newtonian theory. Thus the latter theory is obtained here without any particular assumption, whereas Newton had to introduce the hypothesis that the force of attraction between mutually attracting material points is inversely proportional to the square of the distance between them. If we increase the accuracy of the calculation, deviations from the theory of Newton make their appearance, practically all of which must nevertheless escape the test of observation owing to their smallness.
We must draw attention here to one of these deviations. According to Newton's theory, a planet moves round the sun in an ellipse, which would permanently maintain its position with respect to the fixed stars, if we could disregard the motion of the fixed stars themselves and the action of the other planets under consideration. Thus, if we correct the observed motion of the planets for these two influences, and if Newton's theory be strictly correct, we ought to obtain for the orbit of the planet an ellipse, which is fixed with reference to the fixed stars. This deduction, which can be tested with great accuracy, has been confirmed for all the planets save one, with the precision that is capable of being obtained by the delicacy of observation attainable at the present time. The sole exception is Mercury, the planet which lies nearest the sun. Since the time of Leverrier, it has been known that the ellipse corresponding to the orbit of Mercury, after it has been corrected for the influences mentioned above, is not stationary with respect to the fixed stars, but that it rotates exceedingly slowly in the plane of the orbit and in the sense of the orbital motion. The value obtained for this rotary movement of the orbital ellipse was 43 seconds of arc per century, an amount ensured to be correct to within a few seconds of arc. This effect can be explained by means of classical mechanics only on the assumption of hypotheses which have little probability, and which were devised solely for this purpose.
On the basis of the general theory of relativity, it is found that the ellipse of every planet round the sun must necessarily rotate in the manner indicated above ; that for all the planets, with the exception of Mercury, this rotation is too small to be detected with the delicacy of observation possible at the present time ; but that in the case of Mercury it must amount to 43 seconds of arc per century, a result which is strictly in agreement with observation.
Apart from this one, it has hitherto been possible to make only two deductions from the theory which admit of being tested by observation, to wit, the curvature of light rays by the gravitational field of the sun,1) and a displacement of the spectral lines of light reaching us from large stars, as compared with the corresponding lines for light produced in an analogous manner terrestrially (i.e. by the same kind of atom). 2) These two deductions from the theory have both been confirmed.
_______________
Notes:
1) First observed by Eddington and others in 1919. (Cf. Appendix III, pp. 126-129).
2) Established by Adams in 1924. (Cf. p. 132)
Relativity, The Special and General Theory
38 posts
• Page 4 of 4 • 1, 2, 3, 4
Re: Relativity, The Special and General Theory
Chapter 30
Part III
Considerations on the Universe as a Whole
Cosmological Difficulties of Newton's Theory
Part from the difficulty discussed in Section 21, there is a second fundamental difficulty attending classical celestial mechanics, which, to the best of my knowledge, was first discussed in detail by the astronomer Seeliger. If we ponder over the question as to how the universe, considered as a whole, is to be regarded, the first answer that suggests itself to us is surely this: As regards space (and time) the universe is infinite. There are stars everywhere, so that the density of matter, although very variable in detail, is nevertheless on the average everywhere the same. In other words: However far we might travel through space, we should find everywhere an attenuated swarm of fixed stars of approximately the same kind and density.
This view is not in harmony with the theory of Newton. The latter theory rather requires that the universe should have a kind of centre in which the density of the stars is a maximum, and that as we proceed outwards from this centre the group-density of the stars should diminish, until finally, at great distances, it is succeeded by an infinite region of emptiness. The stellar universe ought to be a finite island in the infinite ocean of space. 1)
This conception is in itself not very satisfactory. It is still less satisfactory because it leads to the result that the light emitted by the stars and also individual stars of the stellar system are perpetually passing out into infinite space, never to return, and without ever again coming into interaction with other objects of nature. Such a finite material universe would be destined to become gradually but systematically impoverished.
In order to escape this dilemma, Seeliger suggested a modification of Newton's law, in which he assumes that for great distances the force of attraction between two masses diminishes more rapidly than would result from the inverse square law. In this way it is possible for the mean density of matter to be constant everywhere, even to infinity, without infinitely large gravitational fields being produced. We thus free ourselves from the distasteful conception that the material universe ought to possess something of the nature of a centre. Of course we purchase our emancipation from the fundamental difficulties mentioned, at the cost of a modification and complication of Newton's law which has neither empirical nor theoretical foundation. We can imagine innumerable laws which would serve the same purpose, without our being able to state a reason why one of them is to be preferred to the others ; for any one of these laws would be founded just as little on more general theoretical principles as is the law of Newton.
_______________
Notes:
1) Proof — According to the theory of Newton, the number of "lines of force" which come from infinity and terminate in a mass m is proportional to the mass m. If, on the average, the Mass density p0 is constant throughout tithe universe, then a sphere of volume V will enclose the average man p0V. Thus the number of lines of force passing through the surface F of the sphere into its interior is proportional to p0 V. For unit area of the surface of the sphere the number of lines of force which enters the sphere is thus proportional to p0 V/F or to p0R. Hence the intensity of the field at the surface would ultimately become infinite with increasing radius R of the sphere, which is impossible.
Part III
Considerations on the Universe as a Whole
Cosmological Difficulties of Newton's Theory
Part from the difficulty discussed in Section 21, there is a second fundamental difficulty attending classical celestial mechanics, which, to the best of my knowledge, was first discussed in detail by the astronomer Seeliger. If we ponder over the question as to how the universe, considered as a whole, is to be regarded, the first answer that suggests itself to us is surely this: As regards space (and time) the universe is infinite. There are stars everywhere, so that the density of matter, although very variable in detail, is nevertheless on the average everywhere the same. In other words: However far we might travel through space, we should find everywhere an attenuated swarm of fixed stars of approximately the same kind and density.
This view is not in harmony with the theory of Newton. The latter theory rather requires that the universe should have a kind of centre in which the density of the stars is a maximum, and that as we proceed outwards from this centre the group-density of the stars should diminish, until finally, at great distances, it is succeeded by an infinite region of emptiness. The stellar universe ought to be a finite island in the infinite ocean of space. 1)
This conception is in itself not very satisfactory. It is still less satisfactory because it leads to the result that the light emitted by the stars and also individual stars of the stellar system are perpetually passing out into infinite space, never to return, and without ever again coming into interaction with other objects of nature. Such a finite material universe would be destined to become gradually but systematically impoverished.
In order to escape this dilemma, Seeliger suggested a modification of Newton's law, in which he assumes that for great distances the force of attraction between two masses diminishes more rapidly than would result from the inverse square law. In this way it is possible for the mean density of matter to be constant everywhere, even to infinity, without infinitely large gravitational fields being produced. We thus free ourselves from the distasteful conception that the material universe ought to possess something of the nature of a centre. Of course we purchase our emancipation from the fundamental difficulties mentioned, at the cost of a modification and complication of Newton's law which has neither empirical nor theoretical foundation. We can imagine innumerable laws which would serve the same purpose, without our being able to state a reason why one of them is to be preferred to the others ; for any one of these laws would be founded just as little on more general theoretical principles as is the law of Newton.
_______________
Notes:
1) Proof — According to the theory of Newton, the number of "lines of force" which come from infinity and terminate in a mass m is proportional to the mass m. If, on the average, the Mass density p0 is constant throughout tithe universe, then a sphere of volume V will enclose the average man p0V. Thus the number of lines of force passing through the surface F of the sphere into its interior is proportional to p0 V. For unit area of the surface of the sphere the number of lines of force which enters the sphere is thus proportional to p0 V/F or to p0R. Hence the intensity of the field at the surface would ultimately become infinite with increasing radius R of the sphere, which is impossible.
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Chapter 31: The Possibility of a "Finite" and yet "Unbounded" Universe
But speculations on the structure of the universe also move in quite another direction. The development of non-Euclidean geometry led to the recognition of the fact, that we can cast doubt on the infiniteness of our space without coming into conflict with the laws of thought or with experience (Riemann, Helmholtz). These questions have already been treated in detail and with unsurpassable lucidity by Helmholtz and Poincaré, whereas I can only touch on them briefly here.
In the first place, we imagine an existence in two dimensional space. Flat beings with flat implements, and in particular flat rigid measuring-rods, are free to move in a plane. For them nothing exists outside of this plane: that which they observe to happen to themselves and to their flat " things " is the all-inclusive reality of their plane. In particular, the constructions of plane Euclidean geometry can be carried out by means of the rods e.g. the lattice construction, considered in Section 24. In contrast to ours, the universe of these beings is two-dimensional; but, like ours, it extends to infinity. In their universe there is room for an infinite number of identical squares made up of rods, i.e. its volume (surface) is infinite. If these beings say their universe is " plane," there is sense in the statement, because they mean that they can perform the constructions of plane Euclidean geometry with their rods. In this connection the individual rods always represent the same distance, independently of their position.
Let us consider now a second two-dimensional existence, but this time on a spherical surface instead of on a plane. The flat beings with their measuring-rods and other objects fit exactly on this surface and they are unable to leave it. Their whole universe of observation extends exclusively over the surface of the sphere. Are these beings able to regard the geometry of their universe as being plane geometry and their rods withal as the realisation of " distance " ? They cannot do this. For if they attempt to realise a straight line, they will obtain a curve, which we " three-dimensional beings " designate as a great circle, i.e. a self-contained line of definite finite length, which can be measured up by means of a measuring-rod. Similarly, this universe has a finite area that can be compared with the area, of a square constructed with rods. The great charm resulting from this consideration lies in the recognition of the fact that the universe of these beings is finite and yet has no limits.
But the spherical-surface beings do not need to go on a world-tour in order to perceive that they are not living in a Euclidean universe. They can convince themselves of this on every part of their " world," provided they do not use too small a piece of it. Starting from a point, they draw " straight lines " (arcs of circles as judged in three dimensional space) of equal length in all directions. They will call the line joining the free ends of these lines a " circle." For a plane surface, the ratio of the circumference of a circle to its diameter, both lengths being measured with the same rod, is, according to Euclidean geometry of the plane, equal to a constant value π, which is independent of the diameter of the circle. On their spherical surface our flat beings would find for this ratio the value
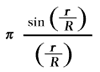
i.e. a smaller value than π, the difference being the more considerable, the greater is the radius of the circle in comparison with the radius R of the " world-sphere." By means of this relation the spherical beings can determine the radius of their universe (" world "), even when only a relatively small part of their worldsphere is available for their measurements. But if this part is very small indeed, they will no longer be able to demonstrate that they are on a spherical " world " and not on a Euclidean plane, for a small part of a spherical surface differs only slightly from a piece of a plane of the same size.
Thus if the spherical surface beings are living on a planet of which the solar system occupies only a negligibly small part of the spherical universe, they have no means of determining whether they are living in a finite or in an infinite universe, because the " piece of universe " to which they have access is in both cases practically plane, or Euclidean. It follows directly from this discussion, that for our sphere-beings the circumference of a circle first increases with the radius until the " circumference of the universe " is reached, and that it thenceforward gradually decreases to zero for still further increasing values of the radius. During this process the area of the circle continues to increase more and more, until finally it becomes equal to the total area of the whole " world-sphere."
Perhaps the reader will wonder why we have placed our " beings " on a sphere rather than on another closed surface. But this choice has its justification in the fact that, of all closed surfaces, the sphere is unique in possessing the property that all points on it are equivalent. I admit that the ratio of the circumference c of a circle to its radius r depends on r, but for a given value of r it is the same for all points of the "worldsphere"; in other words, the "world-sphere" is a "surface of constant curvature."
To this two-dimensional sphere-universe there is a three-dimensional analogy, namely, the three-dimensional spherical space which was discovered by Riemann. its points are likewise all equivalent. It possesses a finite volume, which is determined by its "radius" (2π2R3). Is it possible to imagine a spherical space? To imagine a space means nothing else than that we imagine an epitome of our " space " experience, i.e. of experience that we can have in the movement of " rigid " bodies. In this sense we can imagine a spherical space.
Suppose we draw lines or stretch strings in all directions from a point, and mark off from each of these the distance r with a measuring-rod. All the free end-points of these lengths lie on a spherical surface. We can specially measure up the area (F) of this surface by means of a square made up of measuring-rods. If the universe is Euclidean, then F = 4πR2 ; if it is spherical, then F is always less than 4πR2. With increasing values of r, F increases from zero up to a maximum value which is determined by the " world-radius," but for still further increasing values of r, the area gradually diminishes to zero. At first, the straight lines which radiate from the starting point diverge farther and farther from one another, but later they approach each other, and finally they run together again at a "counter-point" to the starting point. Under such conditions they have traversed the whole spherical space. It is easily seen that the three-dimensional spherical space is quite analogous to the two-dimensional spherical surface. It is finite (i.e. of finite volume), and has no bounds.
It may be mentioned that there is yet another kind of curved space: " elliptical space." It can be regarded as a curved space in which the two " counter-points " are identical (indistinguishable from each other). An elliptical universe can thus be considered to some extent as a curved universe possessing central symmetry.
It follows from what has been said, that closed spaces without limits are conceivable. From amongst these, the spherical space (and the elliptical) excels in its simplicity, since all points on it are equivalent. As a result of this discussion, a most interesting question arises for astronomers and physicists, and that is whether the universe in which we live is infinite, or whether it is finite in the manner of the spherical universe. Our experience is far from being sufficient to enable us to answer this question. But the general theory of relativity permits of our answering it with a modulate degree of certainty, and in this connection the difficulty mentioned in Section 30 finds its solution.
But speculations on the structure of the universe also move in quite another direction. The development of non-Euclidean geometry led to the recognition of the fact, that we can cast doubt on the infiniteness of our space without coming into conflict with the laws of thought or with experience (Riemann, Helmholtz). These questions have already been treated in detail and with unsurpassable lucidity by Helmholtz and Poincaré, whereas I can only touch on them briefly here.
In the first place, we imagine an existence in two dimensional space. Flat beings with flat implements, and in particular flat rigid measuring-rods, are free to move in a plane. For them nothing exists outside of this plane: that which they observe to happen to themselves and to their flat " things " is the all-inclusive reality of their plane. In particular, the constructions of plane Euclidean geometry can be carried out by means of the rods e.g. the lattice construction, considered in Section 24. In contrast to ours, the universe of these beings is two-dimensional; but, like ours, it extends to infinity. In their universe there is room for an infinite number of identical squares made up of rods, i.e. its volume (surface) is infinite. If these beings say their universe is " plane," there is sense in the statement, because they mean that they can perform the constructions of plane Euclidean geometry with their rods. In this connection the individual rods always represent the same distance, independently of their position.
Let us consider now a second two-dimensional existence, but this time on a spherical surface instead of on a plane. The flat beings with their measuring-rods and other objects fit exactly on this surface and they are unable to leave it. Their whole universe of observation extends exclusively over the surface of the sphere. Are these beings able to regard the geometry of their universe as being plane geometry and their rods withal as the realisation of " distance " ? They cannot do this. For if they attempt to realise a straight line, they will obtain a curve, which we " three-dimensional beings " designate as a great circle, i.e. a self-contained line of definite finite length, which can be measured up by means of a measuring-rod. Similarly, this universe has a finite area that can be compared with the area, of a square constructed with rods. The great charm resulting from this consideration lies in the recognition of the fact that the universe of these beings is finite and yet has no limits.
But the spherical-surface beings do not need to go on a world-tour in order to perceive that they are not living in a Euclidean universe. They can convince themselves of this on every part of their " world," provided they do not use too small a piece of it. Starting from a point, they draw " straight lines " (arcs of circles as judged in three dimensional space) of equal length in all directions. They will call the line joining the free ends of these lines a " circle." For a plane surface, the ratio of the circumference of a circle to its diameter, both lengths being measured with the same rod, is, according to Euclidean geometry of the plane, equal to a constant value π, which is independent of the diameter of the circle. On their spherical surface our flat beings would find for this ratio the value
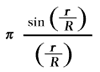
i.e. a smaller value than π, the difference being the more considerable, the greater is the radius of the circle in comparison with the radius R of the " world-sphere." By means of this relation the spherical beings can determine the radius of their universe (" world "), even when only a relatively small part of their worldsphere is available for their measurements. But if this part is very small indeed, they will no longer be able to demonstrate that they are on a spherical " world " and not on a Euclidean plane, for a small part of a spherical surface differs only slightly from a piece of a plane of the same size.
Thus if the spherical surface beings are living on a planet of which the solar system occupies only a negligibly small part of the spherical universe, they have no means of determining whether they are living in a finite or in an infinite universe, because the " piece of universe " to which they have access is in both cases practically plane, or Euclidean. It follows directly from this discussion, that for our sphere-beings the circumference of a circle first increases with the radius until the " circumference of the universe " is reached, and that it thenceforward gradually decreases to zero for still further increasing values of the radius. During this process the area of the circle continues to increase more and more, until finally it becomes equal to the total area of the whole " world-sphere."
Perhaps the reader will wonder why we have placed our " beings " on a sphere rather than on another closed surface. But this choice has its justification in the fact that, of all closed surfaces, the sphere is unique in possessing the property that all points on it are equivalent. I admit that the ratio of the circumference c of a circle to its radius r depends on r, but for a given value of r it is the same for all points of the "worldsphere"; in other words, the "world-sphere" is a "surface of constant curvature."
To this two-dimensional sphere-universe there is a three-dimensional analogy, namely, the three-dimensional spherical space which was discovered by Riemann. its points are likewise all equivalent. It possesses a finite volume, which is determined by its "radius" (2π2R3). Is it possible to imagine a spherical space? To imagine a space means nothing else than that we imagine an epitome of our " space " experience, i.e. of experience that we can have in the movement of " rigid " bodies. In this sense we can imagine a spherical space.
Suppose we draw lines or stretch strings in all directions from a point, and mark off from each of these the distance r with a measuring-rod. All the free end-points of these lengths lie on a spherical surface. We can specially measure up the area (F) of this surface by means of a square made up of measuring-rods. If the universe is Euclidean, then F = 4πR2 ; if it is spherical, then F is always less than 4πR2. With increasing values of r, F increases from zero up to a maximum value which is determined by the " world-radius," but for still further increasing values of r, the area gradually diminishes to zero. At first, the straight lines which radiate from the starting point diverge farther and farther from one another, but later they approach each other, and finally they run together again at a "counter-point" to the starting point. Under such conditions they have traversed the whole spherical space. It is easily seen that the three-dimensional spherical space is quite analogous to the two-dimensional spherical surface. It is finite (i.e. of finite volume), and has no bounds.
It may be mentioned that there is yet another kind of curved space: " elliptical space." It can be regarded as a curved space in which the two " counter-points " are identical (indistinguishable from each other). An elliptical universe can thus be considered to some extent as a curved universe possessing central symmetry.
It follows from what has been said, that closed spaces without limits are conceivable. From amongst these, the spherical space (and the elliptical) excels in its simplicity, since all points on it are equivalent. As a result of this discussion, a most interesting question arises for astronomers and physicists, and that is whether the universe in which we live is infinite, or whether it is finite in the manner of the spherical universe. Our experience is far from being sufficient to enable us to answer this question. But the general theory of relativity permits of our answering it with a modulate degree of certainty, and in this connection the difficulty mentioned in Section 30 finds its solution.
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Chapter 32: The Structure of Space According to the General Theory of Relativity
According to the general theory of relativity, the geometrical properties of space are not independent, but they are determined by matter. Thus we can draw conclusions about the geometrical structure of the universe only if we base our considerations on the state of the matter as being something that is known. We know from experience that, for a suitably chosen co-ordinate system, the velocities of the stars are small as compared with the velocity of transmission of light. We can thus as a rough approximation arrive at a conclusion as to the nature of the universe as a whole, if we treat the matter as being at rest.
We already know from our previous discussion that the behaviour of measuring-rods and clocks is influenced by gravitational fields, i.e. by the distribution of matter. This in itself is sufficient to exclude the possibility of the exact validity of Euclidean geometry in our universe. But it is conceivable that our universe differs only slightly from a Euclidean one, and this notion seems all the more probable, since calculations show that the metrics of surrounding space is influenced only to an exceedingly small extent by masses even of the magnitude of our sun. We might imagine that, as regards geometry, our universe behaves analogously to a surface which is irregularly curved in its individual parts, but which nowhere departs appreciably from a plane: something like the rippled surface of a lake. Such a universe might fittingly be called a quasi-Euclidean universe. As regards its space it would be infinite. But calculation shows that in a quasi-Euclidean universe the average density of matter would necessarily be nil. Thus such a universe could not be inhabited by matter everywhere ; it would present to us that unsatisfactory picture which we portrayed in Section 30.
If we are to have in the universe an average density of matter which differs from zero, however small may be that difference, then the universe cannot be quasi-Euclidean. On the contrary, the results of calculation indicate that if matter be distributed uniformly, the universe would necessarily be spherical (or elliptical). Since in reality the detailed distribution of matter is not uniform, the real universe will deviate in individual parts from the spherical, i.e. the universe will be quasi-spherical. But it will be necessarily finite. In fact, the theory supplies us with a simple connection 1) between the space-expanse of the universe and the average density of matter in it.
_______________
Notes:
1) For the radius R of the universe we obtain the equation
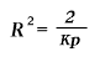
The use of the C.G.S. system in this equation gives 2/k = 1.08.1027; p is the average density of the matter and k is a constant connected with the Newtonian constant of gravitation.
According to the general theory of relativity, the geometrical properties of space are not independent, but they are determined by matter. Thus we can draw conclusions about the geometrical structure of the universe only if we base our considerations on the state of the matter as being something that is known. We know from experience that, for a suitably chosen co-ordinate system, the velocities of the stars are small as compared with the velocity of transmission of light. We can thus as a rough approximation arrive at a conclusion as to the nature of the universe as a whole, if we treat the matter as being at rest.
We already know from our previous discussion that the behaviour of measuring-rods and clocks is influenced by gravitational fields, i.e. by the distribution of matter. This in itself is sufficient to exclude the possibility of the exact validity of Euclidean geometry in our universe. But it is conceivable that our universe differs only slightly from a Euclidean one, and this notion seems all the more probable, since calculations show that the metrics of surrounding space is influenced only to an exceedingly small extent by masses even of the magnitude of our sun. We might imagine that, as regards geometry, our universe behaves analogously to a surface which is irregularly curved in its individual parts, but which nowhere departs appreciably from a plane: something like the rippled surface of a lake. Such a universe might fittingly be called a quasi-Euclidean universe. As regards its space it would be infinite. But calculation shows that in a quasi-Euclidean universe the average density of matter would necessarily be nil. Thus such a universe could not be inhabited by matter everywhere ; it would present to us that unsatisfactory picture which we portrayed in Section 30.
If we are to have in the universe an average density of matter which differs from zero, however small may be that difference, then the universe cannot be quasi-Euclidean. On the contrary, the results of calculation indicate that if matter be distributed uniformly, the universe would necessarily be spherical (or elliptical). Since in reality the detailed distribution of matter is not uniform, the real universe will deviate in individual parts from the spherical, i.e. the universe will be quasi-spherical. But it will be necessarily finite. In fact, the theory supplies us with a simple connection 1) between the space-expanse of the universe and the average density of matter in it.
_______________
Notes:
1) For the radius R of the universe we obtain the equation
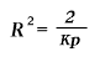
The use of the C.G.S. system in this equation gives 2/k = 1.08.1027; p is the average density of the matter and k is a constant connected with the Newtonian constant of gravitation.
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Appendix I: Simple Derivation of the Lorentz Transformation (Supplementary to Section 11)
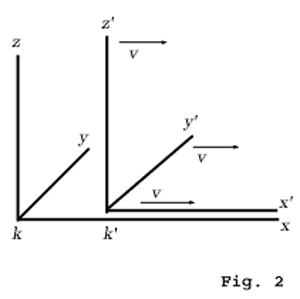
For the relative orientation of the co-ordinate systems indicated in
 ,
,
the x-axes of both systems permanently coincide. In the present case we can divide the problem into parts by considering first only events which are localised on the x-axis. Any such event is represented with respect to the co-ordinate system K by the abscissa x and the time t, and with respect to the system K1 by the abscissa x' and the time t'. We require to find x' and t' when x and t are given.
A light-signal, which is proceeding along the positive axis of x, is transmitted according to the equation
x = ct
or
x - ct = 0 . . . (1).
Since the same light-signal has to be transmitted relative to K1 with the velocity c, the propagation relative to the system K1 will be represented by the analogous formula
x' - ct' = O . . . (2)
Those space-time points (events) which satisfy (x) must also satisfy (2). Obviously this will be the case when the relation
(x' - ct') = λ (x - ct) . . . (3).
is fulfilled in general, where λ indicates a constant ; for, according to (3), the disappearance of (x - ct) involves the disappearance of (x' - ct').
If we apply quite similar considerations to light rays which are being transmitted along the negative x-axis, we obtain the condition
(x' + ct') = µ(x + ct) . . . (4).
By adding (or subtracting) equations (3) and (4), and introducing for convenience the constants a and b in place of the constants λ and µ, where
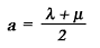
and
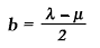
we obtain the equations
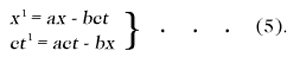
We should thus have the solution of our problem, if the constants a and b were known. These result from the following discussion.
For the origin of K1 we have permanently x' = 0, and hence according to the first of the equations (5)
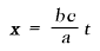
If we call v the velocity with which the origin of K1 is moving relative to K, we then have

The same value v can be obtained from equations (5), if we calculate the velocity of another point of K1 relative to K, or the velocity (directed towards the negative x-axis) of a point of K with respect to K'. In short, we can designate v as the relative velocity of the two systems.
Furthermore, the principle of relativity teaches us that, as judged from K, the length of a unit measuring-rod which is at rest with reference to K1 must be exactly the same as the length, as judged from K', of a unit measuring-rod which is at rest relative to K. In order to see how the points of the x-axis appear as viewed from K, we only require to take a " snapshot " of K1 from K; this means that we have to insert a particular value of t (time of K), e.g. t = 0. For this value of t we then obtain from the first of the equations (5)
x' = ax
Two points of the x'-axis which are separated by the distance Δx' = I when measured in the K1 system are thus separated in our instantaneous photograph by the distance

But if the snapshot be taken from K'(t' = 0), and if we eliminate t from the equations (5), taking into account the expression (6), we obtain
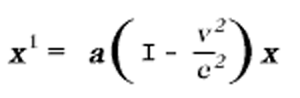
From this we conclude that two points on the x-axis separated by the distance I (relative to K) will be represented on our snapshot by the distance

But from what has been said, the two snapshots must be identical; hence Δx in (7) must be equal to Δx' in (7a), so that we obtain

The equations (6) and (7b) determine the constants a and b. By inserting the values of these constants in (5), we obtain the first and the fourth of the equations given in Section 11.
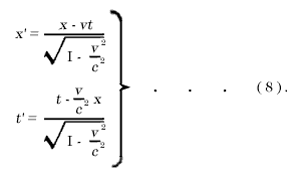
Thus we have obtained the Lorentz transformation for events on the x-axis. It satisfies the condition
x'2 - c2t'2 = x2 - c2t2 . . . (8a).
The extension of this result, to include events which take place outside the x-axis, is obtained by retaining equations (8) and supplementing them by the relations
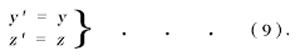
In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K'. This may be shown in the following manner.
We suppose a light-signal sent out from the origin of K at the time t = 0. It will be propagated according to the equation
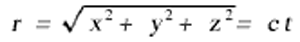
or, if we square this equation, according to the equation
x2 + y2 + z2 = c2t2 = 0 . . . (10).
It is required by the law of propagation of light, in conjunction with the postulate of relativity, that the transmission of the signal in question should take place — as judged from K1 — in accordance with the corresponding formula
r' = ct'
or,
x'2 + y'2 + z'2 - c2t'2 = 0 . . . (10a).
In order that equation (10a) may be a consequence of equation (10), we must have
x'2 + y'2 + z'2 - c2t'2 = σ (x2 + y2 + z2 - c2t2) (11).
Since equation (8a) must hold for points on the x-axis, we thus have σ = I. It is easily seen that the Lorentz transformation really satisfies equation (11) for σ = I; for (11) is a consequence of (8a) and (9), and hence also of (8) and (9). We have thus derived the Lorentz transformation.
The Lorentz transformation represented by (8) and (9) still requires to be generalised. Obviously it is immaterial whether the axes of K1 be chosen so that they are spatially parallel to those of K. It is also not essential that the velocity of translation of K1 with respect to K should be in the direction of the x-axis. A simple consideration shows that we are able to construct the Lorentz transformation in this general sense from two kinds of transformations, viz. from Lorentz transformations in the special sense and from purely spatial transformations. which corresponds to the replacement of the rectangular co-ordinate system by a new system with its axes pointing in other directions.
Mathematically, we can characterise the generalised Lorentz transformation thus :
It expresses x', y', x', t', in terms of linear homogeneous functions of x, y, x, t, of such a kind that the relation
x'2 + y'2 + z'2 - c2t'2 = x2 + y2 + z2 - c2t2 (11a).
is satisfied identically. That is to say: If we substitute their expressions in x, y, x, t, in place of x', y', x', t', on the left-hand side, then the left-hand side of (11a) agrees with the right-hand side.
For the relative orientation of the co-ordinate systems indicated in
 ,
, the x-axes of both systems permanently coincide. In the present case we can divide the problem into parts by considering first only events which are localised on the x-axis. Any such event is represented with respect to the co-ordinate system K by the abscissa x and the time t, and with respect to the system K1 by the abscissa x' and the time t'. We require to find x' and t' when x and t are given.
A light-signal, which is proceeding along the positive axis of x, is transmitted according to the equation
x = ct
or
x - ct = 0 . . . (1).
Since the same light-signal has to be transmitted relative to K1 with the velocity c, the propagation relative to the system K1 will be represented by the analogous formula
x' - ct' = O . . . (2)
Those space-time points (events) which satisfy (x) must also satisfy (2). Obviously this will be the case when the relation
(x' - ct') = λ (x - ct) . . . (3).
is fulfilled in general, where λ indicates a constant ; for, according to (3), the disappearance of (x - ct) involves the disappearance of (x' - ct').
If we apply quite similar considerations to light rays which are being transmitted along the negative x-axis, we obtain the condition
(x' + ct') = µ(x + ct) . . . (4).
By adding (or subtracting) equations (3) and (4), and introducing for convenience the constants a and b in place of the constants λ and µ, where
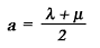
and
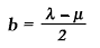
we obtain the equations
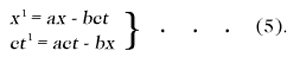
We should thus have the solution of our problem, if the constants a and b were known. These result from the following discussion.
For the origin of K1 we have permanently x' = 0, and hence according to the first of the equations (5)
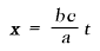
If we call v the velocity with which the origin of K1 is moving relative to K, we then have

The same value v can be obtained from equations (5), if we calculate the velocity of another point of K1 relative to K, or the velocity (directed towards the negative x-axis) of a point of K with respect to K'. In short, we can designate v as the relative velocity of the two systems.
Furthermore, the principle of relativity teaches us that, as judged from K, the length of a unit measuring-rod which is at rest with reference to K1 must be exactly the same as the length, as judged from K', of a unit measuring-rod which is at rest relative to K. In order to see how the points of the x-axis appear as viewed from K, we only require to take a " snapshot " of K1 from K; this means that we have to insert a particular value of t (time of K), e.g. t = 0. For this value of t we then obtain from the first of the equations (5)
x' = ax
Two points of the x'-axis which are separated by the distance Δx' = I when measured in the K1 system are thus separated in our instantaneous photograph by the distance

But if the snapshot be taken from K'(t' = 0), and if we eliminate t from the equations (5), taking into account the expression (6), we obtain
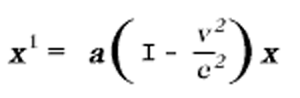
From this we conclude that two points on the x-axis separated by the distance I (relative to K) will be represented on our snapshot by the distance

But from what has been said, the two snapshots must be identical; hence Δx in (7) must be equal to Δx' in (7a), so that we obtain

The equations (6) and (7b) determine the constants a and b. By inserting the values of these constants in (5), we obtain the first and the fourth of the equations given in Section 11.

Thus we have obtained the Lorentz transformation for events on the x-axis. It satisfies the condition
x'2 - c2t'2 = x2 - c2t2 . . . (8a).
The extension of this result, to include events which take place outside the x-axis, is obtained by retaining equations (8) and supplementing them by the relations
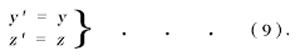
In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K'. This may be shown in the following manner.
We suppose a light-signal sent out from the origin of K at the time t = 0. It will be propagated according to the equation
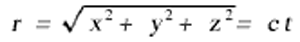
or, if we square this equation, according to the equation
x2 + y2 + z2 = c2t2 = 0 . . . (10).
It is required by the law of propagation of light, in conjunction with the postulate of relativity, that the transmission of the signal in question should take place — as judged from K1 — in accordance with the corresponding formula
r' = ct'
or,
x'2 + y'2 + z'2 - c2t'2 = 0 . . . (10a).
In order that equation (10a) may be a consequence of equation (10), we must have
x'2 + y'2 + z'2 - c2t'2 = σ (x2 + y2 + z2 - c2t2) (11).
Since equation (8a) must hold for points on the x-axis, we thus have σ = I. It is easily seen that the Lorentz transformation really satisfies equation (11) for σ = I; for (11) is a consequence of (8a) and (9), and hence also of (8) and (9). We have thus derived the Lorentz transformation.
The Lorentz transformation represented by (8) and (9) still requires to be generalised. Obviously it is immaterial whether the axes of K1 be chosen so that they are spatially parallel to those of K. It is also not essential that the velocity of translation of K1 with respect to K should be in the direction of the x-axis. A simple consideration shows that we are able to construct the Lorentz transformation in this general sense from two kinds of transformations, viz. from Lorentz transformations in the special sense and from purely spatial transformations. which corresponds to the replacement of the rectangular co-ordinate system by a new system with its axes pointing in other directions.
Mathematically, we can characterise the generalised Lorentz transformation thus :
It expresses x', y', x', t', in terms of linear homogeneous functions of x, y, x, t, of such a kind that the relation
x'2 + y'2 + z'2 - c2t'2 = x2 + y2 + z2 - c2t2 (11a).
is satisfied identically. That is to say: If we substitute their expressions in x, y, x, t, in place of x', y', x', t', on the left-hand side, then the left-hand side of (11a) agrees with the right-hand side.
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Appendix II: Minkowski's Four-Dimensional Space ("World") (supplementary to section 17)
We can characterise the Lorentz transformation still more simply if we introduce the imaginary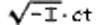 in place of t, as time-variable. If, in accordance with this, we insert
in place of t, as time-variable. If, in accordance with this, we insert
x1 = x
x2 = y
x3 = z
x4 =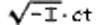
and similarly for the accented system K1, then the condition which is identically satisfied by the transformation can be expressed thus :
x1'2 + x2'2 + x3'2 + x4'2 = x12 + x22 + x32 + x42 (12).
That is, by the afore-mentioned choice of " coordinates," (11a) [see the end of Appendix II] is transformed into this equation.
We see from (12) that the imaginary time co-ordinate x4, enters into the condition of transformation in exactly the same way as the space co-ordinates x1, x2, x3. It is due to this fact that, according to the theory of relativity, the " time "x4, enters into natural laws in the same form as the space co ordinates x1, x2, x3.
A four-dimensional continuum described by the "co-ordinates" x1, x2, x3, x4, was called "world" by Minkowski, who also termed a point-event a " world-point." From a "happening" in three-dimensional space, physics becomes, as it were, an " existence " in the four-dimensional " world."
This four-dimensional " world " bears a close similarity to the three-dimensional " space " of (Euclidean) analytical geometry. If we introduce into the latter a new Cartesian co-ordinate system (x'1, x'2, x'3) with the same origin, then x'1, x'2, x'3, are linear homogeneous functions of x1, x2, x3 which identically satisfy the equation
x'12 + x'22 + x'32 = x12 + x22 + x32
The analogy with (12) is a complete one. We can regard Minkowski's " world " in a formal manner as a four-dimensional Euclidean space (with an imaginary time coordinate) ; the Lorentz transformation corresponds to a " rotation " of the co-ordinate system in the four dimensional " world."
We can characterise the Lorentz transformation still more simply if we introduce the imaginary
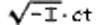 in place of t, as time-variable. If, in accordance with this, we insert
in place of t, as time-variable. If, in accordance with this, we insertx1 = x
x2 = y
x3 = z
x4 =
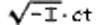
and similarly for the accented system K1, then the condition which is identically satisfied by the transformation can be expressed thus :
x1'2 + x2'2 + x3'2 + x4'2 = x12 + x22 + x32 + x42 (12).
That is, by the afore-mentioned choice of " coordinates," (11a) [see the end of Appendix II] is transformed into this equation.
We see from (12) that the imaginary time co-ordinate x4, enters into the condition of transformation in exactly the same way as the space co-ordinates x1, x2, x3. It is due to this fact that, according to the theory of relativity, the " time "x4, enters into natural laws in the same form as the space co ordinates x1, x2, x3.
A four-dimensional continuum described by the "co-ordinates" x1, x2, x3, x4, was called "world" by Minkowski, who also termed a point-event a " world-point." From a "happening" in three-dimensional space, physics becomes, as it were, an " existence " in the four-dimensional " world."
This four-dimensional " world " bears a close similarity to the three-dimensional " space " of (Euclidean) analytical geometry. If we introduce into the latter a new Cartesian co-ordinate system (x'1, x'2, x'3) with the same origin, then x'1, x'2, x'3, are linear homogeneous functions of x1, x2, x3 which identically satisfy the equation
x'12 + x'22 + x'32 = x12 + x22 + x32
The analogy with (12) is a complete one. We can regard Minkowski's " world " in a formal manner as a four-dimensional Euclidean space (with an imaginary time coordinate) ; the Lorentz transformation corresponds to a " rotation " of the co-ordinate system in the four dimensional " world."
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Appendix III: The Experimental Confirmation of the General Theory of Relativity
From a systematic theoretical point of view, we may imagine the process of evolution of an empirical science to be a continuous process of induction. Theories are evolved and are expressed in short compass as statements of a large number of individual observations in the form of empirical laws, from which the general laws can be ascertained by comparison. Regarded in this way, the development of a science bears some resemblance to the compilation of a classified catalogue. It is, as it were, a purely empirical enterprise.
But this point of view by no means embraces the whole of the actual process ; for it slurs over the important part played by intuition and deductive thought in the development of an exact science. As soon as a science has emerged from its initial stages, theoretical advances are no longer achieved merely by a process of arrangement. Guided by empirical data, the investigator rather develops a system of thought which, in general, is built up logically from a small number of fundamental assumptions, the so-called axioms. We call such a system of thought a theory. The theory finds the justification for its existence in the fact that it correlates a large number of single observations, and it is just here that the " truth " of the theory lies.
Corresponding to the same complex of empirical data, there may be several theories, which differ from one another to a considerable extent. But as regards the deductions from the theories which are capable of being tested, the agreement between the theories may be so complete that it becomes difficult to find any deductions in which the two theories differ from each other. As an example, a case of general interest is available in the province of biology, in the Darwinian theory of the development of species by selection in the struggle for existence, and in the theory of development which is based on the hypothesis of the hereditary transmission of acquired characters.
We have another instance of far-reaching agreement between the deductions from two theories in Newtonian mechanics on the one hand, and the general theory of relativity on the other. This agreement goes so far, that up to the present we have been able to find only a few deductions from the general theory of relativity which are capable of investigation, and to which the physics of pre-relativity days does not also lead, and this despite the profound difference in the fundamental assumptions of the two theories. In what follows, we shall again consider these important deductions, and we shall also discuss the empirical evidence appertaining to them which has hitherto been obtained.
(a) Motion of the Perihelion of Mercury
According to Newtonian mechanics and Newton's law of gravitation, a planet which is revolving round the sun would describe an ellipse round the latter, or, more correctly, round the common centre of gravity of the sun and the planet. In such a system, the sun, or the common centre of gravity, lies in one of the foci of the orbital ellipse in such a manner that, in the course of a planet-year, the distance sun-planet grows from a minimum to a maximum, and then decreases again to a minimum. If instead of Newton's law we insert a somewhat different law of attraction into the calculation, we find that, according to this new law, the motion would still take place in such a manner that the distance sun-planet exhibits periodic variations; but in this case the angle described by the line joining sun and planet during such a period (from perihelion—closest proximity to the sun—to perihelion) would differ from 3600. The line of the orbit would not then be a closed one but in the course of time it would fill up an annular part of the orbital plane, viz. between the circle of least and the circle of greatest distance of the planet from the sun.
According also to the general theory of relativity, which differs of course from the theory of Newton, a small variation from the Newton-Kepler motion of a planet in its orbit should take place, and in such away, that the angle described by the radius sun-planet between one perhelion and the next should exceed that corresponding to one complete revolution by an amount given by
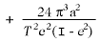
(N.B. — One complete revolution corresponds to the angle 2π in the absolute angular measure customary in physics, and the above expression giver the amount by which the radius sun-planet exceeds this angle during the interval between one perihelion and the next.) In this expression a represents the major semi-axis of the ellipse, e its eccentricity, c the velocity of light, and T the period of revolution of the planet. Our result may also be stated as follows : According to the general theory of relativity, the major axis of the ellipse rotates round the sun in the same sense as the orbital motion of the planet. Theory requires that this rotation should amount to 43 seconds of arc per century for the planet Mercury, but for the other Planets of our solar system its magnitude should be so small that it would necessarily escape detection. 1)
In point of fact, astronomers have found that the theory of Newton does not suffice to calculate the observed motion of Mercury with an exactness corresponding to that of the delicacy of observation attainable at the present time. After taking account of all the disturbing influences exerted on Mercury by the remaining planets, it was found (Leverrier: 1859; and Newcomb: 1895) that an unexplained perihelial movement of the orbit of Mercury remained over, the amount of which does not differ sensibly from the above mentioned +43 seconds of arc per century. The uncertainty of the empirical result amounts to a few seconds only.
(b) Deflection of Light by a Gravitational Field
In Section 22 it has been already mentioned that according to the general theory of relativity, a ray of light will experience a curvature of its path when passing through a gravitational field, this curvature being similar to that experienced by the path of a body which is projected through a gravitational field. As a result of this theory, we should expect that a ray of light which is passing close to a heavenly body would be deviated towards the latter. For a ray of light which passes the sun at a distance of Δ sun-radii from its centre, the angle of deflection (a) should amount to
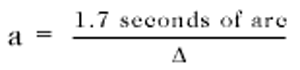
It may be added that, according to the theory, half of
this deflection is produced by the Newtonian field of attraction of the sun, and the other half by the geometrical modification (" curvature ") of space caused by the sun.
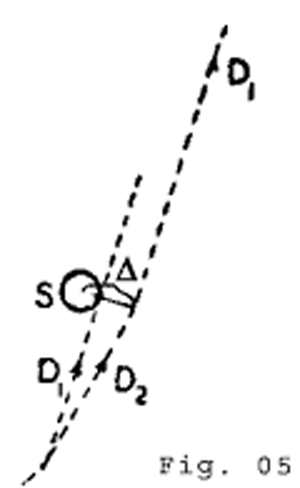
This result admits of an experimental test by means of the photographic registration of stars during a total eclipse of the sun. The only reason why we must wait for a total eclipse is because at every other time the atmosphere is so strongly illuminated by the light from the sun that the stars situated near the sun's disc are invisible. The predicted effect can be seen clearly from the accompanying diagram. If the sun (S) were not present, a star which is practically infinitely distant would be seen in the direction D1, as observed front the earth. But as a consequence of the deflection of light from the star by the sun, the star will be seen in the direction D2, i.e. at a somewhat greater distance from the centre of the sun than corresponds to its real position.
In practice, the question is tested in the following way. The stars in the neighbourhood of the sun are photographed during a solar eclipse. In addition, a second photograph of the same stars is taken when the sun is situated at another position in the sky, i.e. a few months earlier or later. As compared with the standard photograph, the positions of the stars on the eclipse-photograph ought to appear displaced radially outwards (away from the centre of the sun) by an amount corresponding to the angle a.
We are indebted to the [British] Royal Society and to the Royal Astronomical Society for the investigation of this important deduction. Undaunted by the [first world] war and by difficulties of both a material and a psychological nature aroused by the war, these societies equipped two expeditions — to Sobral (Brazil), and to the island of Principe (West Africa) — and sent several of Britain's most celebrated astronomers (Eddington, Cottingham, Crommelin, Davidson), in order to obtain photographs of the solar eclipse of 29th May, 1919. The relative discrepancies to be expected between the stellar photographs obtained during the eclipse and the comparison photographs amounted to a few hundredths of a millimetre only. Thus great accuracy was necessary in making the adjustments required for the taking of the photographs, and in their subsequent measurement.
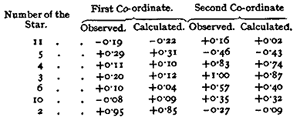
The results of the measurements confirmed the theory in a thoroughly satisfactory manner. The rectangular components of the observed and of the calculated deviations of the stars (in seconds of arc) are set forth in the following table of results :
(c) Displacement of Spectral Lines Towards the Red
In Section 23 it has been shown that in a system K1 which is in rotation with regard to a Galileian system K, clocks of identical construction, and which are considered at rest with respect to the rotating reference-body, go at rates which are dependent on the positions of the clocks. We shall now examine this dependence quantitatively. A clock, which is situated at a distance r from the centre of the disc, has a velocity relative to K which is given by
V = wr
where w represents the angular velocity of rotation of the disc K1 with respect to K. If v0, represents the number of ticks of the clock per unit time (" rate " of the clock) relative to K when the clock is at rest, then the " rate " of the clock (v) when it is moving relative to K with a velocity V, but at rest with respect to the disc, will, in accordance with Section 12, be given by
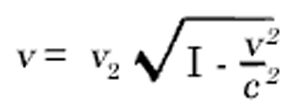
or with sufficient accuracy by
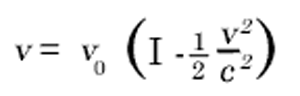
This expression may also be stated in the following form:
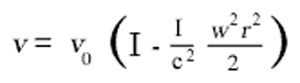
If we represent the difference of potential of the centrifugal force between the position of the clock and the centre of the disc by φ, i.e. the work, considered negatively, which must be performed on the unit of mass against the centrifugal force in order to transport it from the position of the clock on the rotating disc to the centre of the disc, then we have
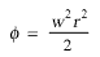
From this it follows that
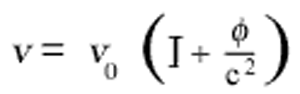
In the first place, we see from this expression that two clocks of identical construction will go at different rates when situated at different distances from the centre of the disc. This result is aiso valid from the standpoint of an observer who is rotating with the disc.
Now, as judged from the disc, the latter is in a gravitational field of potential φ, hence the result we have obtained will hold quite generally for gravitational fields. Furthermore, we can regard an atom which is emitting spectral lines as a clock, so that the following statement will hold:
An atom absorbs or emits light of a frequency which is dependent on the potential of the gravitational field in which it is situated.
The frequency of an atom situated on the surface of a heavenly body will be somewhat less than the frequency of an atom of the same element which is situated in free space (or on the surface of a smaller celestial body).
Now φ = - K (M/r), where K is Newton's constant of gravitation, and M is the mass of the heavenly body. Thus a displacement towards the red ought to take place for spectral lines produced at the surface of stars as compared with the spectral lines of the same element produced at the surface of the earth, the amount of this displacement being
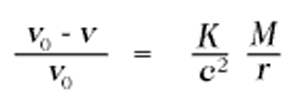
For the sun, the displacement towards the red predicted by theory amounts to about two millionths of the wave-length. A trustworthy calculation is not possible in the case of the stars, because in general neither the mass M nor the radius r are known.
It is an open question whether or not this effect exists, and at the present time (1920) astronomers are working with great zeal towards the solution. Owing to the smallness of the effect in the case of the sun, it is difficult to form an opinion as to its existence. Whereas Grebe and Bachem (Bonn), as a result of their own measurements and those of Evershed and Schwarzschild on the cyanogen bands, have placed the existence of the effect almost beyond doubt, while other investigators, particularly St. John, have been led to the opposite opinion in consequence of their measurements.
Mean displacements of lines towards the less refrangible end of the spectrum are certainly revealed by statistical investigations of the fixed stars ; but up to the present the examination of the available data does not allow of any definite decision being arrived at, as to whether or not these displacements are to be referred in reality to the effect of gravitation. The results of observation have been collected together, and discussed in detail from the standpoint of the question which has been engaging our attention here, in a paper by E. Freundlich entitled "Zur Prüfung der allgemeinen Relativitäts-Theorie" (Die Naturwissenschaften, 1919, No. 35, p. 520: Julius Springer, Berlin).
At all events, a definite decision will be reached during the next few years. If the displacement of spectral lines towards the red by the gravitational potential does not exist, then the general theory of relativity will be untenable. On the other hand, if the cause of the displacement of spectral lines be definitely traced to the gravitational potential, then the study of this displacement will furnish us with important information as to the mass of the heavenly bodies. [A]
_______________
Notes:
1) Especially since the next planet Venus has an orbit that is almost an exact circle, which makes it more difficult to locate the perihelion with precision.
[A] The displacement of spectral lines towards the red end of the spectrum was definitely established by Adams in 1924, by observations on the dense companion of Sirius, for which the effect is about thirty times greater than for the Sun. R.W.L. — translator
From a systematic theoretical point of view, we may imagine the process of evolution of an empirical science to be a continuous process of induction. Theories are evolved and are expressed in short compass as statements of a large number of individual observations in the form of empirical laws, from which the general laws can be ascertained by comparison. Regarded in this way, the development of a science bears some resemblance to the compilation of a classified catalogue. It is, as it were, a purely empirical enterprise.
But this point of view by no means embraces the whole of the actual process ; for it slurs over the important part played by intuition and deductive thought in the development of an exact science. As soon as a science has emerged from its initial stages, theoretical advances are no longer achieved merely by a process of arrangement. Guided by empirical data, the investigator rather develops a system of thought which, in general, is built up logically from a small number of fundamental assumptions, the so-called axioms. We call such a system of thought a theory. The theory finds the justification for its existence in the fact that it correlates a large number of single observations, and it is just here that the " truth " of the theory lies.
Corresponding to the same complex of empirical data, there may be several theories, which differ from one another to a considerable extent. But as regards the deductions from the theories which are capable of being tested, the agreement between the theories may be so complete that it becomes difficult to find any deductions in which the two theories differ from each other. As an example, a case of general interest is available in the province of biology, in the Darwinian theory of the development of species by selection in the struggle for existence, and in the theory of development which is based on the hypothesis of the hereditary transmission of acquired characters.
We have another instance of far-reaching agreement between the deductions from two theories in Newtonian mechanics on the one hand, and the general theory of relativity on the other. This agreement goes so far, that up to the present we have been able to find only a few deductions from the general theory of relativity which are capable of investigation, and to which the physics of pre-relativity days does not also lead, and this despite the profound difference in the fundamental assumptions of the two theories. In what follows, we shall again consider these important deductions, and we shall also discuss the empirical evidence appertaining to them which has hitherto been obtained.
(a) Motion of the Perihelion of Mercury
According to Newtonian mechanics and Newton's law of gravitation, a planet which is revolving round the sun would describe an ellipse round the latter, or, more correctly, round the common centre of gravity of the sun and the planet. In such a system, the sun, or the common centre of gravity, lies in one of the foci of the orbital ellipse in such a manner that, in the course of a planet-year, the distance sun-planet grows from a minimum to a maximum, and then decreases again to a minimum. If instead of Newton's law we insert a somewhat different law of attraction into the calculation, we find that, according to this new law, the motion would still take place in such a manner that the distance sun-planet exhibits periodic variations; but in this case the angle described by the line joining sun and planet during such a period (from perihelion—closest proximity to the sun—to perihelion) would differ from 3600. The line of the orbit would not then be a closed one but in the course of time it would fill up an annular part of the orbital plane, viz. between the circle of least and the circle of greatest distance of the planet from the sun.
According also to the general theory of relativity, which differs of course from the theory of Newton, a small variation from the Newton-Kepler motion of a planet in its orbit should take place, and in such away, that the angle described by the radius sun-planet between one perhelion and the next should exceed that corresponding to one complete revolution by an amount given by
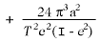
(N.B. — One complete revolution corresponds to the angle 2π in the absolute angular measure customary in physics, and the above expression giver the amount by which the radius sun-planet exceeds this angle during the interval between one perihelion and the next.) In this expression a represents the major semi-axis of the ellipse, e its eccentricity, c the velocity of light, and T the period of revolution of the planet. Our result may also be stated as follows : According to the general theory of relativity, the major axis of the ellipse rotates round the sun in the same sense as the orbital motion of the planet. Theory requires that this rotation should amount to 43 seconds of arc per century for the planet Mercury, but for the other Planets of our solar system its magnitude should be so small that it would necessarily escape detection. 1)
In point of fact, astronomers have found that the theory of Newton does not suffice to calculate the observed motion of Mercury with an exactness corresponding to that of the delicacy of observation attainable at the present time. After taking account of all the disturbing influences exerted on Mercury by the remaining planets, it was found (Leverrier: 1859; and Newcomb: 1895) that an unexplained perihelial movement of the orbit of Mercury remained over, the amount of which does not differ sensibly from the above mentioned +43 seconds of arc per century. The uncertainty of the empirical result amounts to a few seconds only.
(b) Deflection of Light by a Gravitational Field
In Section 22 it has been already mentioned that according to the general theory of relativity, a ray of light will experience a curvature of its path when passing through a gravitational field, this curvature being similar to that experienced by the path of a body which is projected through a gravitational field. As a result of this theory, we should expect that a ray of light which is passing close to a heavenly body would be deviated towards the latter. For a ray of light which passes the sun at a distance of Δ sun-radii from its centre, the angle of deflection (a) should amount to
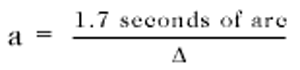
It may be added that, according to the theory, half of

this deflection is produced by the Newtonian field of attraction of the sun, and the other half by the geometrical modification (" curvature ") of space caused by the sun.
This result admits of an experimental test by means of the photographic registration of stars during a total eclipse of the sun. The only reason why we must wait for a total eclipse is because at every other time the atmosphere is so strongly illuminated by the light from the sun that the stars situated near the sun's disc are invisible. The predicted effect can be seen clearly from the accompanying diagram. If the sun (S) were not present, a star which is practically infinitely distant would be seen in the direction D1, as observed front the earth. But as a consequence of the deflection of light from the star by the sun, the star will be seen in the direction D2, i.e. at a somewhat greater distance from the centre of the sun than corresponds to its real position.
In practice, the question is tested in the following way. The stars in the neighbourhood of the sun are photographed during a solar eclipse. In addition, a second photograph of the same stars is taken when the sun is situated at another position in the sky, i.e. a few months earlier or later. As compared with the standard photograph, the positions of the stars on the eclipse-photograph ought to appear displaced radially outwards (away from the centre of the sun) by an amount corresponding to the angle a.
We are indebted to the [British] Royal Society and to the Royal Astronomical Society for the investigation of this important deduction. Undaunted by the [first world] war and by difficulties of both a material and a psychological nature aroused by the war, these societies equipped two expeditions — to Sobral (Brazil), and to the island of Principe (West Africa) — and sent several of Britain's most celebrated astronomers (Eddington, Cottingham, Crommelin, Davidson), in order to obtain photographs of the solar eclipse of 29th May, 1919. The relative discrepancies to be expected between the stellar photographs obtained during the eclipse and the comparison photographs amounted to a few hundredths of a millimetre only. Thus great accuracy was necessary in making the adjustments required for the taking of the photographs, and in their subsequent measurement.
The results of the measurements confirmed the theory in a thoroughly satisfactory manner. The rectangular components of the observed and of the calculated deviations of the stars (in seconds of arc) are set forth in the following table of results :

(c) Displacement of Spectral Lines Towards the Red
In Section 23 it has been shown that in a system K1 which is in rotation with regard to a Galileian system K, clocks of identical construction, and which are considered at rest with respect to the rotating reference-body, go at rates which are dependent on the positions of the clocks. We shall now examine this dependence quantitatively. A clock, which is situated at a distance r from the centre of the disc, has a velocity relative to K which is given by
V = wr
where w represents the angular velocity of rotation of the disc K1 with respect to K. If v0, represents the number of ticks of the clock per unit time (" rate " of the clock) relative to K when the clock is at rest, then the " rate " of the clock (v) when it is moving relative to K with a velocity V, but at rest with respect to the disc, will, in accordance with Section 12, be given by
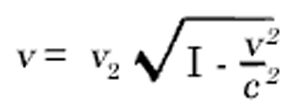
or with sufficient accuracy by
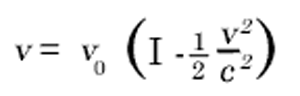
This expression may also be stated in the following form:
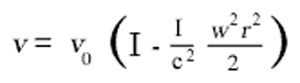
If we represent the difference of potential of the centrifugal force between the position of the clock and the centre of the disc by φ, i.e. the work, considered negatively, which must be performed on the unit of mass against the centrifugal force in order to transport it from the position of the clock on the rotating disc to the centre of the disc, then we have
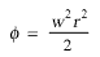
From this it follows that
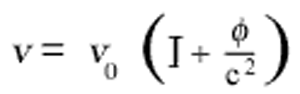
In the first place, we see from this expression that two clocks of identical construction will go at different rates when situated at different distances from the centre of the disc. This result is aiso valid from the standpoint of an observer who is rotating with the disc.
Now, as judged from the disc, the latter is in a gravitational field of potential φ, hence the result we have obtained will hold quite generally for gravitational fields. Furthermore, we can regard an atom which is emitting spectral lines as a clock, so that the following statement will hold:
An atom absorbs or emits light of a frequency which is dependent on the potential of the gravitational field in which it is situated.
The frequency of an atom situated on the surface of a heavenly body will be somewhat less than the frequency of an atom of the same element which is situated in free space (or on the surface of a smaller celestial body).
Now φ = - K (M/r), where K is Newton's constant of gravitation, and M is the mass of the heavenly body. Thus a displacement towards the red ought to take place for spectral lines produced at the surface of stars as compared with the spectral lines of the same element produced at the surface of the earth, the amount of this displacement being
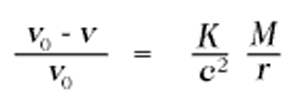
For the sun, the displacement towards the red predicted by theory amounts to about two millionths of the wave-length. A trustworthy calculation is not possible in the case of the stars, because in general neither the mass M nor the radius r are known.
It is an open question whether or not this effect exists, and at the present time (1920) astronomers are working with great zeal towards the solution. Owing to the smallness of the effect in the case of the sun, it is difficult to form an opinion as to its existence. Whereas Grebe and Bachem (Bonn), as a result of their own measurements and those of Evershed and Schwarzschild on the cyanogen bands, have placed the existence of the effect almost beyond doubt, while other investigators, particularly St. John, have been led to the opposite opinion in consequence of their measurements.
Mean displacements of lines towards the less refrangible end of the spectrum are certainly revealed by statistical investigations of the fixed stars ; but up to the present the examination of the available data does not allow of any definite decision being arrived at, as to whether or not these displacements are to be referred in reality to the effect of gravitation. The results of observation have been collected together, and discussed in detail from the standpoint of the question which has been engaging our attention here, in a paper by E. Freundlich entitled "Zur Prüfung der allgemeinen Relativitäts-Theorie" (Die Naturwissenschaften, 1919, No. 35, p. 520: Julius Springer, Berlin).
At all events, a definite decision will be reached during the next few years. If the displacement of spectral lines towards the red by the gravitational potential does not exist, then the general theory of relativity will be untenable. On the other hand, if the cause of the displacement of spectral lines be definitely traced to the gravitational potential, then the study of this displacement will furnish us with important information as to the mass of the heavenly bodies. [A]
_______________
Notes:
1) Especially since the next planet Venus has an orbit that is almost an exact circle, which makes it more difficult to locate the perihelion with precision.
[A] The displacement of spectral lines towards the red end of the spectrum was definitely established by Adams in 1924, by observations on the dense companion of Sirius, for which the effect is about thirty times greater than for the Sun. R.W.L. — translator
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
Re: Relativity, The Special and General Theory
Appendix IV: The Structure of Space According to the General Theory of Relativity (Supplementary to Section 32)
Since the publication of the first edition of this little book, our knowledge about the structure of space in the large (" cosmological problem ") has had an important development, which ought to be mentioned even in a popular presentation of the subject.
My original considerations on the subject were based on two hypotheses:
(1) There exists an average density of matter in the whole of space which is everywhere the same and different from zero.
(2) The magnitude (" radius ") of space is independent of time.
Both these hypotheses proved to be consistent, according to the general theory of relativity, but only after a hypothetical term was added to the field equations, a term which was not required by the theory as such nor did it seem natural from a theoretical point of view (" cosmological term of the field equations ").
Hypothesis (2) appeared unavoidable to me at the time, since I thought that one would get into bottomless speculations if one departed from it.
However, already in the 'twenties, the Russian mathematician Friedman showed that a different hypothesis was natural from a purely theoretical point of view. He realized that it was possible to preserve hypothesis (1) without introducing the less natural cosmological term into the field equations of gravitation, if one was ready to drop hypothesis (2). Namely, the original field equations admit a solution in which the " world radius " depends on time (expanding space). In that sense one can say, according to Friedman, that the theory demands an expansion of space.
A few years later Hubble showed, by a special investigation of the extra-galactic nebulae (" milky ways "), that the spectral lines emitted showed a red shift which increased regularly with the distance of the nebulae. This can be interpreted in regard to our present knowledge only in the sense of Doppler's principle, as an expansive motion of the system of stars in the large — as required, according to Friedman, by the field equations of gravitation. Hubble's discovery can, therefore, be considered to some extent as a confirmation of the theory.
There does arise, however, a strange difficulty. The interpretation of the galactic line-shift discovered by Hubble as an expansion (which can hardly be doubted from a theoretical point of view), leads to an origin of this expansion which lies " only " about 109 years ago, while physical astronomy makes it appear likely that the development of individual stars and systems of stars takes considerably longer. It is in no way known how this incongruity is to be overcome.
I further want to remark that the theory of expanding space, together with the empirical data of astronomy, permit no decision to be reached about the finite or infinite character of (three-dimensional) space, while the original " static " hypothesis of space yielded the closure (finiteness) of space.
Since the publication of the first edition of this little book, our knowledge about the structure of space in the large (" cosmological problem ") has had an important development, which ought to be mentioned even in a popular presentation of the subject.
My original considerations on the subject were based on two hypotheses:
(1) There exists an average density of matter in the whole of space which is everywhere the same and different from zero.
(2) The magnitude (" radius ") of space is independent of time.
Both these hypotheses proved to be consistent, according to the general theory of relativity, but only after a hypothetical term was added to the field equations, a term which was not required by the theory as such nor did it seem natural from a theoretical point of view (" cosmological term of the field equations ").
Hypothesis (2) appeared unavoidable to me at the time, since I thought that one would get into bottomless speculations if one departed from it.
However, already in the 'twenties, the Russian mathematician Friedman showed that a different hypothesis was natural from a purely theoretical point of view. He realized that it was possible to preserve hypothesis (1) without introducing the less natural cosmological term into the field equations of gravitation, if one was ready to drop hypothesis (2). Namely, the original field equations admit a solution in which the " world radius " depends on time (expanding space). In that sense one can say, according to Friedman, that the theory demands an expansion of space.
A few years later Hubble showed, by a special investigation of the extra-galactic nebulae (" milky ways "), that the spectral lines emitted showed a red shift which increased regularly with the distance of the nebulae. This can be interpreted in regard to our present knowledge only in the sense of Doppler's principle, as an expansive motion of the system of stars in the large — as required, according to Friedman, by the field equations of gravitation. Hubble's discovery can, therefore, be considered to some extent as a confirmation of the theory.
There does arise, however, a strange difficulty. The interpretation of the galactic line-shift discovered by Hubble as an expansion (which can hardly be doubted from a theoretical point of view), leads to an origin of this expansion which lies " only " about 109 years ago, while physical astronomy makes it appear likely that the development of individual stars and systems of stars takes considerably longer. It is in no way known how this incongruity is to be overcome.
I further want to remark that the theory of expanding space, together with the empirical data of astronomy, permit no decision to be reached about the finite or infinite character of (three-dimensional) space, while the original " static " hypothesis of space yielded the closure (finiteness) of space.
- admin
- Site Admin
- Posts: 37583
- Joined: Thu Aug 01, 2013 5:21 am
38 posts
• Page 4 of 4 • 1, 2, 3, 4
Who is online
Users browsing this forum: No registered users and 1 guest
