Dated Texts of the Old Kingdom [Old Kingdom Annals] [The Palermo Stone]
by von Anthony Spalinger
Studien zur Altägyptischen Kultur , Bd. 21 (1994), pp. 275-319
1994
The king-list that Manetho had access to is unknown to us, but of the surviving king-lists, the one most similar to his is the Turin Royal Canon (or Turin Papyrus). The oldest source with which we can compare to Manetho are the Old Kingdom Annals (c. 2500-2200 BC). From the New Kingdom are the list at Karnak (constructed by order of Thutmose III), two at Abydos (by Seti I and Ramesses II— the latter a duplicate, but updated version of the former), and the Saqqara list by the priest Tenry.
The provenance of the Old Kingdom Annals is unknown, surviving as the Palermo Stone. The differences between the Annals and Manetho are great. The Annals only reach to the fifth dynasty, but its pre-dynastic rulers are listed as the kings of Lower Egypt and kings of Upper Egypt. By contrast, Manetho lists several Greek and Egyptian deities beginning with Hephaistos and Helios. Secondly, the Annals give annual reports of the activities of the kings, while there is little probability that Manetho would have been able to go into such detail.
The New Kingdom lists are each selective in their listings: that of Seti I, for instance, lists seventy-six kings from dynasties one to nineteen, omitting the Hyksos rulers and those associated with the heretic Akhenaten. The Saqqara king list, contemporaneous with Ramesses II, has fifty-eight names, with similar omissions. If Manetho used these lists at all, he would have been unable to get all of his information from them alone, due to the selective nature of their records. Verbrugghe and Wickersham argue:[...] The purpose of these lists was to cover the walls of a sacred room in which the reigning Pharaoh (or other worshiper, as in the case of Tenry and his Saqqara list) made offerings or prayers to his or her predecessors, imagined as ancestors. Each royal house had a particular traditional list of these "ancestors," different from that of the other houses. The purpose of these lists is not historical but religious. It is not that they are trying and failing to give a complete list. They are not trying at all. Seti and Ramesses did not wish to make offerings to Akhenaten, Tutankhamen, or Hatshepsut, and that is why they are omitted, not because their existence was unknown or deliberately ignored in a broader historical sense. For this reason, the Pharaonic king-lists were generally wrong for Manetho's purposes, and we should commend Manetho for not basing his account on them (2000:105).
-- Manetho [Manethon], by Wikipedia
To the memory of Richard Anthony Parker
As a background to the chronology of the earlier phases of Egyptian civilization, [it is] necessary to draw up all the available evidence pertaining to the regnal years kings. This task, although arduous, is of great benefit, for with such a list [we are] able to see, more precisely, the skeleton upon which we moderns locate our reconstructions. The following analysis purports to be as complete as possible; the author all too well realizes that many more dated texts are awaiting publication. [He] is certain, however, that with this data in hand, one can easily survey the regnal year dating from Dynasty 4 to 6 in a clearer and more complete fashion [than] previously. In other words, the purpose of this study is overtly pragmatic. Weavings of modern pseudo-Manethonian speculations have [not?] been permitted [in] this article. Quite to the contrary, the writer has as his aim a more modest scientific approach: namely, the desire to reconstitute the development of Egyptian [history] keeping from the basal phase of Dynastic civilization (presently inappropriately Dynasty "0") to the end of the Memphite monarchy at the close of the 8th. Questions of a mundane nature concerned with text attribution will be covered as, at least for some, the more crucial problem is whether a biennial system operated, and if so, can we determine exactly when it ended.
I have little energy and patience with the plethora of studies concerning reconstruction [of] the Palermo Stone.
The Palermo Stone, the fragment of the Egyptian Royal Annals housed in Palermo, Italy.
A fragment of the Royal Annals, on display at the Petrie Museum, London, which is inscribed with part of the Khasekhemwy register and at the bottom with a sign from the Sneferu register
The Palermo Stone is one of seven surviving fragments of a stele known as the Royal Annals of the Old Kingdom of Ancient Egypt. The stele contained a list of the kings of Egypt from the First Dynasty (c. 3150–2890 BCE) through to the early part of the Fifth Dynasty (c. 2392–2283 BCE) and noted significant events in each year of their reigns. It was probably made during the Fifth Dynasty. The Palermo Stone is held in the Regional Archeological Museum Antonio Salinas in the city of Palermo, Italy, from which it derives its name.
The term "Palermo Stone" is sometimes applied to all seven surviving fragments of the Royal Annals, including those held in museums in Cairo and London. The fragments are also sometimes described collectively as the "Cairo Annals Stone", although the term "Cairo Stone" is also used to mean only those fragments of the Royal Annals now in Cairo.
The Palermo Stone and other fragments of the Royal Annals preserve what is probably the oldest historical text that has survived from Ancient Egypt and form a key source for Egyptian history in the Old Kingdom....
The inscription on the "front" (recto) of the Palermo Stone consists of six horizontal bands or registers of hieroglyphic text running right to left. The first register lists the names of predynastic kings of Lower Egypt (identified as such by the wearing of the Red Crown). The second and subsequent registers contain portions of royal annals for pharaohs of the First to Fourth Dynasties, that is lists of the key events in each year of the reign of each king, arranged chronologically. The second register on the Palermo Stone begins with the final year entries for a king of the First Dynasty whose name is not preserved, but who is generally assumed to be either Narmer or Aha. The rest of the second register is taken up with the first nine annual entries for this king's successor, who is again not named on the fragment, but is assumed to be either Aha or his successor Djer. The remainder of the inscription on this side continues with royal annals down to the kings of the Fourth Dynasty.
The text continues on the "back" (verso) of the Palermo Stone, cataloguing events during the reigns of pharaohs down to Neferirkare Kakai, third ruler of the Fifth Dynasty. From the surviving fragments it is unclear whether the Royal Annals originally continued beyond this point in time. Where a king is named, the name of his mother is also recorded, such as Betrest mother of the First Dynasty king Semerkhet and Meresankh I mother of the Fourth Dynasty king Seneferu.
Information recorded in the Royal Annals (as preserved on the Palermo Stone) includes measurements of the height of the annual Nile flood (see Nilometer), the inundation, details of festivals (such as Sed festivals), taxation, sculpture, buildings, and warfare.
The original location of the stele is unknown and none of the surviving fragments have a secure archeological provenance. One fragment now in Cairo is said to have been found at an archaeological site at Memphis, while three other fragments now in Cairo were said to have been found in Middle Egypt. No find site for the Palermo Stone itself has been suggested.
The Palermo Stone was purchased by a Sicilian lawyer, Ferdinand Guidano, in 1859 and it has been in Palermo since 1866. On 19 October 1877, it was presented to the Palermo Archaeological Museum by the Guidano family, where it has remained since.
There are five fragments of the Royal Annals in the Egyptian Museum in Cairo, four of which were acquired between 1895 and 1914. The fifth was purchased on the antiquities market in 1963. One small fragment is in the Petrie Museum of University College London, forming part of the collection of the archeologist Sir Flinders Petrie (and purchased by him in 1914)....
There are uncertainties regarding the date of the Palermo Stone and of the Royal Annals it records. It is unknown whether the inscription was done in one go or was added to over time. It is also unknown whether it dates from the period it describes (i.e. from no later than the Fifth Dynasty). It has been suggested that the stele was made much later, perhaps in the Twenty-fifth Dynasty (747–656 BCE)....
It is also unknown whether all the surviving fragments are part of the same stele or come from different copies. It is possible that at least one of the smaller fragments held in Cairo (none of which have any clear provenance) is not genuine.
The text is difficult to decipher due both to the state of preservation of the inscription (which varies widely) and due to its antiquity. If the text is a later copy, rather than a Fifth Dynasty original, there is also the possibility that errors and invention crept in during the copying process....
New Kingdom Egyptian king lists, such as the Turin Canon (13th century BCE) and the Abydos king list (reign of Seti I, 1294–1279 BCE), identify Menes (probably Narmer) (c. 3100 or 3000 BCE) as the first king of the First Dynasty and so credit him with unifying Egypt. However, the top register of the Royal Annals names some predynastic rulers of Upper and Lower Egypt, presumably referring to a time before Egypt was unified. Identification of these kings with historical persons remains controversial.
The ancient historian Manetho may have used information similar to the complete Royal Annals stele to construct his chronology of the early dynasties of Egypt, forming part of his Aegyptiaca ...
-- Palermo Stone, by Wikipedia
Until a first-rate publication by Egyptologist is provided, hopefully with direct input from a chronologist, it [is un]necessary to spend my late hours creating phantasms based on the measurement [of the] unseen Palermo Stone. Far more worthwhile, it seems, is the effort to blaze [a] trail through the gourse and bracken of the contemporary dated inscriptions, though some of them may be, in order to achieve some well-marked path travelers [can] use. It is with more than a tinge of great admiration and respect [for the] chronological giant R.A. Parker, who made the effort to precede his intricate mathematical calculations with accurate historical analyses, that this study is dedicated.
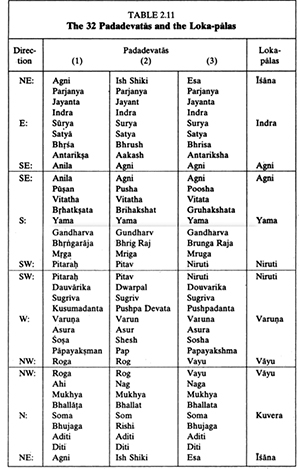
Before turning to our list of dated inscriptions, a few words concern[ing] the limitations of one of our earlier sources, the so-called Old Kingdom Annals (Palermo Stone), are necessary. Many have noted the difficulties in historical reckoning evident on that monument. Supporting the position that there are many irregularities in dating throughout the period covered by the Palermo Stone are the following indications1. First, as previously noted, and often commented on, Snefru has two counts next to one another. The situation is compounded when the obvious omissions are stressed: there is no "year after the 7th count," and the year preceding "count 7" has no indication at all. That is to say, at least in the reign of Snefru, the following occurred: (1) at least one year was devoid of any explicit dating reference; (2) there was no year denoted as "year after the occurrence of the 7th count"; and (3) "count 8" follows on "count 7". Of equal importance is the lack of any parallel guide such as the regular biennial [taking place every other year] Sms Hr references that seem to have been part and parcel of the Archaic Age, as well as Dynasty 32. The last three indications of this occurrence are to be found for Horuses Nebka and Djoser in line 5 of the Annals. (I do not feel that Kaiser was correct to place the London fragment into the reign of Huni3.)
More useful are the recently published inscribed vases from Elephantine4.
Dating the corpus
While some jars come from securely dated contexts, others have been found in temple repositories at Elephantine, Hierakonpolis, Abydos and Tell Ibrahim Awad. These repositories appear to be mixed deposits of earlier and later temple equipment and votive material. However, as both the Main Deposit and the Osiris/Khenti-amentiu Temple excavations were conducted many years ago, the records must be treated with some caution. For example, Petrie gave level numbers to objects found in the Osiris/Khenti-amentiu Temple,31 [1 Abydos II, 3 ] but as Kemp convincingly demonstrates, the relationship between the level numbers, the overall stratigraphy and Petrie's dating of the site is precarious. 32 [32 See his discussion in MDAIK 23, 138-9, 148.]
The temple repositories at Elephantine and Tell Ibrahim Awad have been excavated more recently, allowing a reliable assessment of the stratigraphy. Nevertheless the repositories at these two sites share a common problem with Abydos and Hierakonpolis: all are 'open' deposits of temple equipment with a potentially wide date range when appraised on stratigraphic grounds. For example, in his examination of Chamber M69 in the Abydos Temple, Kemp allows that 'some of the objects, by their style, do seem to belong to the first two dynasties'.33 [Ibid. 154.] Petrie himself considered M69 as temple 'garbage' deposited around the middle of the Second Dynasty.34 [Abydos II, 23.] However, according to Kemp, the top of M69 is at the level of the Old Kingdom temple floor, resulting in a date of deposition for the objects as late as the Sixth Dynasty or even the early Eighteenth Dynasty, based on other evidence.35 [MDAIK 23, 153-5.] All that can be said with certainty is that while some material is undoubtedly early, later material is also probably included, making parallels drawn from M69 and similar open deposits less secure for dating purposes. As the problem posed by the repositories has been widely discussed by other scholars, further debate on the issue here is unnecessary.36 [In addition to Kemp, see Dreyer, Elephantine VIII, 44-52; S. Harvey, 'A Decorated Protodynastic Cult Stand from Abydos', in P. Der Manuelian (ed.), Studies in Honor of William Kelly Simpson (Boston, 1996), I, 367-8.] As Kemp suggests, the only valid method for dating uninscribed objects from such contexts is stylistic parallel. Nevertheless, if most of the available parallels come from similar strata, a circular dating argument arises that cannot be tested against more clearly stratified material.
In the case of hes-jars as a group, further study would identify more precise typological changes. For most of the jars in the catalogue, parallels exist from beyond the temple repositories, either for the whole vessel, or for elements of the shape. Many of the wide-mouthed vessels (Types 1, 2, 4 and 5) either come from reliable Early Dynastic contexts or have parallels securing this date. A Third Dynasty date is also possible for 2. At Elephantine and Tell Ibrahim Awad, temple deposits with black-topped pots date to the Old Kingdom (6, 7, 12), but typologically the vessels have closest links with those from the Early Dynastic Period. Paradoxically, they are in excellent condition. However, the narrow-necked jars from Abydos (15 and 16) may have a longer date range. Good parallels for this type come from the Old Kingdom, with only one similar Early dynastic form known from Naqada.37 [Petrie, Abydos II, 29, pl. xliii.] This vessel was found many years ago in an excavation that cannot be regarded as reliable by modern standards.
-- Black-Topped Ware in Early Dynastic Contexts, by Karin N. Sowada, The Journal of Egyptian Archaeology, 1999, Vol. 85 (1999), pp. 85-102.
Dated to the late 3rd Dynasty, they reveal a system virtually identical to the evidence from the Old Kingdom Annals. For example, one of the jar inscriptions commences on the right with an oversized rnpt sign. (This is to be expected: see our comments below.) This jar (No. 1 of the publication has two separate texts: (1) year of the Sms Hr, then follows the specific description of the events of that year; and (2) "Year of the Sms Hr, 11th occasion of..." Dreyer attempted to link the reference to the "11th occasion" (zp 11) with the following description of a local event rather than with any specific regnal year indication. This is reasonable insofar as the Annals do not number the various (biennial) Sms Hr occasions. The king under whom this inscription was inscribed is unknown; Dreyer mentioned Huni only because the Turin Canon has given him 24 years. Other possibilities may be proposed from Manetho's garbled account of Dynasty 3: Aches, for example (42 years), as well as Sephuris (30 years) and Kerp(heres) (26 years). The third vase inscription presents a further common opening section: "Year of the appearance of the King of Upper and Lower Egypt"; it does not belong to one of the regular Sms Hr years.
The importance of this recent find cannot be underestimated. These two vases present contemporary and early evidence of the regnal year dating from Egypt. Owing to the lack of any associated "count" (tnwt) with Sms Hr notations, it can be possible to limit the timeframe: namely, at least one of the two vases should not be placed to Nebka's reign. The reason for this is simple: the Annals indicate a count associated with the (still) biennial procession of the king. Hence, Dreyer's possibility of Huni seems best. The similar evidence from the Step Pyramid excavations presents a useful parallel which will be discussed in more detail below. However, it is sufficient to observe the presence of the Sms Hr event there as well; the counting, however, seems more regularized than on the vases from Elephantine.
A useful point of approach concerns these biennial Sms Hr events themselves5. For the commencement of Djer's reign Sms Hr definitely began with the second regnal year, probably as the first was short of the expected 365 days in the civil year and, more importantly, the event was of national occurrence and a must to perform after the opening commencement year had passed. Hence, we see the same practice of Djer adhered to by Semerkhet. But with Djoser such was not the case even though his reign is often claimed to be the one that oversaw the transformation to a standardization of administration, society, and kingship.
Further disconcerting in this context is the absence of any associated count with Djoser. The Palermo Stone is clear on this point: with Nebka the Sms Hr are linked with the counts and both apparently occurred in the even years (as a norm). Between any two there was no title or definition such as "year after the Xth count". That practice, at least on the Annals, would come later. But it is surprising to see that Nebka's penultimate regnal year saw the Sms Hr in conjunction with the "8th count".
The exact location of these counts plays an important role in the interpretation by Redford of the development of the Old Kingdom Annals6. He observed that the Egyptian zp X followed by tnwt was always placed at the end of the regnal year box. That is to say, the opening rnpt was not overtly or indirectly connected either with the idea of a count (zp). Quite the contrary, the ubiquitous term Sms Hr was the one that immediately followed the rnpt sign. This being so, it is easy to see why the standard regnal year system of later ages did not owe its origins first to the counts and why such a system was not at all regular. Indeed, one has but to mention the two cases of a count of gold plus field(s) to see that the later standard of a cattle census was not yet firm as cement. Finally, with Userkaf the Palermo Stone as well as its Cairo counterpart (Fragment No. 1) reveal the presence of the cattle census. In this king's reign the first addition of a cattle determinative will be found in two separate years. Moreover, the addition of "year after the Xth occasion of the count of cattle" is recorded on the Cairo fragment. For Sahure, the situation is not so easy to unravel.
A useful indication of the development of regnal years may, in fact, be derived from some simple rules of Egyptian grammar. It was Edel who pointed out in a definitive fashion that the word zp, "time", "occasion" must be connected with an ordinal number immediately following7. The word tpy (and not just a single stroke) proves this. Moreover, since the word for "first", "second", and so forth is not feminine, the phrase rnpt zp tpy must indicate that a literal translation of "year of the first occasion" and not "first year of the occasion" was meant. This implies that, as might be expected, the original of the regnal year concept can be traced via simple philology to the well-known series of zp's that frequent the texts of the Old Kingdom if not earlier. A fortiori, it was the event, the occurrence (which we know to be generally one of oxen and small cattle), which formed the basis of the Egyptian numerical reckoning. The latter, although connected with the concept of a year - and a civil year in particular - is to be regarded as at least, ab initio, separate from a collection of 365-days. The economics of Egypt appear to have mattered more to the bureaucrats than the calendrics.
Edel first proceeded along the well-worn path of Gardiner, Sethe, and even Brugsch, by citing a series of useful references to support his case. However, he then added an overlooked Middle Kingdom citation (Amenemhet 1) from Armant8. In an inscription that appears to deal with warlike activity of the king in Nubia, the opening regnal date reads: rnpt zp tpyt nt hcw ...9 Hence, Edel reasoned, the use of the feminine indirect genitive reveals a slightly different situation. In this case the nt can only refer back to the Egyptian word for year, rnpt. This being so, then the only correct (albeit very literal) translation to this passage can be: "first year of the occurrence of the appearance ..." It is the year which is being reckoned (reign of Amenemhet 1) and not the occurrence: rnpt not zp.
A useful parallel to the example brought forward by Edel may be found in the rock inscription (graffito) found at Wadi Handal. There, in a famous yet all-too-brief text dated to Amenemhet I (Zaba's No. 4, cols. 5-8), will be found the following brief notation: "Year 29 of (nt) the King of Upper and Lower Egypt, Shtp-ib-Rc, who lives forever - we came to overthrow Wawat"10. The Egyptian is clear: the regnal date is considered to be feminine (ergo nt) and is connected to the following specific definition of what then occurred in that precise year. In other words, rnpt is the crux word, and as it is feminine, so is the use of the indirect genitive. Hence, with these two references we have reached a period of time in the development of the regnal year system of the Egyptians - Amenemhet 1 at the latest - in which the word "year" and not "occasion" formed the core of the simple term rnpt zp. That it to say, the concept of a census had been totally lost and that a (civil) year took its place. It cannot be overlooked that earlier examples from the Palermo Stone and contemporary documents present such passages as: rnpt ht zp X tnwt. By writing this "year after the Xth occurrence of counting" the cattle count still remained paramount in the minds of the calculator and it is not "regnal year (2X + 1)" that was indicated.
It is also my feeling that the term "regnal year" is somewhat inaccurate when applied to the dates themselves. The enumeration of a Pharaoh's reign, itself based on a year, was originally connected to the counts as often cited. However, when the biennial system had fallen into disuse (although the transference to a simple annual system is not at all easy to locate in time), the translation above, "first year of the occurrence of the appearance ..." points to the persistence of zp as an independent word in the entire phrase. That is to say, "year of the occasion/occurrence/time" renders the ubiquitous rnpt zp far more accurately than regnal year. The latter, after all, stresses the connection to the monarchy whereas the Egyptian words themselves in no way reveal this connotation. For example, it is often claimed that these "regnal years" were signs of royalty and therefore the separate nomarchal dating in the early Middle Kingdom (e.g., at Beni Hasan) indicates some degree of usurpation of royal privilege. Whereas the employ of separate dates by these nomarchs shows heightened private (non-royal) power, let us keep in mind that the two words "regnal year" overtly convey Pharaonic power. A simple "1st year of the appearance" is a better translation as it avoids such connections and more accurately indicates its ancestor of "1st year of the occasion ..."
But it is better to turn to the contemporary regnal year documents from the Old Kingdom (Dynasties 4-6) to enable one to unravel even more the intricacies of dating at this time. The following are all the regnal dates known to me with the Annals included. When the a king's name is absent for whatever reason the object has to be considered with a great deal of caution and, for the most part, I have followed the accepted modern interpretations11.
SNEFRU (Turin Papyrus: 24 years)
(1) "Year of the second occurrence of the count" (Annals, Fragment Cairo No. 4 = Urk. I, 235.17)12. No addition of a cattle sign is present. Following the previous practices recorded in the Annals as outlined above, this reference ought to be placed three years after the commencement year.
(2) "Year of the 7th occurrence of the count" (Annals, Palermo Stone, recto 6 = Urk. I, 236.17). Likewise, no presence of the cattle sign. One reason for the presence of count 7 followed immediately by that of count 8 might be seen in the previous regnal year of Snefru13. At that time the Pharaoh was occupied with a war in Nubia and the regular pattern of a biemiial census could have been interrupted by the king's personal military deeds to the south of Egypt. Hence, I would argue that there was a interruption at this point and the 7th count was delayed by one year owing to the military action to the south. Thereafter, the counts could have resumed their normal biennial regularity with the 8th.
(3) "Year of the 8th occurrence of the count" (Annals, Palermo Stone, recto 7 = Urk. I, 237.4).
(4) "Year of the 15th occurrence" (Red Pyramid of Dashur: Stadelmann, in: MDAIK 43, 1986, 233-35 and Abb. 1). This newly-edited inscription (in hieratic) was located on one of the foundation stones. The association of the date with Snefru is not question able. The lack of tnwt is to be noted: this date is the first clear-cut example that looks as if it were a typical regnal year of a later epoch.
(5) "Year of the 15th occurrence, 2nd month of prt, day 14" (Red Pyramid of Dashur: Stadelmann, in: MDAIK 43, 1986, 234-35 and Abb. 2; see also in: MDAIK 39, 1983, 235, Abb. 6). This brief text was found on one of the backing stones for Snefru's pyramid and provides the first example of a full date in Pharaonic history: year, month, and day are given. The following example is likewise from one of the backing stones.
(6) "Year of the 15th occurrence, 3rd month of Smw, day 10 + x" (Quarry mark at Meidum: Petrie, Meydum and Memphis III, 1910, 9 and PI. V 6). Petrie reads the date as year 17 although his copy indicates otherwise. According to the report, this hieratic inscription as well as others were found, for the most part, on the outermost sloping faces which were rough in texture. The blocks apparently were not dressed down. The dating to Snefru is assured.
(7) Year of the 14 + Xth occurrence" (Quarry mark at Meidum: Petrie, Meydum and Memphis III, 9 and PI. VI 9). The date is unclear: Year 15 or 16 would appear to be the best possibilities.
(8) "Year of the 16th occurrence, 1st month of iht, day 13" (Quarry mark at Meidum: LD II, I g).
(9) "Year of the 16th occurrence, 3rd month of iht" (Red Pyramid of Dashur: Stadelmann, in: MDAIK 43, 1986, 234-35 and Abb. 2; see also in: MDAIK 39, 1983, 235 Abb. 7).
(10) "Year of the 16th occurrence, 4th month of iht, day 14" (Meidum: Rowe, in: The Museum Journal 22, 1931, 26 and PI. XXXVIII, fig. 2). This quarry inscription, as well no. (12), was found by the University Museum in 1929-30.
(11) "Year of the 16th occurrence (?), Xth month of prt, day 2" (Red Pyramid at Dashur: Sourouzian, in: MDAIK 38, 1982, 389-90 and fig. 5). I have placed a query against the regnal year since the integer 15 would fit the arrangement of the signs better than the assumed 16; the facsimile is not all that clear as to which date was intended.
(12) "Year of the 16th occurrence (?), 1st month of prt" (Meidum: Rowe, in: The Museum Journal 22, 1931, 26). The date was questioned by Rowe. Unfortunately, no photograph is given by him in the preliminary report; hence, it is unclear if any day was recorded.
(13) "Year of the 17th occurrence, 2nd month of prt, day 10 + x" (Quarry mark at Meidum: Petrie, Meydum and Memphis III, 9 and PL V 2 left).
(14) "Year of the 17th occurrence, 3rd month of prt, day ..." (Quarry mark at Meidum: Petrie, Meydum and Memphis III, 9 and PI. V 3).
(15) "Year of the 17th occurrence, 3rd month of prt, last day". (Quarry mark at Meidum: Petrie, Meydum and Memphis III, 9 and PI. V 4).
(16) "Year of the 24th occurrence, 3rd (?) month of..." (Red Pyramid of Dashur: Stadelmann, in: MDAIK 43, 1986, 234-36 and Abb. 3). This inscription, originally published by Lepsius and later commented upon by Maystre, forced Stadelmami to hypothesize a rather complicated regnal year dating system for Snefru.
(17) "Year of the 24th occurrence, Xth month of prt, ..." (Red Pyramid of Dashur: Stadelmann, in: MDAIK 43, 1986, 239-40 and Abb. 4). This text, a graffito, was found on one of the outer backing stones of Snefru's pyramid.
It is self-evident that Snefru's dates, as assembled above, do not fit the standard theory of a biennial census - cattle or otherwise. For Stadelmann, one has to subsume some of Snefru's regnal years under the same count, a situation that would render bureaucratic records useless. Quite to the contrary, I feel it best to assume that no biennial census system was employed in a regular fashion at this time. After all, the Palermo Stone is explicit with regard to the 7th and 8th counts, and both of those are written in back-to-back years with the earlier one preceded by a separate year box. It may be argued that the term "year after the Xth count" has not yet come into common use; after all, as I have indicated earlier, the preserved portions of the Annals only record it for the reign of Userkaf. However, there is enough other material (from Helwan and Gebelein) which can be placed into the same time period that contradict this argument.
Connected to the problem of these dates is the lack of any indication concerning what, precisely, they are supposed to signify. In fact, is it correct to assume that all of these rnpt zp dates refer to a "counting" (tnwt) of cattle? Or, as it is easier to hypothesize, are they simple dates identical to the regnal year systems of later epochs? If so, this argument would place the existence of a biemiial cattle census and the earlier ?ms Hr system to the side and therefore neither would confute the data of the Turin Papyrus. That is to say, the 24 years given to Snefru by the last document is not contradicted by the evidence assembled above. The 24-odd "occurrences", therefore, would be equivalent to the evidence in the Turin Papyrus with the absence of a ht 7 in the Palermo Stone indicating that it was not recorded at all - i.e., this designation for a year was omitted. In any case, an analysis of Snefru's dates must be seen in combin ation with others of the 4th Dynasty and it would be rash to draw any conclusion from this evidence alone.
CHEOPS (Turin Papyrus: 23 Years)
(1) "Year of the 4th occurrence, ..." (Back of casing stone in mastaba G 2130 (Hnty-k(i.i)) - Giza, West Field): St. Smith, in: JNES 11, 1952, 118, fig. 6 and 127, no. 4)14. As the author indicates, the "burial in this tomb was accompanied by a sealing with the name of Cheops".
(2) "Year of the 5th occurrence, Xth month of Smw, day ..." (Limestone fragment in the filling of G 1203 (Ki.(i)-nfr - Giza, West Field): St. Smith, in: JNES 11, 1952, 118, fig. 6 and 127, no. 2)15. The date is that of a stone-mason; St. Smith gave cogent reasons why it should be dated to Cheops.
(3) "Year of the 8th occurrence. 1st month of prt, ..." (Cheops Causeway inscription: St. Smith, in: JNES 11, 1952, 119, fig. 7 and 126-27, no. 1). According to St. Smith, the 15th regnal year of the king was intended16.
(4) "Year of the 8th occurrence, 3rd month of Smw, day 20". (Stone mason's graffito, mastaba G 4000 (Hm-Iwnw - Giza, West Field): Junker, Giza I, 1929, 159, Abb. 24, 10 and 161)17. In his brief remarks Junker stressed that the stone work between the core of the mastaba and the (outer) decorative layer/casing must have begun, at the latest, in this year. Moreover, because Junker assumed a biennial system, this was place in year 16.
(5) "Year of the 10th occurrence, 4th month of prt, day 23/24 (?)" (Stone mason's graffito, mastaba G 4000 (Hm-Iwnw - Giza, West Field): Junker, Giza I, 161). This notation is to be found on a fragment in the core of the southern cult chamber.
(6) "Year of the 10th occurrence, 1st month of Smw, day 10" (Stone mason's graffito, mastaba G 4000 (Hm-Iwnw - Giza, West Field): Junker, Giza I, 158, 160 and 159, Abb. 24.1). Junker was not totally sure that "year 10" could be read and felt that an odd year ("after the 10th occurrence") was a possibility.
(7) "Year of the 10th occurrence, 2nd month of Smw, day 10 + X (?)" (Stone mason's graffito, mastaba G 4000 (Hm-Iwnw - Giza, West Field): Junker, Giza I, 159 Abb. 24, 2 and 160).
(8) "Year of the 11th occurrence ..." (Stone mason's inscription on a roofing block in the Cheops' boat pit: Stadelmann, in: MDAIK 43, 1986, 239). This reference has been cited by Stadelmann in conjunction with the reign of Djedefre, Cheops' successor. However, with Helck, I feel that if this citation is valid, then Cheops has to fit18. The reasons for this are simple: (1) the 11th count suits the evidence from the Turin Papyrus indeed, it actually precedes by one the figure in the next inscription, no. 8; (2) the length of Djedefre's reign is unknown but either 11 or 22 years seems quite long; (3) the roofing blocks in the boat pit must have been placed last although the time of their quarrying probably was close to Cheops' death (if not before it); and (4) the pit was probably closed at the time of Cheops interment, and a count of 11 for Djedefre does not suit that timeframe. All in all, even though one may doubt the reliability of this evidence, if the evidence is reliable then one must attribute the date to Cheops.
(9) "Year of the 12th occurrence, 2nd month of Smw". (Inscription on the west wall of the unfinished chapel of G 2120 (SSit-shnt(y)w - Giza, West Field): St. Smith, in: JNES 11, 1952, 118, fig. 6 and 127, 3)19. I follow St. Smith and place this date to the reign of Cheops although Chephren is possible.
A further inscription - a mason's graffito from the mastaba of Hwjw-hcf I - has been placed under Chephren (no. 3). It records the "Year of the 12th occurrence, 2nd month of..." and, as the reader will see from our additional comments, the earlier dating of St. Smith (followed by Simpson) may be more appropriate. It is solely from the recent re-evaluation of Harpur, that have preferred to date the inscription, with much hesitation, under Cheops' second son.
With Cheops we are faced with no real discrepancy: the Turin Papyrus gives 23 years whereas the records reach up to the 12th (An example of a 17th count was argued by Petrie; however, it is probable that he was confused on this matter)20. In this case one may argue for a biennial system. After all, this is a new reign and the practices of Snefru need not have been followed. It is unfortunate that Cairo Fragment No. 2 of the Annals does not preserve any dates and that none of the nine listed cases presents a "year after the Xth occurrence" or any connection with cattle.
DJEDEFRE (Turin Papyrus: length lost)
CHEPHREN (Turin Papyrus: length lost)
(1) "Year of the 2nd occurrence, 4th month of Smw, day 22" (Vertical column on the north subsidiary niche of mastaba G 7530-40 (Mr.s-Cnh III - Giza, East Field): St. Smith, in: JNES 11, 1952, 116, fig. 4 and 126, 2 under A; Dunham-Simpson, The Mastaba of Mersyankh III, 1974, fig. le)21. I follow Reisner and St. Smith in assigning the date to the reign of Chephren but in light of some of the comments of Simpson on pages 3 and 8 of the final publication (following Dunham and Deny), this might have to be revised somewhat22. (The reading of "2" for the year reference seems secure although St. Smith queried it). The text itself seems to present an interval dating on both the right and the left side: "Year of the 2nd occurrence, 4th month of Smw, day 22 to (r) year ... with the left presenting only the following: "(... Xth month of p)rt to year ..." (See as well the fragmentary evidence from the northern subsidiary niche in G 7430-7440 (prince Mnw-hcf- Giza, East Field): St. Smith, in: JNES 11, 1952, 116, fig. 4 and 126, 3 under A).
(2) "Year of the 12th occurrence, 2nd month of Smw, day 10" (Incised inscription on the back of a block of the north wall of the chapel in mastaba G 7650 (iht-fatp and his wife Mrt-it.s - Giza, East Field): St. Smith, in: JNES 11, 1952, 119, fig. 7 and 127-28, 11a)23. The dating follows that of St. Smith even though no royal name is present.
(3) "Year of the 12th occurrence, 2nd month of..." (Inscription on the east face of a block originally from mastaba G 7130-40 (Hwfw-hcf\ - Giza, East Field): St. Smith, in: JNES 11, 1952, 119, fig. 7 and 127, 8 = Simpson, The Mastabas of Kawab, Khafkhufu I and II (1978), 9 and fig. 35c)24. This block most certainly originally belonged to part of the east face of Hwfw-hcf I's mastaba although it now belongs to part of the projecting temple of Isis. There is a second inscription that preserves only the following: "... 2nd month of prt, day ..." If Harpur's date for the mastaba is followed, one may wish to place this inscription under Chephren. Simpson, however, following St. Smith, opted for Cheops. Hence, the attribution is not completely sucure.
(4) "Year of the 13th occurrence, 4th month of..." (Painted date on the back of a casing stone on the north face of mastaba G 7650: St. Smith, in: JNES 11, 1952, 119, fig. 7 and 127-28, 11b).
The following six dates, all from Helwan, perhaps can be added at this point. Even though their association with any king is impossible to determine, the palaeography points to a late Dynasty 4-first half Dynasty 5 date and the presence of the name of Chephren's pyramid (the first example below) serves as a somewhat useful terminus a quo25. With much hesitation, and more for the sake of convenience, I have placed them at this point.
(i) "Year of the 1st occurrence, 4th month of iht, day 5" (Hieratic stone ostracon from tomb 299 H 2 at Helwan: Saad, Royal Excavations at Saqqara and Helwan (1941-1945), 1947, 106 and PI. 42a left; Cairo JdE 86854 B). According to Fischer, these inscribed stone pieces served as identification labels for the bodies that were sent north from Upper Egypt in order to be interred at the cemetery of Helwan. Although the photograph of this ostracon is not overly clear, the presence of the king's cartouche preceded by the date clinches the reference.
(ii) "Year after the 4th occurrence of the count, 2nd month of Smw, day 3" (Hieratic stone ostracon from tomb 305 H 2 at Helwan: Saad, Royal Excavations at Saqqara and Helwan (1941-1945), 106-107 and P. XLIIb right; Cairo JdE 86853 A. A second ostracon (Saad, ibid., PI. XLIIb left; Cairo JdE 86853 B) is somewhat broken and the reference to the day is lost). In these two cases we have: rnpt ht zp 4 tnwt ... Hence, these two ostraca not only reveal an early use of a "Year after the Xth occurrence" system but, perhaps more importantly, add tnwt, thereby indicating that the "count" was in operation and that it still could be written with regnal years.
The Egyptian term rnpt ht zp, which is employed here (instead of rnpt m ht zp X) might be of some use for dating purposes. Edel, however, indicated that both occur throughout the Old Kingdom26. A useful list of these readings will be presented in the analysis of undated 6th Dynasty inscriptions (pages 46-47 below).
(iii) "Year after (= rnpt hi) the 5th occurrence, 2nd month of Smw, day 8" (Hieratic stone ostracon from tomb 322 H 2 at Helwan: Saad, ibid., 107 and PI. XLIIIa right; Cairo 86852 B). The reading of the year is unclear. Although Goedicke prefers "5", the ostracon iv following presents a clear-cut case of that numeral and the hieratic is considerably different that the one from tomb 322 H 227. In addition, note the lack of tnwt, "count".
(iv) "Year after (= rnpt ht) the 5th occurrence, 2nd month of Smw, day 8" (Hieratic stone ostracon from tomb 335 H 2 at Helwan: Saad, ibid., 107 and PI. XLIIIa right; Cairo 86852 B). The hieratic inscription is virtually impossible to read but the format would have been identical to the preceding.
(v) "Year of the 5th occurrence, 3rd month of prt, day 22." (Hieratic stone ostracon from tomb 335 H 2 at Helwan: Saad, ibid., 107 and PI. XLIIIb right; Cairo JdE 86851 A).
(vi) "Year of the ...th (occurrence), ..." (Hieratic stone ostracon from tomb 335 H 2 at Helwan: Saad, ibid., 107 and PI. XLIIIb left; Cairo JdE 86851 B). The text is very abraded but it would have repeated the previous one.
With Chephren the lacuna in the Turin Papyrus is particularly troublesome as one may opt for 26 regnal years (or even higher) if the biennial hypothesis is adhered to. On the other hand, others may prefer 13 years for his reign with, perhaps, a few more. Nothing definitive can be determined from these data so far as it stands. The Helwan material, on the other hand, ambiguous though it may be, at least indicates that the counts were operating, so long as all of the ostraca can be placed to this reign. From the position of hieratic palaeography this is unsure28.
MYCERINUS (Turin Papyrus: 18, possibly 28; 38 years is doubtful)
(1) "Year of the 1st occurrence, 1st mondi of Smw, day 21." (Vertical inscription from mastaba G 7530-40 (Mr.s-Cnh III - Giza, East Field): St. Smith, in: JNES 11, 1952, 116, fig. 4 and 126, 1; Dunham-Simpson, The Mastaba of Mersyankh III, 8 and PI. Ha, fig. 2). The recent publication of Dunham-Simpson revises the older position of Reisner29. Instead of locating this reference and the one following to the reign of Shepseskaf, they prefer Mycerinus on the basis of Derry's examination of the bones of Mr.s-Cnh. Gardiner, in: JEA 31, 1945, 14-15 and note 3, altered some of Reisner's comments through his support of the biennial census theory. The elapsed time of 272 days between death (example 1) and burial (2) does seem high. The year is not written with the tpy sign30.
(2) "Year after the 1st occurrence, 2nd month of prt, day 21." (Vertical inscription from mastaba G 7530-40 (Mr.s-Cnh III - Giza, East Field): references as in the previous example). This is the internment date for queen Mr.s-Cnh. Here, the tpy sign is em ployed: rnpt ht zp tpy. The m in a possible rnpt m ht may have been dropped owing to the vertical nature of the composition.
(3) "Year of the 2nd occurrence, 2nd month of prt, day 22." (Quarry graffito on a north block of mastaba G VI S, Junker's VII (Giza - West Field): Junker, Giza X, 1951, 75, Abb. 35.9 and 78, no. 10; see also Junker, Anz.AWW 1929, 82)31. The dating to Mycerinus is derived from the names of the work crews on other associated masons' graffiti; see case (6) below. (NB: this argument is not that compelling).
(4) "Year of the 7th occurrence, 4th month of prt, day 10" (Quarry mark on casing stone of mastaba G 7530-7540 (Mr.s-Cnh III - Giza, East Field): St. Smith, in: JNES 11, 1952, 119, fig. 7 and 127, 9; Dunham-Simpson, The Mastaba of Mersyankh III, 3 and fig. 1). This date was reassigned by Dunham-Simpson to the reign of Mycerinus instead of Chephren, as Reisner believed.
(5) "Year of the 10th occurrence, 3rd month of Smw, ..." (Stone mason's graffito in mastaba G 7350 (Htp-hr.s II (?) - Giza, East Field): St. Smith, in: JNES 11, 1952, 119 fig 7 and 127, 10). This date was tentatively assigned to Mycerinus by St. Smith; Harpur dates the time period of the tomb to the end of Dynasty 4 (Khaefre to Shepseskaf)32. This attribution is tentative.
(6) "Year of the 11th occurrence, Xth month of prt, day 10 + X" (Quarry inscription on a block of mastaba G VI S, Junker's VII (Giza, West Field): Junker, Giza X, 1951, 75, Abb. 35.10 and 77, no. 9; see Junker, Anz.AWW 1929, 82). This hieratic mark, like no (3) above, is dated to Mycerinus by association33. A further date has been signaled by Helck, but it possesses no associated cartouche34. In fact, a better timeframe appears to be the end of Dynasty 5:
(i) "Year of the 11th (?) occurrence, 3rd month of prt, day 3 (?)" (Stone mason's graffito associated with Shaft S 677/817 (Giza, West Field): Junker, Giza VIII, 1947, 39-40, with Abb. 12). Since there is no king's name associated with this inscription the dating is insecure; Helck prefers Mycerinus. (I suspect that he confused this quarry mark and the one published by Junker in Giza X: no. 6 above). Harpur dated the associated mastaba of Rc-wr II (G 5470) to the end of Dynasty 5 (Izezi-Unis)35. As the blocks themselves are located in the serdab of Rc-wr II's mastaba, the small inscription is best placed to that period. Junker, perhaps most wisely, refused to pinpoint a date, and correctly dismissed the evidence of a sealing of Dd-ki-Rc (Izezi) in mastaba G 547036. This inscription will be mentioned again at the end of the Dynasty 5 examples.
If the attribution of any of the last three texts to Mycerinus is correct then one might have to revise the Turin Papyrus' presumed "year 18" to "year 28". In the case of Mycerinus, however, the epigraphic evidence of a datable sort is so scarce that any conclusions must be of a tentative nature. The first two cases, signaled with great vigor by Gardiner, are the most important, if correctly placed to Mycerinus' reign. They provide the only case of one year succeeding another and the presence of the "after" (hi), is useful mark that some type of count was still understood.
To be added here is the evidence from the papyri at Gebelein. These have not yet been published as a unit although preliminary reports have come from the hand of Posener-Krteger37. A date in Dynasty 4 for the lot is certain. The following examples are concerned with dates that include the year.
(i) "(Year) after (= rnpt m hi) the 2nd occurrence of the count of cattle (of Upper and Lower Egypt, Xth month of) iht, day 20" (Gebelein fragment A: Posener-Krteger, Les prix des 6toffes, in Fs Edel, 318-31).
(ii) "Year after (= rnpt m hi) the 3rd occurrence of the count of cattle of Upper and Lower Egypt, 3rd month of prt, day 26" (Gebelein fragment B: Posener-Krteger, ibid).
(iii) "Year after (= rnpt m hi) the 11th count." (Gebelein Roll IV, Cairo JdE 66844, 4: Posener-Krteger, in: RdE 27, 1975, 215-16). If we assume that a biennial system is reflected in this count, then since the palaeography definitely indicates a date before the Abusir archive, this moves us back to Dynasty 4. In fact, the editor did take into account the strong possibility that the papyrus might be placed into the reign of Mycerinus but probably not earlier38. On the other hand, if the biennial system is disregarded, then Niuserre (improbable), Sahure, and Mycerinus could fit. I do not see the chance that this new archive can be placed to the reign of Unis, after the major group at Abusir. In fact, in Posener-Krteger's chart of palaeographic comparisons there is little doubt that the Gebelein group are earlier than Abusir, and Goedicke was correct to place the fragments in the 4th Dynasty39.
SHEPSESKAF (Turin Papyrus: length lost or 2 years?)
(1) "Year ... of the Unification of Upper and Lower Egypt" (Annals, Palermo Stone, verso, line 1 = Urk. I, 239.12). This is not the "year of the first occasion; the latter is: rnpt zp 1. The importance of the date, the accession year, was discussed by Borchardt and Gardiner in connection with the switch from Shepseskaf s predecessor to himself40. It is crucial to make this difference: the first year of a Pharaoh - which for all practical purposes was less than 365 days - was, at this time, not numbered. This we have already seen from the evidence on the recto of the Palermo Stone and Cairo Fragment No. 1. Both of those pieces have the biennial Sms Hr celebration (reigns of Smerkhet and Djoser) located after the opening accession year.
(2) "Year after the 1st occurrence of count of (all) oxen and small cattle" (Edict of Shepseskaf for the Pyramid of Mycerinus: Goedicke, KOnigl. Dokumente, 16, 17, Abb. 1 = Urk. I, 160). In this interesting case two points are useful to stress. First, the term employed for the term "count" is ipt and not tnwt, as previously41. Indeed, this is the first explicitly dated inscription that employs this word in any of the extant Old Kingdom documents that are dated. A further case, unfortunately not securely fixed to a reign (although Chephren and Mycerinus do fit the timeframe), is presented as case (vi) of the insecure texts of Dynasty 4. (The text is the will of Ni-kiw-cnh). Second, the determinatives (unless they were read) of ipt are the oxen and small cattle: i.e., all basic bovine herds are included; this occurs infrequently and should not be overstressed and also occurs in Ni-kiw-cnKs will as well as in some others of Dynasty 5 (e.g., (2) of Djedkare). Finally, the Egyptian phrase for "year after" is rnpt m ht.
(2) "Year of the 2nd occurrence, 2nd month of prt, day 10 (?)" (Limestone fragment found in debris of shaft (C) of mastaba G 5080 (SSm-nfr II - Giza, West Field): St. Smith, in: JNES 11, 1952, 120 and 127, 5)42. The attribution of this fragment to Shepseskaf is unclear. St. Smith argued that since a sealing of that ruler was found in $sm-nfr II's burial chamber, it was possible that he is to be connected with this date. This argument is not compelling. In fact, since SSm-nfr II's mastaba was built and decorated during the reign of Niuserre, it is more probable that the piece belongs to his reign than Shepseskaf s. For this reason, I have placed this case under Niuserre's reign as well.
If the last example is correctly dated to Shepseskaf s second count then the above three references provide a useful though all-too-short series of opening years' dates. Because Dunham and Simpson cast doubt on the attribution of two vertical faxade texts of mastaba G 7530-40 (Mr.s-Cnh III) to Shepseskaf, preferring instead Mycerinus, two other extremely useful dates have to be ignored here43. This conclusion is doubly distressing as both of them can be placed in "count 1" and the year immediately after. Hence, they would have rounded out the early regnal years of Shepseskaf to a full degree: opening year; count 1; year after count 1 (twice); and count 2. As the number of years which he sat upon the throne of Egypt is unknown - it is normally argued that they were few none of these cases is egregious.
Some unplaced Dynasty 4 texts may be added to the above list. The following are provided here although there is no absolute reason to locate them to this Dynasty.
(i) "Year of Unification of the Two Lands, 2nd month of Smw, day 10" (Incised limestone block under mastaba G 2359 = G 5552 (Giza, West Field): St. Smith, in: JNES 11, 1952, 118, fig. 6 and 127, 7). The author's doubts are best expressed in his own words. The object is "Perhaps a Fourth Dynasty construction block abandoned for some reason on the edge of the Western Cemetery"44. Nevertheless, it is useful to have the accession year of a king recorded outside of the Annals and on a contemporary inscription. NB: unlike the Annals the date reads rnpt smi tiwy, this is also present in Wp-m-nfris will which is placed (with much hesitation) under Unis, one text of Dynasty 8 (an edict: no. 1) as well as the three inscriptions that follow.
(ii) "Year of the Unification of the Two Lands, 3rd month of Smw, day ..." (Stone block with inscription: James, Corpus of Hieroglyphic Inscriptions in the Brooklyn Museum I, 1974, 22-23 and PI. XXIII (No. 58a) = Urk. I, 10.14). The import of this short text eludes me; for the possible association with Nfab-kiw, see Simpson in: AJA 79, 1975, 153. However, as that feast occurred on 1 prt 1 no equivalence is possible. I agree with Simpson that the Brooklyn piece is undoubtedly the same object from which the Berlin Abdruck 1189b was taken. With hesitation, but still following Simpson, I place the object to Dynasty 4.
(iii) "Year of the Unification of the Two Lands, 3rd month of Smw, (day) ..." (Limestone fragment found in the debris of mastaba G 7450 (Giza, East Field): St. Smith, in: JNES 11, 1952, 120, fig 8 and 128)45. This piece was brought forward as additional evidence by Simpson in his discussion of the preceding inscription. The coincidence of year and month is to be stressed.
A further parallel text is the following:
(iv) "Year of the Unification of the Two Lands, 4th month of Smw, day 4" (Berlin 14467: Schafer, Berl. Inschr. I, 1913, 71 = Urk. I, 10.14).
(v) "Year of the 10th occurrence, 4th month of iht, day 24" (Ostracon Leiden J 429: Goedicke, in: JEA 54, 1968, 28-30 and PI. V 4). Goedicke believes that what is recorded here is the death of an individual and a date close to the five Helwan examples listed above seems reasonable. (Indeed, this is what he later assumed in his volume on Old Kingdom Palaeography as he dated the Helwan ostracon as well as those in Leiden contemporary to the Gebelein papyri)46. In his edition of this ostraca and three others Goedicke appears to place the object to the close of Dynasty 4-early Dynasty 5. If the biennial nature of the count is taken seriously, then a date in the reigns of Cheops or Niuserre seems reasonable. Those rulers intervening either are given less than 20 years by the Turin Canon (e.g., Userkaf and Sahure) or else the length of their reigns is unclear. I, myself, would leave the question open, preferring to deal with the presence of such counts independently of the question of any biennial system.
(vi) "Year of the 12th occasion of count of (all) oxen and small cattle" (Will of Ni-kiw-Rc in mastaba LG 87 (Giza, Central Field): Goedicke, Die privaten Rechts inschriften, 1970, 21 and PI. lib with 22, note 1 = Urk. I, 16.14)47. In this case the reigning king is unclear. The mastaba, however, can be placed to the close of Dynasty 4: Harpur, for example, prefers Chephren to Shepseskaf. With such a high regnal year in his will only Chephren or Mycerinus are possible, and I would opt for the latter simply because the art historical criteria cover at least three reigns. Moreover, the presence of the word ipt, already commented upon twice by Goedicke, parallels the case of the Edict of Shepseskaf listed above (example (2) in his reign)48. He saw the disappearance of tnwt as perhaps indicative of an alteration that occurred with the beginning of the 5th Dynasty. However, tnwt does occur earlier, as the Annals indicate. Certainly, the regularity that we expect on the part of the numbering system in the Old Kingdom is not present on these two occasions. The hypothesis of a regularly-occurring and standardized biennial cattle census, always marked with tnwt, does not receive much support from the texts themselves.