The Problem of the Magical Squares according to the Indians, Excerpt from "A New Historical Relation of the Kingdom of Siam"
Tome II
by Monsieur De La Loubere
Envoy Extraordinary from the French King, to the King of Siam, in the years 1687 and 1688. Wherein a full and curious Account is given of the Chinese Way of Arithmetick, and Mathematick Learning. In Two Tomes, Illustrated with Sculptures. Done out of French, by A.P. Gen. R.S.S.
1693
Cassini is also credited with introducing Indian Astronomy to Europe. In 1688, the French envoy to Siam (Thailand), Simon de la Loubère, returned to Paris with an obscure manuscript relating to the astronomical traditions of that country, along with a French translation. The Siamese Manuscript, as it is now called, somehow fell into Cassini's hands. He was intrigued enough by it to spend considerable time and effort deciphering its cryptic contents, also determining on the way that the document originated in India. His explication of the manuscript appeared in La Loubère's book on the Kingdom of Siam in 1691.
-- Giovanni Domenico Cassini, by Wikipedia
Curiously enough the first definite information respecting the Hindu system of astronomy, came to Europe from Siam, where, in the early centuries of our era, there was a flourishing Hindu state. In 1687 Louis XIV sent M. de la Loubere on an embassy to Siam, and he brought back with him a portion of a manuscript containing rules for computing the places of the sun and moon. This was submitted to the celebrated John Dominic Cassini, the Italian astronomer, whom Louis had brought to Paris to take charge of his observatory. In his hands the calculations described, without indication of the meaning of the constants employed, were lucidly explained.
-- Burgess, James (1893). "Notes on Hindu Astronomy and the History of Our Knowledge of It". Journal of the Royal Asiatic Society of Great Britain & Ireland: 722–723.
I gave to Mr. Cassini, Director of the Observatory at Paris, the Siamese Method of finding the place of the Sun and Moon by a Calculation, the ground of which is taken from this Epocha. And the singular Merit which Mr. Cassini has had of unfolding a thing so difficult, and penetrating the Reasons thereof, will doubtless be admired by all the Learned. Now as this Epocha is visibly the ground only of an Astronomical Calculation, and has been chosen rather than another, only because it appear'd more commodious to Calculation than another, it is evident that we must thence conclude nothing which respects the Siamese History; nor imagine that the Year 638, has been more Famous amongst them than another for any Event, from which they have thought fit to begin to compute their Years, as we compute ours, from the Birth of the Saviour of the World.
-- CHAP. XI. What the Siameses do know of the Mathematics. Excerpt from "A New Historical Relation of the Kingdom of Siam", Tome II, by Monsieur De La Loubere, Envoy Extraordinary from the French King, to the King of Siam, in the years 1687 and 1688. Wherein a full and curious Account is given of the Chinese Way of Arithmetick, and Mathematick Learning. In Two Tomes, Illustrated with Sculptures. Done out of French, by A.P. Gen. R.S.S., 1693
Tome II, p. 227-247
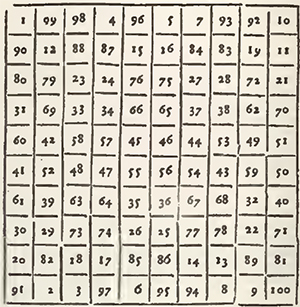
The Problem of the Magical Squares according to the Indians.
This Problem is thus:
A square being divided into as many little equal figures as shall be desired, it is necessary to fill the little squares with as many numbers given in Arithmetical progression, in such a manner that the numbers of the little squares of each rank, whether from top to bottom, or from right to left, and those of the Diagonals do always make the same sum.
Now to the end that a square might be divided into little equal squares, it is necessary that there are as many ranks of little squares, as there shall be little squares to each rank.
The little squares I will case the cases, and the rows from top to bottom upright, and those from right to left transverse; and the word rank shall equally denote the upright and transverse.
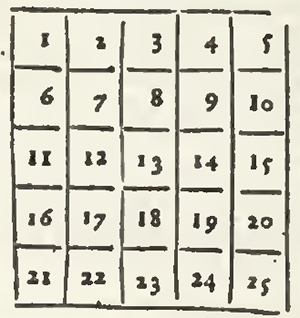
I have said that the Cases must be filled with numbers in Arithmetical progression, and because that all Arithmetical Progression is indifferent for this Problem, I will take the natural for example, and will take the Unite for the first number of the progression.
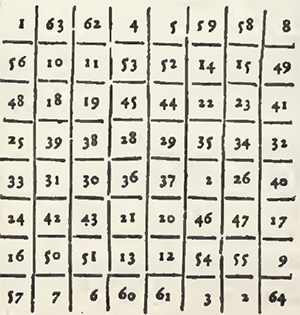
Behold then the two first examples, viz. the square of nine Cases, and that of 16, filled, the one with the nine first numbers from the unite to nine, and the other with the sixteen first numbers from the unite to 16: So that in the square of 9 Cases, the summ of every upright, and that of every Transverse is 15, and that of each Diagonal 15 also: and that in that of 16 Cases, the summ of every upright, and that of every Transverse is 34, and that of each Diagonal 34 also.
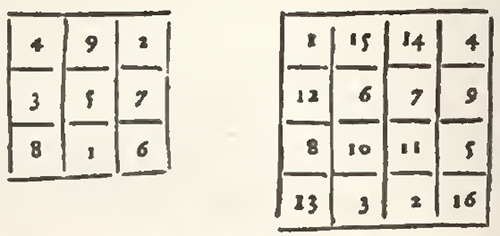
This Problem is called Magical Squares, because that Agrippa in his second Book De Occulta Philosophia, cap. 22. informs us that "they were used as Talismans, after having engraved them on plates of diverse metals: the cunning that there is in ranging the numbers after this manner, having appear'd so marvellous to the ignorant, as to attribute the Invention thereof to Spirits superior to man. Agrippa has not only given the two preceding Squares, but five successively, which are those of 25, 36, 49, 64, and 81 Cases; and he reports that these seven squares were consecrated to the seven Planets. The Arithmeticians of these times have looked upon them as an Arithmetical sport, and not as a mystery of Magic. And they have sought out general methods to range them.
The first that I know who laboured therein, was Gaspar Bachet de Meziriac, a Mathematician famous for his learned Commentaries on Diophantus. He found out an ingenious method for the unequal squares, that is to say, for those that have a number of unequal cases: but for the equal squares he could find none. 'Tis in a Book in Octave, which he has entitled, Pleasant Problems by numbers.
Mr. Vincent, whom I have so often mentioned in my Relation, seeing me one day in the Ship, during our return, studiously to range the Magical squares after the manner of Bachet, informed me that the Indians of Suratte ranged them with much more facility, and taught me their method for the unequal squares only, having, he said, forgot that of the equal.
The first square, which is that of 9 cases, return'd to the square of Agrippa, it was only subverted: but the other unequal squares were essentially different from those of Agrippa. He ranged the numbers in the cases immediately, and without hesitation; and I hope that it will not be unacceptable that I give the Rules, and the demonstration of this method, which is surprizing for its extream facility to execute a thing, which has appeared difficult to all our Mathematicians.
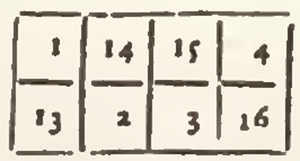
1. After having divided the total square into its little squares, they place the numbers according to their natural order, I would say by beginning with the unite, and continuing with 2, 3, 4, and all the other numbers successively, and they place the unite, or the first number of the Arithmetical Progression given, in the middle case of the upper transverse.
2. When they have put a number into the highest case of an upright, they place the following number in the lowest case of the upright, which follows towards the right: that is to say, that from the upper transverse they descend immediately to that below.
3. When they have placed a number in the last case of a transverse, the following is put in the first case of the transverse immediately superior, that is to say, that from the last upright, they return immediately to the first upright on the left.
4. In every other occurrence, after having placed a number, they place the following in the cases which follow diametrically or slantingly from the bottom to the top, and from the left to the right, until they come to one of the cases of the upper transverse, or of the last upright to the right.
5. When they find the way stopp'd by any case already filled with any number, then they take the case immediately under that which they have filled, and they continue it as before, diametrically from the bottom to the top, and from the left to the right.
These few Rules, easie to retain, are sufficient to range all the unequal squares in general. An example tenders them more intelligible.
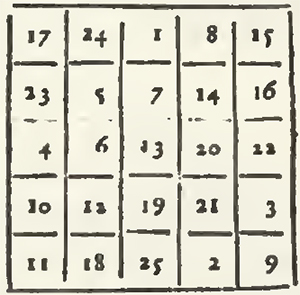
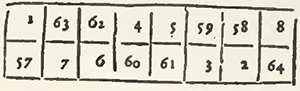
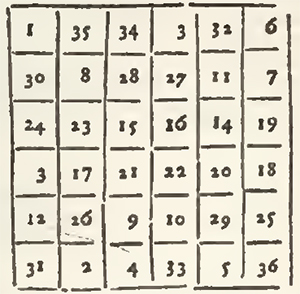
This square is essentially different from that of Agrippa; and the method of Bachet is not easily accommodated thereto; and on the contrary, the Indian method may easily give the squares of Agrippa, by changing it in something.
1. They place the unite in the Case, which is immediately under that of the Center, and they pursue it diametrically from top to bottom, and from the left to the right.
2. From the lowest case of an upright, they pass to the highest case of the upright which follows on the right; and from the last case of a Transverse they return to the left to the first case of the Transverse immediately inferior.
3. When the way is interrupted, they re-assume two cases underneath that which they filled; and if there remains no case underneath, or that there remains but one, the first case of the upright is thought to return in order after the last; as if it was indeed underneath the lowest.
An Example taken from Agrippa.
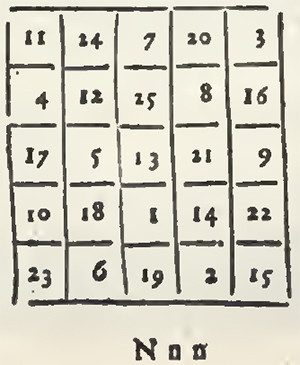
As Bachet has not given the demonstration of his method, I have search'd it out, not doubting but it would give me also that of the Indian method: But to make my demonstration understood, it is necessary that I give the method of Bachet.
1. The square being divided by cases, to be filled with numbers in the Magical order, he augments it before all things by the square sides in this manner. To the upper part of the first transverse, he adds another transverse, but contracted by two cases, viz. one at each end. Over this first transverse contracted he adds a second contracted by two new cases. To the second he adds a third more contracted than the former, to the third a fourth, and so on, if it is necessary, until that the last transverse have but one case. Underneath the last transverse he adds likewise as many transverses more contracted one than the other. And in fine, to the first upright on the left, to the last upright on the right, he adds also as many uprights thus contracted.
EXAMPLES.
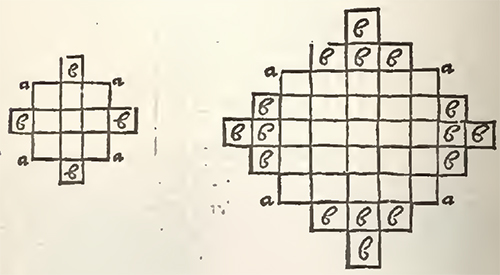
aa are the squares of 9 and 25 cases, bb are the cases of Augmentation.
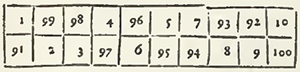
The square being thus augmented, Bachet there places the numbers according to the natural order, as well of the numbers as the cases, in the following manner.
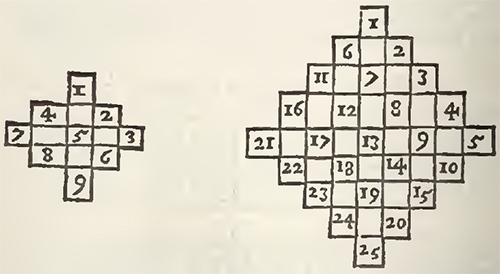
In this disposition it is evident that the cases of the true square are alternately full, and alternately empty, and that its two Diameters are entirely full. Now the full cases receive not any change in the sequel of the operation, and the Diameters remain always such as they are by position in the square augmented: but for the cases of the true square, which are likewise void, they must be filled with the numbers which are in the cases of Augmentation, by transporting the high ones lower, and the low ones higher, each into its upright; those of the right to the left, and those of the left to the right, each into its transverse, and all to as many cases, as there are in the side of the real square. Thus in the square of 9 cases, which has only three in its side, the unite, which is in the case of Augmentation at the top, is removed to the third case below in the same upright; 9, which is in the case of Augmentation below, is removed to the third case above in the same upright, [illegible], which is in the case of Augmentation on the right, is remov'd toward the left, to the third case in the same transverse; and in sine, 7, which is in the case of Augmentation on the left, is removed towards the right, to the third case in the same transverse.
After the same manner, in the square of 25 cases, which has 5 in its side, the numbers, which are in the cases of Augmentation above, do descend 5 cases below each in its upright. Those of the cases of Augmentation below do ascend five cases above each in its upright. Those of the cases of Augmentation on the right do pass 5 cases to the left, each in its transverse; and those of the cases of Augmentation on the left do pass 5 cases to the right, each also in its transverse. It ought to be the same in all the other squares proportionably, and thereby they will become all Magical.
Definitions.
In the augmented square of Bachet, the ranks of Augmentation shall be called Complements of the ranks of the true square, into which the numbers of the ranks of Augmentation must be removed: and the ranks which must receive the Complements, shall be called defective ranks. Now as by Bachet's method every number of the cases of Augmentation must be removed to as many cases as there are in the side of the true square, it follows that every defective rank is as far distant from its Complements, as there are cases in the side of the true square.
2. Because that the true square, that is to say, that which it is necessary to fill with numbers according to the Magical Order, is always comprehended in the square augmented, I will consider it in the square augmented, and I will call its ranks and its diameters, the ranks and diameters of the true square; but its ranks, whether transverse or upright, shall comprehend the cases, which they have at both ends; because that the numbers which are in the cases of Augmentation, proceed neither from their transverse nor from their upright, when removed into the cases of the true square, according to Bachet's method.
3. The diameters of the square augmented are the middle upright, and middle transverse of the true square, and they are the sole ranks which are not defective, and which receive no complement. They neither acquire, nor lose any number in Bachet's operation: they suffer only the removal of their numbers from some of their cases into others.
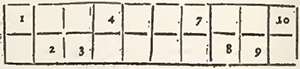
4. As the augmented square has ranks of another construction than are the ranks of the true square, I will call them Bands and Bars. The Bands descend from the left to the right, as that wherein are the numbers 1, 2, 3, 4, 5, in the preceding example, the Bars descend from the right to the left, as that, wherein are the numbers 1, 6, 11, 16, 11, in the same example.
Preparation to the Demonstration
The Problems of the Magical squares consists in two things.
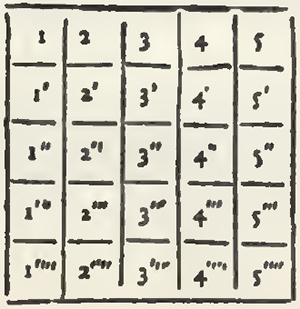
The first is that every transverse and every upright make the same sum, and the second that ever diameter make likewise that same sum. I shall not speak at present of this last condition, no more than if I sought it not. And because that to arrive at the first, it is not necessary that all the numbers, which ought to fill a Magical square, be in Arithmetical proportion continued, but that it suffices that the numbers of a Band be Arithmetically proportional to those of every other Band, I will denote the first numbers of every Band by the letters of the Latin Alphabet, and the differences between the numbers of the same Band by the letters of the Greek Alphabet; and to the end that the numbers of a Band be Arithmetically proportional to the numbers of every other Band, I will set down:
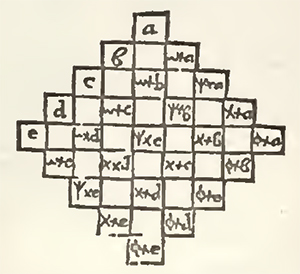
the differences of the numbers of each band by the same Greek Letters.
1. Nothing hinders why the Sign -, may not be placed instead of the Sign +, either before all the differences, or before some, provided that the same Sign be before the same difference in each band: for so the Arithmetical proportion will not be altered.
2. The greater a square shall be, the more Latin and Greek Letters it will have; but every band will never have but one Latin Letter, and all the Greek Letters; and the Latin Letter shall be different in each band. Every bar on the contrary shall have all the Latin Letters, and all except the first shall have a Greek Letter, which shall be different in every bar.
Demonstration.
From hence it follows. 1. That the diameters of the augmented square have each all of the Latin and all the Greek Letters, because that they have each a case of every band, and a case of every bar, and that the cases of every band do give them all the Latin Letters, and the cases of each bar all the Greek. The sum then of these two diameters is the same, viz. that of all the Letters, as well Greek as Latin, taken at once. Now these two diameters do make an upright and a transverse in the Magical square, because that in the operation of Bachet, their sum changes not by the loss or acquisition of any number, as I have already remarked.
2. As the ranks of the true square, whether transverse or upright, are as distant from their complements, as there are cases in the side of the true square, it follows that the bands, and the bars, which begin with a complement, or above this complement, touch not, that is to say, have no case at the defective rank of this complement; and that the bands and the bars which begin with a defective rank or above, have no case in its complement: the Letters then of the defective rank, are all different from those of the complements; because that different bands have different Latin Letters, and that different bars have different Greek Letters. But because that all the bands, and all the bars, have each a case in all the defective ranks, or in their complements: then every defective rank whatever, will have all the Letters, when it shall have received its complement; it will have all the Latin, because that all the bands, passing through every defective rank, or through its complement, do there leave all the Latin Letters; and it will have all the Greek, because that all the bars, passing also through every defective rank, or through its complement, do there leave all the Greek Letters. And thus all the defective ranks will make the same sum in the Magical square, and the same sum as the diameters of the square augmented, which are the two sole ranks not defective of the true square.
That this Method cannot agree to even Squares.
The Demonstration which I have given, agrees to the equal squares, as well as to the unequal, in this that in the augmented equal square, every defective rank and its complement do make the sum, which a range of the Magical square ought to make: But there is this inconvenience to the equal squares, that the numbers of the cases of Augmentation, do find the cases of the true square filled with other numbers, which they ought to fill; because that every case is full, which goes in an equal rank after a full case, and that in the equal squares, the cases of the defective ranks do come in an equal rank, after those of the complements, the defective ranks being as remote from the complements, as the side of the square has cases, and the side of every equal square having its cases in equal number.
Of the Diameters of the unequal Magical Squares.
By Bachet's operation it is clear, that he understands that the diameters are such as they ought to be, by the sole position of the numbers in the augmented square: and this will be always true, provided only that it is supposed, that the number of the case of the middle of each band, be a mean Arithmetic proportion between the other numbers of the same band, taken two by two: a condition, which is naturally included in the ordinary Problem of the Magical squares, wherein it is demanded that all the numbers be in Arithmetical proportion continued. Alternato the mean number of each bar, will be also a mean Arithmetical proportional between all the numbers of the same bar taken two by two: and hereby every mean, taken as many times as there are cases in the band, or in the bar, which is all one, will be equal to the total sum of the band, or of the bar. Therefore all the means of the bands, taken as many times as there are cases in every band, or which is all one, in the side of the square, will be equal to the total sum of the square: then taken once only, they will be equal to the sum of one of the ranks of the Magical square; and it will be the same of the means of the bars: and because that the means of the bands do make one diameter, and the means of the bars the other, it is proved that the diameters will be exact by the sole position of the numbers in the augmented square, provided that every mean of a band, be a mean Arithmetic proportional between all the numbers of its band, taken two by two.
In a word, as in the squares there are no augmented pairs, nor true square nor diameters of the true square, because that the bands of the equal squires have not a mean number, 'tis likewise a reason, which evinces that this method, cannot be accommodated to the equal squares.
Methods of varying the Magical Squares by Bachet's Square augmented.
1. By varying the order of the numbers in the bands, or in the bars, provided that the order which shall be taken, be the same in all the bands, or the same in all the bars, to the end that in this order the numbers of a band or of a bar, be Arithmetically proportioned to those of every other band or bar: but it is necessary that not any of the diameters loses any of its numbers.
2. Or rather (which will amount to the same) by varying the order of the bars amongst them in the augmented square: for this troubles not the Arithmetical proportion, which is the ground of the preceding demonstration: but it is necessary to remember to leave always in their place the band and the bar, which do make the two diameters.
3. By not putting the first number of each band, in the first case of each band: As for example

d, a, e, c, b, are the five letters of the first band, the order of which is arbitrary, and the letter d, which is in the first case of this first band, is not found in the first case of any other band 2 + but in the fourth case of the second band, in the second of the third, in the fifth of the fourth, and in the third of the fifth. Besides the succession or other of the Letters must be the same in every band. But because that in the bands where the Letter d is in a case lower than the first, there remains not case enough underneath, to put all the other Letters successively, the first cases of the bands do return in order after the last, and are in this case thought the last cases of their bands. A circumstance which it is necessary carefully to observe.
If then in an augmented square the numbers are disposed in each band, as in the bands of this square I have disposed the Letters a, b, c, d, e, and which one continues to operate like Bachet, that is to say, to remove as he does, the numbers of the cases of Augmentation into the void cases of the real square, the true square will be Magical, at least as to the ranks, whether transverse or upright, for I speak not as yet of the Diameters.
I shall call those capital cases, wherein are found the Letters like to the Letter which is put in the first case of the first band, which I will call the first capital case.
Preparation to the Demonstration.
1. It is necessary to observe in disposing these Letters, that after having chosen the capital case of the second band, near a Letter of the first band, which I will call the Letter of Indication, so that this second capital case be also the second case of the bar which begins with this Letter of Indication, one may chuse the capital case of the third band, near the Letter of the second band, like to the first Letter of Indication, so that this third capital case be the third of the bar, wherein shall be the second Letter of Indication. After the same manner shall be determin'd the capital case of every band, near the Letter of Indication of the precedent band. From whence it follows, that there are as many capital cases as bands, and no more.
It follows also, that not only the Letter d is always under the Letter c in the same bar, but that all the other Letters are always under the same Letters in the same bars, and that the Letters have likewise the same order in all the bars, as they have the same in all the bands, though the orders of the Letters in the bars, is not the same as the order of the Letters in the bands.
1. The choice of the capital case of the second band, which determines that of the rest, is not entirely arbitrary. To regulate it 'tis necessary to have regard to the number of the ranks of the true square, which is the number 5 in the preceding example, and which is always the square root of the number, which expresses the multitude of the cases of the true square, and so I will call it the root of the square.
Take then a number at your own choice, provided nevertheless that it be less than the root of the square, and first to this very root, and that by adding two points, it be still first at the same root of the square: 'Twill be by this number that we shall determine the choice of the second capital case: and we call it the number determining.
The second capital case must not be the second case of the second band, because that this second case is found in the upright diameter of the augmented square, and that there must not be two Letters alike in any of the diameters of the augmented square: and so as the first capital case is already in the upright diameter, the second cannot be there. It is necessary on the contrary, that the case which you shall chuse in the second band, for the second capital, be as far distant from the second case of the upright diameter, as your determining number shall have Unites, and at the same time your second capital shall be removed from the first capital case as many transverses, as your determining number + 2 shall have Unites. Thus in the preceding example, the second capital case, viz. the case of the second band, where is the Letter d, is the second case after that, which is in the upright diameter, and it is in the fourth transverse underneath the first capital case, which alone is looked upon as a transverse, and the number 2, which determines this second capital case, is first to 5, which is the root of the square, and 2 + 2 that is to say 4, is likewise first to 5, the third case of the second band is therefore the first, which removes from the upright diameter, and it is with this that it is necessary to begin to compute the distance of the rest: so that the first case of this second band is in this sense the remotest of the second case, though to reckon after a contrary sense it touches it.
You may then in the preceding example, where the root of the square is 5, take either 1 or 2, or 4, which do give you three different cases, of which you may make your second capital case, 1 is first to 5, and 1 will give you the case wherein is b, three transverses distant from the first capital case. a is first to 5, and 2 + 2 that is to say 4, is also first to 5, and 2 will give you the case wherein is d, 4 transverses distant from the first capital case., 3 is also first to 5, but because that 3 + 2, that is to say 5, is not first to 5, 3 can give you in this example only a false capital case. 4 is first to 5, and 4 + 2 that is to say 6, is also first to 5, but from 6 it is necessary to deduct 5 which is the root, and there will remain 1. And 4 will give you the case wherein is e, the fourth in distance from the case of the diameter rising, and has a transverse near the first capital. The number 4 will give you then Bachet's disposition, who has placed all the capital cases in the first bar: and as often as for a determining number you shall take a less number by an Unite, than the root of the square, you will fall into Bachet's disposition.
3. From hence it follows, that the diameter ascending will not have any other capital case than the first, which it has already, and that so it will not have twice the Letter, which shall be in the capital cases. To prove it let us suppose that our bands be sufficiently extended towards the right, to make as many new uprights as we desire; and let us mark the first upright, which shall be as distant from the diameter ascending, as the root of the square has Unites: that is to say, which shall be the fifth on the right of the diameter ascending, if the root of the square is 5. And at a like distance from this first upright marked, let us mark a second, and then a third, and a fourth, always at an equal distance one from the other, until that there are as many uprights marked, as the determining number has Unites. In this case as the determining number and the root of the square are first amongst them, the last upright marked will be the sole one, whose distance to take it from the diameter ascending, would be divisible by the determinating number.
Suppose also, that now the bands are long enough, the capital cases are marked all together, and without ever returning to the first cases of the bands, as it was necessary to do, before that the bands were extended, because that then they had not cases enough after the capital, to receive all the Letters successively. I say that in these suppositions, none of these marked uprights will have a capital cases except the last: because that it is the sole marked upright, whose distance from the diameter ascending unto it, is divisible by the determining number: for as the uprights, wherein are the capital cases, are as removed (viz. the first from the upright, the second from the first, the third from the second, and so successively) as the determining number has Unites, it follow that no upright has a capital case when the distance from the upright diameter unto it, is not divisible by the determining number. 'Tis proved then that no marked upright, except the last, will have a capital case: and the capital case which is shall have will be the first beyond the number of the cases necessary to your augmented square, because that in counting the first capital case, there will be as many others before this, as the root of the square has Unites.
Now when you mark the capital cases in a square augmented, according to the method which I have given, so that when you arrive at the last case of a band, you return to its first case, as if it was after the last, you do no other thing, than successively to place all the capital cases, in respect of the diameter ascending, as in the case of the extension of the bands, you will place one after the other in regard of all the uprights successively marked. And none of your capital cases, except a first supernumerary, can fall into your ascending diameter, as no other, except a first supernumerary, could fall into your last upright marked.
4. But if you consider the first capital case, as a transverse, and that you make the same suppositions as before, so that there are as many transverses marked, as the determining number + 2 shall have Unites, and as distant (viz. the first from the first capital case, the second from the first, the third from the second, and so successively) as the root of the square shall have Unites: From this that the root of the square and the determining number + 2 are first amongst them, and from this that the determining number + 2 expresses the distance of the transverses, wherein will be the capital cases, you will prove that there shall be only the last transverse marked, which has a capital case, which will be the first supernumerary: and consequently, that the defective rank, the first capital case of which is the complement, will have no capital case, because that it is the first transverse marked: and you will prove also that the first supernumerary capital case must return to the transverse of the first capital case, and as it must return likewise to the upright diameter, it follows that the first supernumerary case, that is to say, that which you would mark after the last of the necessary, is the first capital case, because there is only this which is common to its transverse, and to the upright diameter.
5. From the order of the letters, alike in all the bands and alike also in all the bars, you will prove that all the letters alike, are at the same distance one from the other, and in the same order amongst them, as the letters of the capital cases amongst them, and that so all the cases which contain letters alike may be considered as capital, so that two letters alike, are never found in the same upright, nor in the same transverse, nor in a defective rank, nor in its complement. Which needs no other demonstration.
Demonstration.
This supposed, the demonstration of the Problem is easie, for whereas no letter is twice in any of the diameters of the augmented square, nor in any defective rank and its complement, it follows that every of the two diameters, and every defective rank and its complement, have all the letters, and that consequently they make the same sumum.