Freda Bedi Cont'd (#3)

[admin]

Part 1 of 2

The Saka Era of Varahamihira (Salivahana Saka) [Rep. from Journal of Indian History (Trivandrum), 36 (1958) 343-67, Excerpt, from Collected Papers on Jyotisha. P. 275-287
by T.S. Kuppanna Sastry (Former Hony. Professor, Sanskrit College, Madras)
1989

NOTICE: THIS WORK MAY BE PROTECTED BY COPYRIGHT

YOU ARE REQUIRED TO READ THE COPYRIGHT NOTICE AT THIS LINK BEFORE YOU READ THE FOLLOWING WORK, THAT IS AVAILABLE SOLELY FOR PRIVATE STUDY, SCHOLARSHIP OR RESEARCH PURSUANT TO 17 U.S.C. SECTION 107 AND 108. IN THE EVENT THAT THE LIBRARY DETERMINES THAT UNLAWFUL COPYING OF THIS WORK HAS OCCURRED, THE LIBRARY HAS THE RIGHT TO BLOCK THE I.P. ADDRESS AT WHICH THE UNLAWFUL COPYING APPEARED TO HAVE OCCURRED. THANK YOU FOR RESPECTING THE RIGHTS OF COPYRIGHT OWNERS.

-- Historical Dates From Puranic Sources, by Prof. Narayan Rao

The kaliyuga era was first attested to by the ancient astronomer Āryabhaṭa, who assumed the beginning of kaliyuga to be 3600 years before the 23rd year of his life, which corresponds to the year 499 CE. Traditionalists love referring to the inscription of King Pulakeśin II in Aihole, Karṇāṭaka, which allegedly supports this dating. However, this inscription dates from the year 634 CE and is therefore even younger than Āryabhaṭa. Moreover, some authors refer to a number of title deeds written on copper plates that allegedly go back to King Janamejaya, who is said to have lived near 3000 BCE. However, these “copper grants” are obvious forgeries that served the purpose to support claims of ownership. Hence the statement found in Āryabhaṭa’s work is in fact the oldest testimony for the kaliyuga era, and over a whole period of 3600 years, the alleged tradition did not leave any trace in literary or archaeological sources. It must therefore be considered speculation. While the Mahābhārata and the Purāṇas do provide evidence that planetary clusterings were observed and considered important in ancient times, there is no available evidence that could support the kaliyuga era commencing in either 3102 or 3104 BCE.

Serious scholars therefore, do not accept the idea that the kaliyuga beginning on 18th February 3102 BCE is based on a true, unbroken tradition. Rather they assume that this date was back-calculated by Indian astronomers of late antiquity. It served as a mooring point for a theory of planetary cycles, as given in the Sūryasiddhānta, the most important work on ancient Indian astronomy....

There is a text found in several of the Purāṇas that links the beginning of the Kaliyuga with the death of Kṛṣṇa. However, instead of a conjunction of all planets, it mentions a conjunction of the Seven Ṛṣis in the lunar mansion Maghā. This text can be found in several different variations in VP 4.24.102ff., BhP 12.2.24ff., BrAP 2.74.225ff., MatsyaP 271.38ff. The text begins as follows:

From the birth of Parīkṣit until the inauguration of Nanda,
one must know, there are 1015 (var. 1050, 1115, 1500) years.

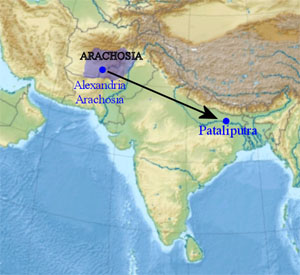
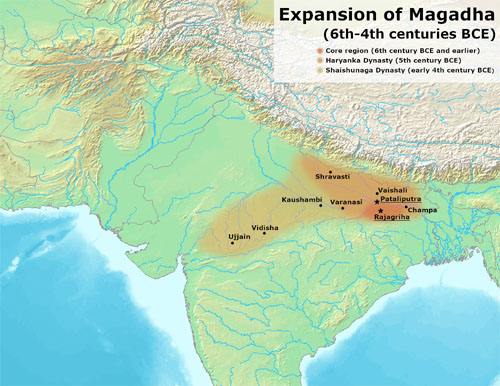
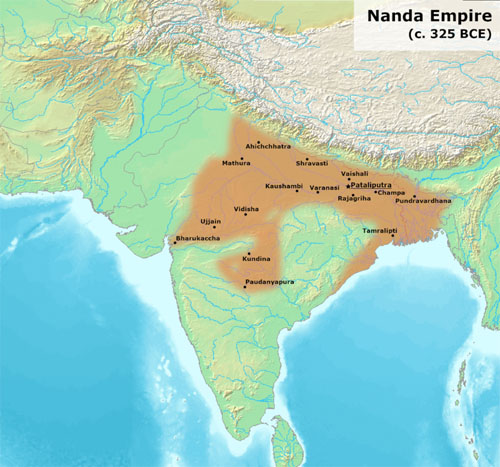
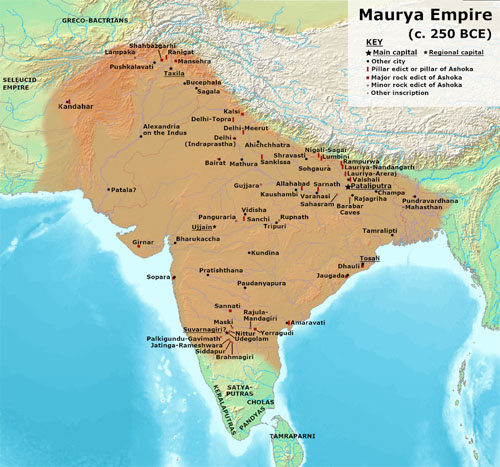
Parīkṣit is the first king of Hastināpura after Yudhiṣṭhira. His inauguration took place after Kṛṣṇa’s funeral, when Yudhiṣṭhira and his brothers renounced the kingdom and abdicated. Nanda is also called Mahāpadma in some versions of the text. He was the first king of the Nanda dynasty of Magadha. According to the Viṣṇupurāṇa, the Nandas ruled for about 100 years and were followed by Chandragupta Maurya, who seized power over Maghada in 321 BCE. The great number of variations of this text, e.g. the numbers of years mentioned, illustrates the text’s poor transmission. It is difficult to have confidence in any data given in it. Since the time between Parīkṣit’s seizure of power and Mahāpadma is between 1000 and 1500 years, Parīkṣit’s lifetime and the Mahābhārata battle would have fallen between the 20th and the 15th century BCE. This is in stark contrast to the traditional kaliyuga era, said to begin in 3102 BC. [However, traditionalists shun no effort in order to defend the Kaliyuga Era 3102 BCE. For that purpose, they are even ready to rewrite not only the whole history of India, but even the whole world history. The flowers of these absurd efforts: Buddha was allegedly born in 1887 BCE, Candragupta Maurya crowned in 1534 BCE, Aśoka in 1472 BCE, Śaṅkara was born in 509 BCE, etc. etc. (see K. Venkatachelam, The Plot in Indian Chronology, Appendix III). I shall not dwell on this, but refer to T. S. Kuppanna Sastry, Collected Papers on Jyotisha, p. 255-317, where the thinking errors in such approaches are exposed.]

-- Ancient Indian Astronomy in Vedic Texts, by R.N. Iyengar

The Saka Era of Varahamihira (Salivahana Saka) [Rep. from Journal of Indian History (Trivandrum), 36 (1958) 343-67.]

Introduction

With reference to chronology the word Saka is used in two senses: (1) As a common noun meaning any era (as for e.g., in the terms Yudhisthira Saka, Vikrama Saka, Malava Saka, Salivahana Saka etc.) and, (2) As a proper noun to mean a particular era called the Saka-kala or Saka Era. Most Indologists believe that the Saka Era is the same as what later is generally referred to as the Salivahana Saka which commenced with the month of Caitra occurring in 78 A.D., i.e., at the end of 3179 years of the Kali Era, for it can be shown that all astronomical works and commentaries thereon, wherever they mention a Saka Era, mean only the Salivahana Era, starting, as mentioned above, from 3179 Kali elapsed. But some like the late T.S. Narayana Sastri,1 [Cf. his Age of Sankara, (Madras, 1918), Pt. I, pp. 224ff.] Gulshan Rai,2 [Cf. his article, 'The Persian Emperor Cyrus, the Great, and the Saka Era,' Journal of the Panjab University Historical Society, (JPUHS), 1 (1932) 61-73, 122-36.] Kota Venkatachelam,3 [Cf. his Plot in Indian Chronology, (Vijayawada, 1953), 49-51; Indian Eras', Journal of the Andhra Historical Research Society, (JAHRS), 20 (1949-50), 43ff; 21 (1950-52), 61-73, 122-36.] and V. Thiruvenkatacharya4 [Cf. his 'Ayanamsa and Indian chronology: The Age of Varahamihira, Kalidasa etc.' Journal of Indian History (JIH) 28 (1950) 103ff. and 'The Andra Saka' JAHRS, 22 (1952-54) 161-8.] (VT) take the word to mean a certain Cyrus Era or Andhra Era which they say, started from 550 B.C.5 [In his Popular Astronomy, (Madras, 1958), pp. 135, 136, VT has changed to 551 B.C. without assigning reasons therefor.] Kane mentions two others of the group: Janannatha Rao, Age of Mahabara war (1931), C.V. Vaidya starting the Sakakala from Buddha's nirvana. We now find that T.S.N is the source for all these people, and almost every argument used by them is his. In his Age of Sankara he has used a Yudhisthira Era of 3140-39 B.C., and a Saka Era of 576 B.C., which he later shifted to 550 B.C. Still another view is expressed by K. Rangarajan, who takes it to mean an era which commenced from 523/22 B.C. with the first Viceroy of India appointed by the Persian Emperor.6 [Cf. Summary of his paper, 'On the Origin of Saka-kala, Proceddings of the Indian Historical Congress, Fifth Session, Hyderabad, 1941, p. 164.] They also try to show that it never means the Salivahana Saka.7 [In the case of Bhaskara II alone, VT concedes that the Saka Era mentioned by him is the Salivahana Saka.] What astounds us is that even where there is clear evidence that Salivahana Saka is to be taken, (in the shape of statements that 3179 is to be added to the years gone in the Saka Era to get the years gone in Kali)8 [E.G., Brahmagupta's Brahmasphuta-Siddhanta, Madhayamadhikara, I. 26; Bhaskara I's Mahabhaskariya, I. 4, and Laghubhaskariya, I. 4; Sripati's Siddhantasekhara, I. 25; Bhaskara II's Siddhantasiromani, Ganita., Madhyama., Kalamana., 28; Vatesvara Siddhanta, Madhyamadhikara, I. 10.] these scholars ignore it implicitly as in the case of the Saka-kala mentioned by Brahmagupta and Bhaskara II.9 [Cf. VT, Popular Astronomy, p. 137; Kota Venkatachelam, The Plot in Indian Chronology, Appendix, pp. xxx.] When this is the fate of such clear evidence, we need not be surprised if they identify with their alleged Cyrus or Andhra Era, the Saka Era mentioned in giving the epochs of karanas (astronomical manuals) as in the case of the Pancasiddhantika (PS), the Khandakhadyaka or the Laghumanasa, or in giving the date of a work given by the author, as for instance by Bhattotpala at the end of his commentary on the Brhajjataka or in inscriptions like the Aihole Inscription, or in sundry other places as in the Brhatsamhita 1.13, in all of which cases the identification has got to be made by examining the months and tithis and ksepas mentioned therewith.

The reason why they want to identify the Sakakala with the so-called Cyrus or Andhra Era is this: They believe that there was a “plot hatched by European Indologists” to post-date by several centuries the ancient events of Indian history, and that most Indian Indologists have become unconscious victims of that plot. They try to show that the Yudhisthira and Saptarsi Eras are everywhere identical, and were actually started 25 years after the beginning of the Kali Era. Using this they try to show that it is Samudra Gupta of the Gupta dynasty that is to be identified with the Sandracottus of the Greeks, and not Candragupta Maurya, which latter identification has been taken by the European Indologists as the sheet-anchor of Indian chronology, and the chronology of the dynasties before and after that time is established therefrom. Now, the identification of Sakakala with Salivahana Saka stands in their way. Hence their attempt to identify it with the so-called Cyrus or Andhra Era whose very existence is a matter of dispute, there being no evidence for it.

Most historians have not taken these people seriously, thinking that the very extravagance of their claims would be a deterrent to the acceptance of their views. But attempts have been made by Professors Gulshan Rai and VT to give astronomical and mathematical proofs to show that Varahamihira (VM) belongs to 123 B.C. and not to 505 A.D., (as he is generally believed to be), and thereby that the Sakakala mentioned by VM is the Cyrus or Andhra Era.10 [JPUHS I (1932) 124-27; and JIH 28 (1950) 103ff. and JAHRS 22 (1952-54) 172. Following his change to 551 B.C. as the Saka Epoch, in his Popular Astronomy, VT has changed VM to 124 B.C. from 123 B. C. But the arguments for the refutation of 123 B.C. are applicable in toto for the refutation of 124 B.C. also. ] They also attempt to show that the Sakakala mentioned by Bhattotpala as stated above is the Cyrus or Andhra Era, and therefore the Saka year 888 given by him corresponds to 338 or 339 A.D.;11 [JPUHS I (1932) 73 (date given 338 A D.), and JIH 28 (1950) 123 (date given 339 A D.) In his Popular Astronomy VT, has shifted this to 338 A.D. But in his ‘Andhra Saka’ VT gives this date as 340 A.D. (ib„ p, 173).] which would mean that Brahmagupta, Aryabhata Bhaskara I etc. must precede this date. The present article is intended to expose the hollowness of the above theory and to show that the astronomical arguments adduced in support of it (which to the lay reader may look formidable) are erroneous, and thus knock the bottom out of the claims of this set of writers.

Varahamihira uses the word Sakakala in a few places in his works.

(1) In the Brhatsamhita he says:

asan maghasu munayah sasati prthvum yudhisthire nrpatau ǀ
sad-dvika-panca- dvi-yutah Sakakalas tasya rajnas ca ǀǀ XIII. 3

“The Sapta-rsis were in the asterismal segment Magha when Yudhisthira was ruling over the earth. Any date by the Saka Era plus 2526 gives the time from that king, i.e., the date in the Yudhisthira Era."

(2) In his Pancasiddhantika (PS) the following occurs:

sapta-asvi-veda-sankhyam Sakakalam apasya caitra-sukladu ǀ

ardhastamite bhanau yavanapure somadivasadye. ǀǀ I. 8 ǀǀ 12 [Somadivasadye is the reading as emended by the late Dr. Thibaut and MM. Sudhakara Dvivedi in their edition of the PS. From the two manuscripts of the work available from the edition and from quotations elsewhere, four readings are known: saumya-divasadye, bhaumya-divasadyah, bhauma-divasadyah and bhauma-divasakhyah. On the propriety or correctness of these readings see below.]

“Deducting 427 of the Saka Era, (from the years in the Era) at the beginning of the light half of Caitra, which falls near sunset at Yavanapura, beginning a Monday...”

(3) Br. Sam. VIII 20-21. This will be discussed, later.

(4) In Pancasiddhantika, XII. 2. but it is not used by these scholars.

In (1), a synchronism is found between the Saka Era and the Yudhisthira Era. We shall not discuss this synchronism here but rest content with saying that whatever be the Sakakala mentioned in (2), it is highly probable that the same is mentioned by (1). In (2), it is clear, the epoch of the Pancasiddhantika is given as 427 Saka elapsed, which means the date of the work must be c. 427 Saka, and thus VM’s time can be fixed. If as VT and others say the Sakakala meant here is the Cyrus or Andhra Era of 550 B.C., then the date of VM must be 427 years after 550 B.C., i.e., 123 B.C., which Gulshan Rai and VT have tried to establish by their special arguments. If it is the same as the Salivahana Saka, then VM’s date must be 427 years after 78 A.D., i.e., 505 A.D.

Here we do not propose to go into the question whether there was a Saka Era beginning from 550 B.C. or whether it is necessary to postulate such an era in view of the reference in the Brhatsamhita Sloka quoted above which is discussed in the next paper ‘The untenability of the ‘postulated Saka era of 550 B.C.’ We shall confine ourselves to showing that the Sakakala of VM’s PS is the Salivahana Saka, and therefore 427 Saka (elapsed ) corresponds to 505 A.D. As we have stated before, we shall also show that the special arguments to the contrary advocated by Gulshan Rai and VT and their conclusion that VM’s date is 123 B.C. cannot stand.

Internal Evidence for Salivahana Saka

There is plenty of internal evidence to show that the date meant by VM is 505 A.D. and not 123 B.C. It consists of the many ksepas (i.e. values of the Mean longitudes etc. at Epoch) found in the work, and the names of certain authors which it mentions. We shall take the ksepas first.

In PS I.14, VM gives a Saura period of 1,80,000 years or revolutions of the Sun, in which there are 66,389 intercalary months and 10,45,095 suppressed tithis. From this we can get that there are in this period 2,406,389 revolutions of the Moon and 65,746,575 civil days. Comparing this with the Yuga-elements derivable from the Khandakhadyaka13 [Khandakhadyaka, (Tr. P. C. Sengupta. Calcutta, 1934), I. 3-5, 13, 14; II. 1-5.] of Brahmagupta (which follows the Ardharatrika system of Aryabhata and whose elements are identical with those of a Paulisa Siddhanta quoted by Bhattotpala in his commentary of the Brhat Samhita),14 [Cf. Brhat Samhita. Ed. Sudhakara Dvivedi, Banaras, 1895, Pt. I, pp. 28-30.]— not the Paulisa of the PS— we find that this is only a sub-yuga forming a twentyfourth part of the Yuga given by them, and this suggests that the Yuga- elements of the original Saura Siddhanta, of which the Saura of the PS is a compendium, are identical with those of the Khandakhadyaka etc. mentioned above; these elements, therefore, may also be called hereafter, the Saura elements. Now, all these systems have arrived at 0° Mean longitude for the Sun, Moon, Mars etc., 3 rasis for the Moon’s ucca (Apogee), and 6 rasis for Rahu’s head (Moon’s Ascending Node), at the beginning of Kali yuga, viz., midnight at Ujjain, Thursday/Friday, 17/18, February, 3102 B.C. Taking that Saka 427 mentioned in PS I. 8, refers to Salivahana Saka 427, (equivalent to 3606 Mean Solar years after the beginning of Kali), we have 1,317,123 days, 3 nadis 9 vinadis gone in Kali, and arrive at 3 nadis, 9 vinadis, after the midnight at Ujjain, Sunday/Monday, 20/21 March 505 A D.15 [3606 after Kali is not 504 A.D. as some people may think. As there is no zero year B.C. or A.D., we apparently arrive at a date one year later as the correct date. For errors of this kind see Kota Venkatachelam, JAHRS 21 (1950-52) 4, 7 etc.; Gulshan Rai, JPUHS, i. 73, 127.] The Saura of the PS takes this midnight as the Epoch for the computation of its Star-planets (Tara-grahas), viz. Mars etc. If we compute the Mean Mars etc. for this epoch, using the Saura elements, the results agree with the respective ksepas given in the PS to the second in the case of Jupiter and Saturn, within 4" in the case of Mars and Venus, and 7" in the case of Mercury. Even this small difference is due to VM having arrived at the ksepas using the shortcut given by him in the karana and the number of days gone in Kali as the Ahargana (days from epoch).16 [PS, ch, XVI. (Thibaut and Sudhakara Dvivedi’s Edn. Reprinted by Motilal Banarsi Dass, Lahore, 1930).] If we also do the same there is complete agreement in the case of Venus also, and the difference is reduced to 1" in the case of Mars. In the case of Mercury there is difference of a few seconds still, which may be due either to VM desiring to give its ksepa correct to the minute only, or to some defect in the manuscript reading which has omitted the seconds; and one of the manuscripts has actually a reading ‘vilipti’ here.17 [See under PS, XVI. 9, ‘davo vilipti'.] For the Mean Sun and Moon, and the Moon’s Ucca and Rahu, the epoch taken is the Midday at Ujjain just preceding the epoch of the Star-planets, i.e., the midday of Sunday.18 [PS, IX. 1.] Here too, checking the ksepas in the manner given for the Star-planets, we find perfect agreement in the case of the Sun and Moon, and agreement within 4" in the case of the Ucca. In the case Rahu the available manuscripts are so vitiated that Thibaut and Sudhakara Dvivedi (T-S) have failed to give the ksepa fully. Using the letters available in the manuscripts, the relevant verse may be read as:

trighanasataghne navakaikapaksaramendu- dahanasat-sahite ǀ
svarayamavasubhutarnavagunadhrti-bhakte kramad rahoh ǀǀ IX. 6 ǀǀ

The ksepa for Rahu enunciated in this verse as reconstructed above, agrees within 1" with its value according to the Khandakhadyaka elements.19 [S. B. Dikshit has arrived at the same result independently. See his article, ‘The Original Surya-Siddhanta’, Indian Antiquary (IA). 19 (1890) 49, 54.]

This perfect agreement is the reason why S. B. Dikshit has retained the date March 505 A.D. in spite of the difficulties he encountered in interpreting PS I. 8 with reference to the Saura.20 [Dikshit, Ib., 45-54.] For, no date, within many thousand years before or after 505 A.D. will agree with the ksepas in the manner shown above, not to speak of 123 B.C. When such is the case, VT quoting from Dikshit,21 [Ib. 46-47.] a passage, which to those that have not read Dikshit’s article in full will appear to involve an irremediable contradiction, says that 505 A.D. should be abandoned in favour of 123 B.C. on account of this. As the manner of VT’s quoting22 [JIH 28 (1950) 108.] from the article may create an impression in the readers’ minds which Dikshit did not intend, and as VT himself concludes from the quotation that the agreement in the ksepas discovered by Dikshit is null and void, and as he does not realise (as seen from his remarks under the quotation) that if he gives 123 B.C. for VM, he still has the responsibility to point out that the ksepas agree with his date, we intend making the discussion a little elaborate so that we may give Dikshit’s views in full with some pertinent observations on them.

The Saura Epoch occurs before the True Vaisakha Sukla Pratipad, ending on Tuesday. Dikshit wants to reconcile this with the statement in PS I. 8, caitrasukladau. He considers the point that according to Mean reckoning, it is ‘Adhika’-Caitra Sukla, but dismisses it, giving two objections: i. Why does not VM use the term ‘adhika-caitra-suklddau’? ii. Why should he take the Adhika-Caitra instead of the regular Caitra for the Epoch?23 [It will be shown below that there is absolutely no weight in either of these objections.] Dikshit concludes by saying that 'caitrasukladau’ might stand, because Amanta-Vaisakha-Sukla is Caitra-Sukla according to Purnimdnta reckoning. So there is no trouble at all for Dikshit as far as this goes. Therefore there is no need for VT to abandon 505 A.D., go to 123 B.C., and show that the Caitra Sukla Pratipad of this year occurs on a Wednesday, which weekday also is admissible according to one manuscript reading.24 [If it is 124 B.C., to which VT has shifted in his Popular Astronomy, the weekday is Thursday, and this is an additional argument against his date.] (Cf. the readings given above). It should be remembered that VT can score a point only if the weekday, viz., Wednesday of the Caitra Sukla Pratipad of 123 B.C. alone can effect the reconciliation, and not the Tuesday of the Caitra Sukla Pratipad of 505 A.D.

But really speaking, there is no need to reconcile the Saura with any part of PS I. 8, because it has reference only to the Romaka and the Paulisa. (If it can be applied to the Saura also, as indeed it can, it is good, but we have no right to demand it as Dikshit does.)25 [Ib. IA 19 (1890) 45ff.] PS I. 8-10 give the computation of Ahargana according to the Romaka; and I. 8 and 11 (and perhaps also 12 and 13) according to the Paulisa. I. 8 gives the Epoch, which is thus the same for both. The Epoch is the beginning of Caitra Sukla which ends 427 Saka, and the exact time is sunset at Yavanapura26 [VT has mistaken (JIH 28, p. 108; JAHRS 22, pp. 172) Yavanapura for Romakapura, and giving it a longitude of 90° west of Ujjain implies a desantara of 15 nadis instead of 7 nagis 20 vinadis which is specifically given as the desantara for it, in PS III. 13: Yavanantaraja nadyah sapta Avantyam tribhaga-samyuktah ǀ. For an explicit mention see PS, XV. 25: anyad Romaka-visayad desantaram anyad eva Yavanapurat | . Yavanapura would correspond to Alexandria as calculated front the desantara.] beginning Monday, i.e., 7 nadis, 20 vinadis after sunset at Ujjain. This is equivalent to 37 nadis 20 vinadis after Ujjain sunrise on Sunday, 20th March 505 A.D. The Ahargana with which to compute the Mean Sun etc. must be reckoned from this point for Romaka and the Paulina, and their ksepas are for this point. The expression caitra-Sukladau is an indication that the months gone are to be counted from Caitra in computing the Ahargana, and the words “beginning Monday” is a check for the Ahargana, Monday being stated to be the first day of the Ahargana. For, the Ahargana got by computation may be a day more or less than the correct one (a fact well known to astronomers) because the ‘varying’ True Tithi has got to be used in the formula; and checking by Monday beginning from the Epoch, viz., 0 Ahargana, it may happen that one day has got to be added or subtracted. This can be made clear by an example.

Problem: What is the Ahargana for Saturday beginning, next to the Epoch?

By counting we see we must get 5 days for Ahargana. Let us now compute it. By the Romaka or Paulisa (or even Saura) almanac, the tithi gone at Saturday beginning is Caitra Sukla Caturthi. Using it in the above formulae enunciated in PS I. 8-11, 4 is got as Ahargana. But counting from Monday, 4 will give only Friday beginning. So we must add 1, and give 5 as the correct Ahargana if it should agree with Saturday beginning. We see here the use of the check. This is the purpose for which the weekday beginning the Epoch is given, and it is not merely to satisfy the curiosity of the reader. From this we can see that ‘Monday’ is necessary, and ‘Tuesday’ or ‘Wednesday’ will be wrong. So in PS I. 8, ‘soma-divasadye' or ‘soma-divasadyah' must have been VM’s original reading. ‘ Bhauma' must have been a scribal error, or the correction of some revisor who did not understand what was necessary, but thought that the weekday of the True Suklapratipada gone must be given here, and this must have given rise to 'saumya’, a mixing of the two. Here T-S have rightly given the emendation ’soma-divasad e'. We may venture to give another suggestion, even if it may not appear very convincing to some. The emendation of T-S is not really essential and we can adopt the manuscript reading ‘saumya’ as such and take it in the yaugika (derivative) sense, meaning 'day pertaining to the Moon’, i.e. Monday. Though there is the dictum ‘Rudhir yogam apaharati' (‘the meaning obtained by usage is stronger than that got by derivation’), still at such an ancient period as VM’s, when the weekdays must have come into use very recently, the word Saumya-divasa might not have become rudha in budha-vara as it is now. Also when other things require the derivative sense, we are permitted to abandon the rudha sense.

The above discussion has been necessitated here by a desire to remove any doubt created in the readers’ minds by Dikshit’s dissatisfaction, which may be interpreted as going against the case for 505 A.D.27 [It is only dissatisfaction and nothing more, and it may be noted that Dikshit himself gives reasons for the adoption of 505 A.D. (Ib., p. 46). Also, Bhattotpala’s reading is [x]. We have since found in the editorial work with regard to the Pancasiddhantika that his readings are generally correct. We have also found during this work that PS I 17-20 gives Monday alone.]

We may now proceed to show that the ksepas of the Romaka and the Paulisa also as well as the adhimasa and avamasesa of their rules for ahargana, agree with 505 A.D. and not with 123 B.C. We have seen that the epoch for the Romaka and Paulisa is 37 nadis, 20 vinadis from sunrise at Ujjain on Sunday, 20 March 505 A.D. (It must be noted that Dikshit does not question this.) The Romaka Mean Sun at Epoch can be seen to be 359° 34-1/2' by taking the ahargana as zero in PS VIII. 1, and working with the ksepa left. This means that 26 nadis after Epoch, the Mean Solar month Mesa begins. In the same way we get the Mean Moon at Epoch from PS VIII. 4, to be 356° 12', using the emended reading 'krtastanavakhaika'; if the reading 'krtastanavakaika' found in the manuscript and followed by TS and Dikshit is used, it is 359° 19' at Epoch for TS, and 2° 24' for Dikshit who taken that the Moon is given for sunset at Ujjain. From this we see that the Mean New Moon according to our interpretation will take place at 16 nadis, 36 vinadis after Epoch, i.e., 9 nadis, 24 vinadis before the Mean Sun comes to Mesa. According to TS’s value for the Moon, it is 24 nadis, 42 vinadis before the Mean Sun at Mesa; and according to Dikshit, 32 nadis. It must be noted that according to all the three interpretations, the Mean New Moon just precedes the Mean Solar year, i.e., the New Moon end begins the Mean Caitra and is very near the Epoch.28 [It may be asked why only the Mean Caitra and the Mean Solar year are taken into consideration in this explanation. It is because the word Caitra is given in the context of the Ahargana rule, whose constants, multipliers and divisors depend upon the Mean Sun and Moon. If we use the True month and Tithi in the computation, it is because we have no other go and that is why there has to be the check by the weekday of the Epoch.] The corresponding ksepas of the Paulisa also will be found to give the same result. Thus the word Caitra in PS I. 8 presents no difficulty, as it is mentioned only in relation to the Romaka and the Paulisa. Also, the avama and the adhimasa sesas of the Romaka and the Paulisa found in PS I. 9-11, agree, within the limits of accuracy, with the time of the day when the respective New Moon occurs, and its distance from the beginning of the Mean Solar year as found from PS VIII and III. From the foregoing facts we see that the beginning of Caitra should fall very near the beginning of the Mean Solar year, which it does if we take 505 A.D. If 123 B.C. is taken, it is about 20 days away, and so there is disagreement with the ksepas of PS I. 8-11, and those of the Sun and the Moon in PS III, VIII and IX.

In the case of the Saura, an examination of the Sun’s and Moon’s ksepas given in PS IX. 1-2 will show that the Mean Solar year ends at 3 nadis, 9 vinadis after midnight, Sunday/Monday, 20/21 March, (as we have already shown), and the Mean New Moon falls about 12 nadis, 30 vinadis after the Mean Solar year. Thus there is a Mean Adhimasa following the Epoch of the Star planets, i.e., midnight, which can be called Caitra, as Dikshit himself has accepted.29 [The rule giving this is this: ravisankramanad urdhvam yo yo masah prapuryate candrah ǀ caitradih sa jneyah purtidvitve 'dhimaso ’ntyah ||] As it is very close to (i.e. only 12 nadis, 30 vinadis from) the beginning of the Mean Solar year, and as in computing the Ahargana the practice is to see whether an Adhimasa has taken place or not in the months gone used for reckoning, and adjust the number of adhimasas got by adding one or reducing the adhimasas by one, by treating a large adhimasa-sesa as unity or not counting one just got by computation, no harm will ensue if this Adhika-Caitra is treated as regular Caitra, taking the previous regular Caitra as Adhika-Phalguna. And there is the advantage of dispensing with a ksepa for months gone at Epoch. So even if PS I. 8 applies to the Saura as Dikshit thinks, the objection which he has to using the term ‘caitradau’ for this vanishes, and there is no need to explain it in the manner he has done.30 [Dikshit, Ib., p. 51.] Thus all the difficulties raised by Dikshit are answered, and not a trace of any objection for 505 A.D. is left.

[admin]

Part 2 of 2

We may now proceed to give another piece of evidence to show that the date cannot be 123 B.C. In PS XV we find the following sloka:

Lankardharatrasamaye dinapravrttim jagada caryabhatah //
bhuyas sa eva suryodayat praha Lankayam // 20 //

Here is a reference made by VM to Aryabhata and his two works, the well-known Aryabhatiya, and his less known work referred to by later authors as his Ardharatrika System, manuscripts of which are yet to be discovered, but whose nature is fully given by Bhaskara I (6th-7th cent.) in his Mahabhaskariya.31 [Mahabhaskariya, (Ed. T. S. Kuppanna Sastri, Madras, 1957), VII, 21-35. See the Editor’s Introduction to this edition, pp. xliv-vi.] In the Kalakriyapada of his Aryabhatiya, Aryabhata says:

sastyabdanam sastir yada vyatitas trayas ca yugapadah /
tryadhika vimsatir abdas tadeha mama janmano 'titah // 10 32 [There is a suggestion by some to emend sastih into sadbhih and take Aryabhata to 360 Kali ( e.g ., Kota Venkatachelam, The Plot in Indian Chronology, Ap. Ill, p. xxi). But with sadbhih the word ca in the verse becomes meaningless. It is T.S.N. that started this too. He says in his work that he has a copy with the reading sadbhih. (Knowing him, we have to doubt his veracity.) We can add some more arguments: (1) T.S.N.’s reading would mean that Aryabhata wrote c. 2741 B.C. Who will swallow this! What about the language. (2) Aryabhata’s first point, as of all other astronomers, is an insignificant position, is Asviui near a very faint star (V. Piscium). But the vernal equinox c. 2741 B.C. was at nearly 45° off, in Rohini. If his work was to be of any use in the matter of Ahas, Lagna, declination, shadow, solar eclipse, etc., he should have instructed an addition of about 45° to the longitude got by his work, or else these items would be got very very wrong. T.S.N. has not seen the self contradiction here, being a layman, and his trick has failed. Also manuscripts of the work give only sastih and all known ancient commentaries explain the verse only with sastih; Cf. Bhaskara I’s Arya bhatiyabhasya: sastyabdanam sastih, sastir abdah sastigunah ityarthah; Suryadeva Yajvan’s Aryabhataprakasa: satsatadhika-trisahasramitesu (3600) suryabdesu gatesu; Paramesvara’s Bhatadipika: satsatadhika-sahasratraya (3600) (Edn. Kern. Leiden, 1874, p. 58); Gargyakerala Nilakantha Somayaji’s Bhasya...sastyabdanam sasteh...kaler arabhya sagstyabdanam sastir gata...,idanim prakrtistham ayanam (TSS No. 101, pp. 12-13).]

This says that at 3600 Kali (expired) Aryabhata had completed twenty-three years of age, and 3600 Kali is 499 A.D. VM’s reference is certainly to this Aryabhata as can be gathered from the mention of him as the author of both the Ardharatrika and the Audayika systems. It follows, from this that VM must be later or at least a contemporary of this Aryabhata. So VM can belong to 505 A,D. and not to 123 B.C. Thus all internal evidence— and we have seen plenty of it—points to 505 A.D. as the time of VM.

The Ayanamsa argument examined

Now Profs. Rai and VT have advanced an argument based on Ayanamsa to show that VM must be as early as 123 B.C.33 [Rai, JPUHS I (1932) 124-27; VT, JIH 28 (1950) 104-06.] Being interspersed with mathematics, this argument may seem unassailable to some, unless its hollowness is exposed.

Being more full, we may discuss VT first. What VT says may be put succinctly as follows: (i) At the time of VM the Summer Solstice was at the end of the asterismal segment Punarvasu, (or what comes to the same thing, the Vernal Equinox had a longitude of 3° 20' reckoned from the zero point of the Ecliptic), as gathered from VM’s own statements in the PS and the Brhat Samhita. (ii) Taking the Ayanamsa (i.e. the total precession) to be zero at VM’s time, there is an Ayanamsa of 28° 15' in April 1909 A.D. (It comes to this: The Vernal Equinox has receded 28° 15' from the original position of 3° 20', and its position in 1909 is 335° 5' from the zero point of the Ecliptic), (iii) Using the correct rate of precession (ayana-calana ) per annum, 50".2585— nx0".000225, where n is the number of years before 1909, for a precession of 28° 15' to take place, n must be 2031 years, (iv) This means 2031 years before 1909, i.e. in 123 B.C., the Ayanamsa was zero, and therefore 123 B.C. is the date of PS.

We admit that if (i) and (ii) are correct, (iii) and (iv) follow automatically. But (i) and (ii) are not correct , as we shall show. Relating (i) there are the following three slokas of VM, which are quoted by VT also:34 [ Ib., p. 104.]

aslesardhad daksinam uttaram ayanam raver dhanisthadyam /
nunam kadacid asid yenoktam purvasastresu //
sampratam ayanam savituh karkatakadyam mrgaditas canyat /
uktabhavo vikrtih pratyaksapariksanair vyaktih //
Br. Sam, III. 1-2 //
aslesardhad asid yada nivrttih kilosnakiranasya /
yuktam ayanam tada ’sit, sampratam ayanam Punarvasutah // PS III. 21 //

‘‘Certainly at one time the turning of the Sun towards the south was from the middle of the Aslesa segment, and the turning north was from the beginning of the Dhanistha segment, because this is mentioned in ancient works.

“But now the turnings are from the beginning of the Karkataka and Makara rasi segments, respectively. If this does not happen (in future, on account of precession), the amount of deviation is to be determined by observation.” (Br. Sam. III. 1-2).

“When the Sun turned away south from the middle of Aslesa, it was proper for that time. But now the turning away is from Punarvasu.” (PS III. 21).

Now in the sloka from the PS, “from the middle of Aslesa” corresponds to the same phrase in the quotation from the Br. Sam. III. 1; and “from Punarvasu ” corresponds to "the beginning of Karkataka” in Br. Sam. III. 2 above, the same phenomenon of precession being described in both. So “from Punarvasu ” must be taken to mean a point three quarters from the beginning of the segment, for that is the point corresponding to the beginning of Karkataka. But VT who wants the end of Punarvasu to be the turning point, wants us to shut our eyes to the specific reference to the “beginning” of Karkataka, and take it to mean “somewhere” in Karkataka, giving the reason that the word is found in a mere Samhita and not in a karana like the PS. It seems he has not taken note of the many passages in the PS itself that specifies the ‘beginning’ of Karkataka as the point. For instance, in the sloka next but one, i.e., PS III. 23, we find “mesa-tulddau visuvad", “at the beginning of Mesa and Tula, are the Equinoxes”. One Sloka later we have again:

udagayanam makaradau rtavah sisiradayas ca saryavasat /
dvibhavanakalasamanam, daksinam ayanam ca karkatakat // PS III. 25 //

In XIII. 10, we have, “At the end of Mithuna the Sun revolves at an altitude of 24° at the N. Pole”.

Also VT says that Punarvasutah can mean only from the “end of Punarvasu”. This interpretation is wrong. It only means “from Punarvasu”, and can mean any point in it. Gramatah pattanam pratisthate does not only mean ‘he starts from the border of the village’. It can mean any point in the village.

Further, the context in which aslesardhat etc, is found, itself specifies a point If segments from the middle of Aslesa and this point is three quartets of Punarvasu. In the immediately preceding sloka, VM states that Vyatipata-punyakala occurs when Sun plus Moon equals 17 asterismal spaces, i.e., 17x13° 20', or 226° 40', as opposed to our expectation that it should occur at the middle of the 14th (i.e., at 180°) according to the definition given in the 3astras.35 [See for instance, Surya Siddhanta, XI. 1-2: ekayanagatau syatam suryacandramasau yada. |; tadyutau mandale krantyos tulyatve vaidhrtabhidhah || ; viparitayanagatau candrarkau krantiliptikak | ; samas tadvad vyatipato bhaganardhe tayor yutau ||] There is a difference of 46° 40' or 3-1/2 spaces that has to be explained. As Yoga is obtained from the combined longitudes of the Sun and the Moon, a change of 1-3/4 asterismal segments in the longitude of each, caused by the shifting of the origin of reference will explain the difference of the 3-1/2 spaces. This shifting of the origin, by the precession of the equinoxes, is mentioned in aslesardhat etc., and this must be If segments as required, and the point at f Punarvasu follows, for it is this point that is 1-3/4 segments behind the middle of Aslesa.36 [For a fuller discussion, see the writer’s Introduction to his edition of Mahabhaskariya, Madras, 1957, pp. xxv-xxxv. Further, since VT has not brought into the argument either the Caitra or the Dhanistha Paksa of the zero-point of the Ecliptic, we have avoided dragging them in and confusing the issue.]

Still another proof can be adduced to show that 3/4 Punarvasu is to be considered as the point in question. If it is the end of Punarvasu, the Vernal Equinox will be, as we have already stated, at +3° 20' from the zero point from which the longitudes of the Sun, the Moon etc. are reckoned. So, to get the declination of the Sun etc., to compute the daylight, the shadow and other things, in short, for all work usually given in the Triprasnadhikara of a siddhanta, we must be instructed to deduct 3° 20' from the longitudes got by computation, and use this for the calculation, as the longitudes from the Vernal Equinox are to be used here. In as much as such an instruction has not been given anywhere in the text, we must take it that the zero point and the Vernal Equinox were coincident, which means that the Summer Solstice was at 3/4 Punarvasu. Now in (ii), VT has budgetted for an Ayanamsa of 28° 15'. But the above fact will result in a cut of 3° 20', and VM will be lifted 240 years from the intended 123 B.C. towards the true place, 505 A.D.

Now we may pass on to consider (ii), viz., VT’s statement that in April 1909 A.D. there is an Ayanamsa of 28° 15', taking it to be zero at VM’s time, when according to VT the Vernal Equinox was +3° 20' from the zero point, i.e. there is a total ayanacalana of 28° 15', from VM’s time to 1909 A.D. VT makes up the 28° 15' necessary for him, by piecing together four different quantities: (a) the distance between the Vernal Equinox and the zero point, both referring to VM’s time, equal to 3° 20'; (b) the late L. D. Swamikannu Pillai’s (LDS) calculation of the Ayanamsa in 1909 to be 22° 25' which is the equivalent in degrees of the time from the Sun at the Vernal Equinox of 1909 to its entering the Sign Mesa in the same year according to Surya Siddhanta; (c) what VT calls a Bija (i.e. correction) of 218 days, equivalent to 2° 9'; and (d) an error of observation equal to 16'. Of these four quantities, we have already seen that VT cannot have (a), by the fact that the Summer Solstice was at 3/4 Punarvasu and not at the end of Punarvasu in VM’s time. So 3° 20' is cut off from the 28° 15'. We shall not discuss (d), for we except to point out below what mischief even this can do. That leaves us (b) and (c) to deal with.

We shall take (b) first. VT uses the Ayanamsa 22° 25' calculated by LDS in a manner not intended by him. To understand how it is so, it is necessary to make clear the principle involved in the calculation.37 [See LDS, An Indian Ephemeris. Madras, 1922, Vol. I, Pt. i, pp, 457-58: “Appendix (ii) Luni-Solar Precession as applied to Indian Astronomy—The year of Sunya-ayanamsa, A.D, 533, how determined".] LDS found from the Nautical Almanac that at 02143-day on the 21st March 1909, the True Sun was at the Vernal Equinox. He found that according to the Surya Siddhanta (Modern, not the Saura of PS), the True Sun reached the First Point of Mesa at 09492 day on 12th April 1909. From the difference between the two moments, equal to 227349 days, using the rate of motion of the sun at that interval, he calculated the Ayanamsa to be 22° 25'. Suppose LDS had used the time of the True Sun at Mesa (Mesa Sankramana as it is called) of some other Almanac like the Drk Almanac or Vakya Almanac, he would have got different Ayanamsas, for it is a well-known fact that Almanacs vary in their times of Sankramana. Which ayannamsa are we to adopt? Which is the ‘correct’, Ayanamsa? By ‘correct’ Ayanamsa is meant the total precession in degrees, of the Vernal Equinox, from a specific point on the Ecliptic, which we call the zero point, during the interval 1909 and the time when we take the Vernal Equinox to coincide with the zero point, in our case the time of VM. According to this criterion none of the present-day Almanacs gives the ‘correct’ Ayanamsa. The following is the reason: If the length of the year adopted by an almanac is the correct Sidereal year, viz., 365 days 15 nadis, 229 vinadis, so that at the end of every year the Sun returns to the specified zero point, then this way of finding the Ayanamsa will yield the ‘correct’ Ayanamsa. But the old system Indian Almanacs use, instead of the above correct Sidereal year, the Sidereal year of the Aryabhatiya (365-15-31-15, adopted by the Vakya Almanacs), or of the new Surya Siddhanta (365-15-31-31, adopted generally by LDS in his Ephemeris) and the like, which though called Sidereal, are very nearly Anomalistic, being about 8-5 or 8-6 vinadis longer than the correct Sidereal year. As a result, the First Point of Mesa moves forward leaving the zero point behind at the rate of 8'5" per annum. So if we adopt LDS’s method of using the time of the True Sun at the First Point of Mesa according to a particular Almanac to get the Ayanamsa, we must deduct from the gross Ayanamsa got, the accumulated interval between the zero point and the First Point of Mesa of that Almanac, to get the correct Ayanamsa. (This accumulated interval may be called the ‘Procession’ of the First Point of Mesa for that Almanac). It is this correct Ayanamsa that should be divided' by the correct rate of precession of 50" 2585 etc. to get the year when the Vernal Equinox was at the zero point. If, on the other hand, we use the gross Ayanamia got by LDS’s method, we should divide it by the gross rate of precession (which is the correct rate of precession ‘plus' about 8 5"), to get the year, for the gross Ayanamia increases not by the correct rate of precession but by the gross rate of precession, viz. 50" '2585 etc. etc. increased by about 8'5". This is the reason why most Indian systems give nearly V as the rate of precession. The reader will find our statement corroborated by sections 64 and 277 of LDS’s Indian Chronology (Madras, 1911).

This is the reason why LDS divided his gross Ayanamsa by 58"78 and got 536 A.D. for VM as a first approximation.37a [Using this date LDS gets 533 A.D. as the correct date.] The gross rate of precession 58" 78 is got from the rate of procession (viz. 8" 52) plus the rate of correct precession 50" 26, for it is at this combined rate of 58" 78 that the Vernal Equinox recedes with reference to the First Point of Mesa, per annum. From this we see that it is wrong to use for this purpose the actual rate of precession given, even by the system, if any, as for eg. 54" per annum In the case of the new Surya Siddhanta or 1' per annum in the case of certain other Siddhantas, and so on; for these Siddhantas have found the rates of precession by actual observation of the Sun at the Vernal Equinox, and there is likely to be an error in the observation. According to the error the rates may vary. The nearer their rates are to 58"78, the better are their observations.

It is incumbent on our part, in the present context, to answer certain remarks made by VT on the above procedure of LDS. VT remarks:38 [His article, JIH 28 ( 950) 105.] “There are the following drawbacks in the whole argument (of LDS):

"(a) It was considered that Dakshinayana began when the Sun reached the beginning of Karkataka instead of the end of Punarvasu.

“(b) The fact that the modern tropical year goes on decreasing at the rate of 0'53 seconds per century was not taken into consideration.

“(c) At least at the time of Varahamihira, the Indian Siderial year—so designated at present—was really a tropical year and the value for the precession of the equinoxes must be taken as 50" 2585 —n X 000225" and not as 54"7505 as assumed by Swamikannu Pillai.”

Of these (a) has already been answered. As for (b), in the 14 centuries considered by LDS, the time neglected, by him is about 56 seconds, equivalent in 2" of the Sun’s motion. Is this not negligible in the context? As for (c), this is against the internal evidence of the PS. Excepting Vasistha38a [Vasistha’s is 365-15-0, midway.] and the Romaka, all the other Siddhantas in it give Sidereal years. The Paulisa gives 365 days, 15 nadikas, and 30 vinadikas, the Saura, 365-15-31-30, and the Paitamaha 366 days. By what stretch of imagination can these be called Tropical years, these years that are SO far greater than the correct Sidereal year that they border on the Anomalistic? As for LDS not taking 50" 2585 for division, we have answered it by saying that this would be proper only if the correct Sidereal year, 365-15-22‘9. had been used throughout the period of which we are considering the Ayanamsa. Secondly, where has LDS assumed a rate of precession of 54"7505, and in which context?

It should not be thought that because the modern Drk Almanacs use the correct Sidereal year equal to 365-15-22.9, the time of the True Sun at their First point of Mesa will give the correct ayanamsa. These almanacs were started recently and they arbitrarily fixed for themselves such ayanamsas as would keep their sankramanas within reasonable distance from those of the old almanacs. The very fact that the sankramanas vary only within a matter of nadis, shows this, for considering the difference between the correct Sidereal year and the so- called Sidereal years of our siddhantas, even within a period of 420 years there will be a difference of one day, and for the period we are considering, viz. 1400 years or more, there should be a difference of more than three days, the Drk Sankramanas occurring earlier. To avoid the hue and cry that would be raised if the sankramanas in their almanacs are found to occur thus, more than three days earlier, the Drk Almanac makers fixed for themselves ayanamsas that would keep their sankramanas near enough to those of the old system almanacs.39 [In 1925 the Almanac makers met in Conference at Poona and adopted an ayanamsa of 22° 40' 39' for 1925 proposed by R. N. Apte, M.A., Professor of Mathematics, Rajaram College, Kolhapur, arrived at by taking the True Sun's position at Mesa-sankramana in that year according to the Surya Siddhanta as the zero point. On this see C. G. Rajan Raja Jyotisa Gapitam, (Madras, 1933), Section— Conversion of Heliocentric etc., ch. VI, p. 56.] The Caitra or the Dhanistha paksa has come in handy for them to fix their ayanamsa in this manner, but these paksas are contradictory to all schools of traditional astronomy which have adopted the Raivata-paksa alone.40 [C. G. Rajan gives the actual ayanamsa according to the Raivatapaksa to be 18° 56''45".7 in 1925; see Ib„ p. 58.]

To continue the main argument. As, in the manner already stated, the number of years got to be deducted from 1909 to find the Zero Point should be the same, whether we divide the gross ayanamsa by the gross rate of precession, or the correct ayanamsa by the correct rate of precession, and as the rates are in the ratio 7:6 approximately, the gross ayanamsa found by LDS (by using the time of sankramana of the new Surya Siddhanta) should be reduced by one seventh of itself to get the equivalent correct ayanamsa, which we find to be 19° 12'. So VT can have only 19° 12' and not 22° 23' by (b).

Now, we pass on to (c). (This is VT’s special.) What VT says amounts to this: Kali began at midnight 17/18, February 3102 B.C. But most Ephimerides give 0.579 days after sunrise on 15th February as the Epoch of Kaliyuga. So there is a difference of 2.18 (72.17) days which must be a bija correction. So we must add 2.18 days to the time of the True Sun reaching the First Point of Mesa in (b), viz. 0.9492 on 12th April. Thus the interval in days is increased by 2.18 days; which means 2° 9' more in ayanamsa, which will make up the 28° 15' required.

Now, what VT thinks to be a bija is really the interval between the times of the True and the Mean Suns reaching the First Point of Mesa. According to Indian astronomy the Sun’s Equation of the Centre is about 2° 9' at the time of Mesa Sankramana. So the True Sun is in advance of the Mean Sun by 2° 9' and reaches the First Point of Mesa earlier by about 2.18 days. As the Apogee of the Sun has an extremely slow motion according to Hindu astronomy, the 2 18 days practically continue through the ages to be the same. In (b), LDS took for calculation the interval between the True Sun at the Vernal Equinox and the True Sun at the First Point of Mesa which is quite proper. If he had taken the interval between the times of the Mean Sun at Vernal Equinox and the True Sun at the First Point, then indeed we shall be justified in adding 2.18 days; for then the interval first got would have been less by 2.18 days, on account of the Mean Sun reaching the Vernal Equinox later by 2.18 days than the True Sun. If we add 2.18 days, as we ought to now, we get the same interval of 22.735 days. Thus VT cannot have (c).

The error of observation, (d), is possible and may be allowed if required; but it must be remembered that it is arbitrary, indefinite and may be plus or minus. VT has taken (d) as error of observation, not from apriori considerations, but aposteriori, because this alone will give him, when added to the other quantities and divided by 50" 2585 etc., 2031 years to be deducted from 1909 and get 123 B.C. So the reader is warned against getting predisposed in favour of 123 B.C., simply because 1909 A.D. minus 2031 is exactly equal to 123 B.C., for this particular amount of error of observation has been arbitrarily presumed to get this very result.

In conclusion, we find that in VT’s ayanamsa of 28° 15', (a) is cut off, (c) is cut off, (d) may be ignored, and (b) is reduced to about 19° 12'. If we divide this by the correct rate of precession, 50".2585 etc., we get c. 534 A.D. as VM’s time. It may be noted how far away this is from 123 B.C., and how near it is to 505 A.D. (epoch).

The ayanamsa argument of Prof. Rai ( JPUHS I.124-27) is the saw as VT’s (a) and (b), with the difference that he takes (b) for 1931 instead of 1909. This amounts to 26° 3' 40" according to him, and committing the same mistake as VT of dividing this gross ayanamsa by the actual rate of precession, he says VM lived 1866 years before 1931, i.e., in 65 A.D. Since this does not take him to the desired 123 B.C. Prof. Rai thinks that this discrepancy may be overcome by assuming an appropriate error of observation, which in this case has to be as large as 3 degrees or so!

With showing that 427 Saka of VM is 505 A.D. and that the ayanamsa argument is fallacious, the main object of this paper is over. It is unnecessary to discuss the slokas from Jyotirvidabharana quoted by these scholars enumerating the nine gems of Vikramaditya’s court (dhanvantari-ksapanaka etc.) and the year given therein; for in the light of the foregoing discussion these must be taken as part of a romance, or an attempt at imposture by the author of the work.49a [For the unreliability of this work, see below, Sn. V of the paper on ‘The untenability of the postulated Saka era of 550 B.C.’] Nobody will take seriously this sloka jumbling men of different ages together, as no one will take seriously the other romance, the Bhoja Prabandha, for matters of history.

The Date of Bhattotpala

Both Rai and VT seek additional evidence for VM’s earlier date by making his commentator Bhattotpala himself earlier than 505 A.D.41 [Rai, JPUHS I (1932) 73; VT, JW 28 (1950) 103, JAHRS 22 (1952-54) 173.] We shall examine this now. Bhattotpala says at the end of his commentary on VM’s Brhajjataka that he finished writing it in Saka 888 (elapsed) on Caitra Sukla Pancami, which was a Thursday:

caitramasasya pancamyam sitayam guruvasare /
vasvastastamite sake krteyam vivrtir maya //

Here VT says that “the weekday does not come out correctly if we take either the Salivahana Saka or the Vikrama Saka. So the Saka mentioned by ... Bhattotpala refers only to the Saka with 550 B.C. as epoch”.42 [JIH 28 (1950) 109.] This means that if Bhattotpala’s Saka is taken as given in the Saka of 550 B.C., the weekday agrees; and so the date referred to is 888 years after 550 B.C., i.e., 339 A.D., (but in his ‘Andhra Saka’ he gives 340 A.D., cf. fn. 11 above) and so VM must be earlier still. But we have made the calculations, and we find that it is 339 A.D. that does not give the agreement; in that year the Caitra Pancami falls on Friday, ending at about 35 nadis. In his Popular Astronomy, pp. 136-37, VT has changed the date of Bhattotpala to 338 A.D., in accordance with his changing the Saka Epoch to 551 B.C. Strangely enough, here too VT asserts that he finds agreement with the weekday, viz. Thursda. 42a [It is an obvious fact that for a particular Tithi in a particular month the weekday cannot be the same in two consecutive years.] My calculation here gives Sunday, i.e. three days off, on this date. On the other hand there is perfect agreement with Salivahana Saka 888 (corresponding to 966 A.D.) if Caitra is in the Purnimanta reckoning which was prevalent in Bhattotpala’s time43 [In certain editions of Bhattotpala’s commentary on the Brhajjataka we find instead of the sloka quoted above, another saying that he finished the commentary on a Thursday in S'aka 888 on Phalguna-krsna-dvitiya. This too gives agreement with the weekday only if 888 is in Salivahana S'aka. If in the S'aka starting from 551 or 550 B.C. alleged, there is disagreement.] and place. If Saka 888 is elapsed year, Caitrasuddha- pancami falls on Thursday, at 25 nadis, February 28, 966 A.D. So we get the time of Bhattotpala’s finishing the work correctly as we expressed. Because we took the current Saka instead of the elapsed (elapsed is the more usual practice of the Hindus), we had recourse Purnimanta  reckoning, where too it is the previous Phalguna that agrees.

And there is also positive evidence to show that Bhattotpala has meant only the Salivahana Saka. He has commented on the Khandakhadyaka of Brahmagupta, who says that it is a representation of the (Ardharatrika ) system of Aryabhata.44 [See Khandakhadyaka, I. 1.] This means that Brahmagupta is later than Aryabhata (3600 Kali, corresponding to 499 A.D.) and that Bhattotpala must be later still. It is not possible to drag down, as VT and others do, both Aryabhata and Brahmagupta together into the earlier centuries, for the following reasons: The date of Aryabhata is definitely 3600 Kali, as already shown. Brahmagupta gives 587 Sakakala as the epoch of his Khandakhadyaka (I. 3). Brahmagupta elsewhere states that 3179 is to be added to the Saka year to get the corresponding Kali year (Cf. Brahmasphutasiddhanta, I. 26). Amaraja commenting on the above verse of Khandakhadyaka (1. 3) gives the Kali year corresponding to the epoch of the work (Saka 587) to be 3766 by adding 3179 to 587; and also calculates and verifies the ksepas and the weekday of the epoch taking the Kali year 3766, which is A.D. 665,45 [So VT’s statement in his Popular Astronomy, p. 137, that only 36 A.D., which date he gives for Brahmagupta, would agree with the weekday and not any other date, is wrong.] which therefore must be the time of Brahmagupta. Further, Brahmagupta is linked to Bhaskara II (who VT at least admits wrote his Siddhanta- siromani in 1150 A.D.) by an observed ayanamsa of about 11°. Bhaskara II also says that in Brahmagupta’s time the ayanamsa was so little that it was “unobservable even to that expert astronomer”.46 [Cf. his Vasana-Bhasya on his Siddhantasiromani, under Goladhyaya, Golabandhadhikara, 17-19.] So Brahmagupta cannot be dragged too far away from Bhaskara, and this condition will be fulfilled only if his epoch is in the Salivahana Saka. (TSN says in this connection that Brahmagupta, whom Bhaskara II eulogises as his learned ancient teacher, could not detect an observational error of 5'!!) And so his commentator, Utpala’s date, Saka 888, has also to be in the Salivahana Saka.

Prof. Rai advances another argument,47 [ JPUHS I (1932) 123-24.] which is his own and not given by anybody else. It is this: Brhat Samhita, VIII. 20-21, gives a rule from which, by using the Saka year, the corresponding Jovian year in the 60 year cycle Prabhava etc., can be got. He works it out for 1932 using the Saka starting from 550 B.C., and gets 52 years gone in the Prabhava series. Using the years gone in the Salivahana Saka of 78 A.D., he gets the 18th year in the series, viz. Tarana. He finds this Tarana given in North Indian almanacs. But he says this proves nothing beyond showing that the North Indian almanac- makers have adopted the Salivahana Saka for this rule. But the point at issue is which is the correct Saka to take. This can be found by working out the year from the Kali years gone till 1932, and seeing which of the two (52 or 18) it agrees with. Prof. Rai works out the Jovian years gone from the beginning of Kali, using the elements of the Surya Siddhanta,48 [The Surya Siddhanta, which Prof. Rai uses, wants actually the years from ‘Creation’ ( i.e. a point 17,064,000 years from the beginning of the Kalpa) to be used for this. But as a whole number of 60 year cycles have gone at the beginning of Kali, no harm will ensue if the Kali year is used as he does.] and dividing the result by 60 gets the remainder 52. Lo! this is the same as the remainder got by using the Saka of 550 B.C. So, that is the Saka intended by VM in his Brhat Samhita, he says. The argument seems to be perfect.

But this is the fallacy in it: If the Jovian year is to be worked out a priori using the Kali years gone, the years should be counted from Vijaya and not from Prabhava. This condition is specified in the very Surya Siddhanta whose elements Prof. Rai uses for computation, and this has been missed by him.49 [Cf. Dvadasaghna gurar yata bhagana vartamanakaih I ; rasibhih sahitah, suddhah sastya syur ‘'Vijayadayah‘' ǀǀ I.55 ǀǀ] Now counting 52 from Vijaya, we get only the 18th year of the Prabhava series, viz. Parana, and this agrees with Saka of 78 A.D. and not the Saka of 550 B.C. Thus Prof. Rai’s argument fails. In the result, it is only a proof for taking VM’s Sakakala to be the Salivahana Saka, and discarding the Saka of 550 B.C.

Prof. Rai seeks further support to his theory by stating (ib., p. 71) that, “Albiruni writing in 1030 A.D. not only talks of Bhaskaracharya, but also mentions his book ‘Karana Kutuhala’”, that the date of composition of Karanakutuhala given in the work itself, viz. Saka 1105, if taken in the Salivahana Saka would be 1183 A.D., i.e. 150 years after Albiruni, which is patently impossible, that “Weber in his Book on Sanskrit Literature (p. 262) notices this anomaly, but is unable to offer any explanation” (Weber, History of Indian Literature, English Translation, London, 1914), and that “if we take this Saka commencing from 550 B.C., the riddle is solved”, for this would take Bhaskara to the 6th cent. A.D., long prior to Albiruni.

The answer to Prof. Rai is given by Bhaskara himself who indicates that he uses only the Salivahana Saka, for he says that 3179 is to be added to the Saka year to get the Kali years gone (Cf. Siddh. Siromani, Ganita, Madhyama, Kalamana, 28). Moreover Albiruni’s words in the context do not warrant the name Bhaskara at all, nor does he mention anywhere a work Karana-'Kutuhala’ (the work named being a Karana-'Sara’). It has also to be added that Prof. Rai is not speaking the facts when he says that Weber “is unable to offer any explanation”. As a matter of fact, in contradiction to what Prof. Rai says, Weber offers on the very page that Rai refers to (page 262) several explanations: Weber says that “we have scarcely any alternative save to separate Albiruni’s ‘Bashkar’ son of 'Mahdeb' , and the author of ‘Karana- sara' from the Bhaskara, son of Mahadeva, and author of Karanakutuhala”. (Note that none of the three names, neither that of the author, nor of his father, which is really Mahesvara and which Weber himself draws attention to in a footnote, nor of the work, tallies). Weber again suggests that his translation of the Arabic words of Albiruni might be wrong, for “Albiruni usually represents the Indian bh by b-h, and for the most part faithfully preserves the length of the vowels, neither of these is here done in the case of Bashkar, where, moreover, the s is changed into sh”, and adds in a footnote that in the passage under discussion “there lurks not a Bhaskara at all, but perhaps a Pushkara”.50 [Weber’s doubts about the translation of the Arabic passage are only too well founded, for we find Sachau translating the passage as: “Further there is an astronomical handbook...by Vittesvara, the son of Bhadatta (? Mihdatta) of the city of Nagarapura, called Karanasara.” Cf. Alberuni’s India, E. C. Sachau, London, 1910, vol. I, p. 156. The [x] since published by the Astronomical and Sanskrit Research Society, New Delhi, gives "[x]" ([x], [x] I.1). [x] I.21 gives the date of work as 826 [x] and the author's birth as 802 [x] I. 10 gives that 3179 years are to be added to the Saka years to get Kali years.] Even if the passage refers to a Bhaskara, Weber suggests that "we may have to think of that elder Bhaskara, ‘who was at the head of the commentators of Aryabhata, and is repeatedly cited by Prthudakasvamin, who was himself anterior to the author of the Siromani”. It is in the face of these facts that Prof. Rai coolly asserts that Weber “is unable to offer any explanation!” (Here Rai only follows T.S.N’s remarks.)

We may add here that the epoch of Karanasara, which is mistaken for Karanakutuhala, is given by Albiruni as Saka 821 (A.D. 899) (Alberuni's India, Sachau, I. 392), and obviously Prof. Rai’s Bhaskara of the 6th cent, cannot write a work 300 years later! So Prof. Rai’s argument only goes against his own theory.

Thus nothing can shake the evidence showing that the Saka mentioned by VM is the Salivahana Saka and that the date Saka 427 given by him in his PS is 505 A.D. Incidentally it has also been shown that the Saka era used by Brahmagupta, Bhattotpala and Bhaskara II is the Salivahana Saka of 78 A.D.

We propose to show in a subsequent article the untenability of certain other claims of these scholars referred to in the Introduction and that everywhere when the word Saka occurs as the name of an era, it is only the Salivahana Saka that is meant, and therefore or otherwise there is no case for postulating a Cyrus or Andhra Era of 550 B.C.

[admin]

The Untenability of the Postulated Saka of 550 B.C. [Rep. from JIH (Trivandrum), 37 (1959) 201-24.], Excerpt, from Collected Papers on Jyotisha. P. 288-317
by T.S. Kuppanna Sastry (Former Hony. Professor, Sanskrit College, Madras)
1989

NOTICE: THIS WORK MAY BE PROTECTED BY COPYRIGHT

YOU ARE REQUIRED TO READ THE COPYRIGHT NOTICE AT THIS LINK BEFORE YOU READ THE FOLLOWING WORK, THAT IS AVAILABLE SOLELY FOR PRIVATE STUDY, SCHOLARSHIP OR RESEARCH PURSUANT TO 17 U.S.C. SECTION 107 AND 108. IN THE EVENT THAT THE LIBRARY DETERMINES THAT UNLAWFUL COPYING OF THIS WORK HAS OCCURRED, THE LIBRARY HAS THE RIGHT TO BLOCK THE I.P. ADDRESS AT WHICH THE UNLAWFUL COPYING APPEARED TO HAVE OCCURRED. THANK YOU FOR RESPECTING THE RIGHTS OF COPYRIGHT OWNERS.

THE UNTENABILITY OF THE POSTULATED SAKA OF 550 B.C. [Rep. from JIH (Trivandrum), 37 (1959) 201-24.]

I. Introduction

It has been shown in the preceding study that the Saka Era used or alluded to by astronomers like Varahamihira (VM), Brahmagupta, Bhattotpala, Sripati, Bhaskaras I and II, etc. is the era starting from 78 A.D., later known as the Salivahana Saka, and not the era of 550 B.C. postulated by the late T. S. Narayana Sastri (TSN) or V. Thiruvenkatacharya (VT) and called by them the Cyrus Era or the Andhra Era, respectively. Incidentally we have shown to be untenable their statements that Aryabhata belonged near to 2742 B.C., VM to 123 B.C., Brahmagupta to 36 A.D., Bhattotpala to 339 A.D. and Bhaskara II to 522 A.D., and thereby we have proved that VM belongs to 505 A.D. and Bhattotpala to 966 A.D. and indicated that the real date of Arayabhata is 499 A.D. and of Brahmagupta 654 A.D.1 [In the same way we can easily see that the date of Bhaskara II's work, the Siddhanta Siromani, is 1150 A.D., from his statement: rasa-gupa-purya-mahi (1036) sama S'aka-nrpa-samaye ’bhavan mamotpattih / ; rasa-guna (36) varsena maya Siddhanta Siromani racitah //]

In the same way it can be shown that wherever other astronomers or writers like Kalhana and Albiruni mention a Saka Era, it is this Saka of 78 A.D. they mean. The tradition of almanac-makers also supports this, for they all give in their almanacs only this Saka Era and not the alleged other one. In inscriptions and documents also, in short, in every case where a date in Saka Era is given, it is this Saka alone, though this is disputed by TSN and (till recently) by Sri Kota Venkatachelam (KV) in the case of the Aihole Inscription (to which we shall revert later).

II. VM’s Brhat-Samhita XIII. 3 considered

We shall now take up for discussion Brhat-Samhita of VM (Br. Sam.) XIII. 3 referred to by us in the previous paper, which TSN and others consider as their stronghold, and which we left over for detailed consideration later:

asan maghasu munayah sasati prthvim yudhisthire nrpatau /
sad-dvika-panca-dvi-yutah Sakakalas tasya rajnas ca //

This stanza occurs in the context of the Saptarsi-cara or the alleged ‘Motion of the Seven Sages’, (i.e., the group of stars Ursa Major or the Great Bear), among the twenty- seven asterisms, given for use in astrological prediction. To find the position of the group at any time, three things are necessary: (i) its position at a given time; (ii) the time elapsed from the given time to the time for which the position is required, and (iii) its rate of motion. The above stanza gives (i) and (ii), viz., that at the time of Yudhisthira’s rule the Sages were at the asterismal segment Magha, and the time elapsed from this time to any year in the Saka Era is the number of the year in the Saka Era plus 2526. (Requirement iii is given in the next stanza, XIII. 4, as one asterismal segment for 100 years).

Now TSN and KV argue thus: (a) This stanza is a quotation from Vrddha Garga (VG), and so VG knows a Saka Era which he mentions here. It is accepted by all that VG lived long prior to 78 A.D., the starting point of the Salivahana Saka. So this Saka must be an earlier Saka, viz., that of 550 B.C. postulated by them, (b) The first half of this stanza says the Sages were in Magha during Yudhisthira’s time. The Puranas and VG etc. say that at the junction of Dvapara and Kali yugas, the Sages were at Magha and Yudhisthira was ruling. 25 years after the advent of Kali, the Sages moved to the next asterism from Magha and in that year Yudhisthira left this world for heaven. The second half of the stanza states that the Sakakala mentioned therein started 2526 years after Yudhisthirakala. If we take Yudhisthirakala to have started from the time he went to heaven, i.e. after 25 Kali equivalent to 3076 B.C., this Saka must have started 2526 years after this, i.e. from 550 B.C., and is evidently quite different from the Saka starting from 78 A.D.

It is in the light of this conclusion, and in support of it, that TSN etc. say (as we have discussed already in the previous paper), that the Sakakala mentioned by VM in other places in his works, and also by other astronomers like Brahmagupta, is this Saka of 550 B.C. But we have proved conclusively in the previous study that in those places it is the Saka of 78 A.D. that is referred to.2 [There is one other place were VM mentions the Sakakala viz. dvyunam S'akendrakalam etc. (Pancasiddhantika, XII. 1), which we have not taken for discussion. This mention is in connection with the rough Paitamaha Siddhanta, and as no useful purpose will be served by discussing it, and as it is not taken into consideration by TSN etc. also, we have left it out.] Therefore the conclusion here arrived at by TSN etc. must stand on its own legs. We shall proceed to examine this now. Even at the outset we can say that it is extremely unlikely that VM means here alone a Saka different from what he means by the same word elsewhere in his works; and therefore he must mean the Saka of 78 A.D. here also. All the same we shall examine their arguments.

(a) The alleged quotation of Vrddha Garga

The reasoning (a) is based on the assumption that the stanza is a quotation from VG, which it is not. The actual words of VG are quoted by the commentator Bhattotpala in his commentary on this stanza: cf. tatha ca Vrddha-Gargah: “Kali-Dvaparayoh sandhau sthitas te pitrdaivatam” (At the junction of Kali and Dvapara, they—the sages—were at Magha). It is to be noted that this would be redundant if the staza in question also were VG’s, both giving the same idea, viz. the situation of the Sages. It may also be noted that this is in a different metre. What VM means by his statement in the introductory stanza, kathayisye Vrddha-Garga- matat (Br. Sam. XIII. 2) is only that he is giving the astrological predictions due to the motion of the Sages as based on the work of VG, as indicated by the word matat (‘opinion’) used here. Also in all the other caras given in the other chapters of Br. Sam, like Adityacara, Candracara, Rahucara etc., what VM means by cara is the prediction based upon the motion and not the actual motion, and so must it be here also, (the actual motions being given in a ganita work like the Pancasiddhantika). If in the case of the Sages the motion also is given, it is because it is simple, has not been given elsewhere, and is necessary for the main purpose, viz., the prediction according to the motion. Thus it is the prediction that VM says he gives according to VG. So this stanza which serves to find the position of the Sages need not necessarily be, and as we have shown, is not, VG’s.3 [This is the reason why this stanza has not been taken as VG’s by other scholars also. For e.g. Colebrooke writes: “The commentator, Bhattotpala, supports the text of his author (viz. VM) by quotations from VG and Kasyapa: ‘At the junction of the Kali and Dvapara ages’, says Garga, ‘the virtuous Sages ... stood...’ at Magha” (Miscellaneous Essays, London, 1873, vol. III, p. 313). Cunningham writes: “His (VM’s) words are, “The Seven Seers etc.,’ But unluckily for VM, his commentator Bhatta Utpala has given us the very words of Garga, who simply says, ‘At the junction of the Kali and Dvapara ages the virtuous Sages .... stood at the asterism over which the Pitrs preside, that is Magha'. On comparing this quotation with Varaha’s statement (in the stanza in question) we see at once that he (VM) has suppressed Garga’s mention of the Kaliyuga....” (Book of Indian Eras Culcutta, 1883, pp. 9-10). This shows, that Cunningham considers that VM is not quoting the stanza, but that it is VM’s own. P. V. Kane says: ‘In the preceding verse VM says that he will declare the motion of the seven sages by deriving it from the doctrine of VG. The first mistake of the writer (It is KV that he refers to here) is to hold that verse XIII.3 came originally from Garga Samhita. Really it is VM’s own verse. Utpala quotes the verse of VG, on this point, which is in a different metre, though the meaning is the same as the first half of XIII.3" (JAHRS XXI (1950-52) 41).] This being the case, it cannot be argued that Garga who came long prior to 78 A.D. knows a Sakakala and therefore this Sakakala must be the earlier postulated one of 550 B.C.

(b) The Time of Yudhisthira

We now pass on to consider (b), the second and more important reasoning of TSN etc., viz., that VM in this verse refers to Yudhisthira who lived at the beginning of of Kali and rose to heaven 25 years after Kali set in (i.e. in 3076 B.C.) and so the Saka Era beginning 2526 years after that must be the postulated Saka of 550 B.C. But we answer, there is nothing in this verse to show that in VM’s opinion Yudhisthira lived at the beginning of Kali. On the other hand, it can be shown that VM might have meant a time about 650 years after Kali, or even that he did mean this later period for the time of Yudhisthira, and therefore the Saka Era following 2526 years after, cannot be the postulated saka of 550 B.C., but can only be the well-known Saka of 78 A.D. It is a fact well known to scholars (inclusive of TSN etc.) that the junction of Dvapara and Kali (3102 B.C.) is not the only period with which Yudhisthira is associated. This is according to one school; but there is at least one other school ( e.g. that of the Jain and Buddhist writers) who take it that Yudhisthira lived about 500 years later. They use a Yudhisthira Era which began in 468 Kali (corresponding to 2634 B.C.).4 [Vide: i, Jinavijaya “rsir varas tatha purnam martyaksau (2077) vamamelanat” "nandah purnam bhusca netre maujanam (2109) ca vamatah” quoted by TSN in his Age of Sankara, (Madras, 1916 ff.), Pt. I. ch. iii, pp. 139 and 141, and also his adding 468 to get the year in the Kali Era. It has be added that TSN’s alleged quotations from this work are his concoctions. We have shown this in the ‘Date of Sankara” (see supra), ii Kota Bhaviah Chowdary’s statement: ‘According to Jain authorities Yudhisthira was crowned in 2634 B.C. only... From Puranic Kaliyuga (of 3102 B.C.).... 468 years passed up to Yudhisthira”. (JAHRS XXII (1952-54) 53 Cf. also Cunningham, Book of Indian Eras, p, 7, where he speaks of Abul Fazal giving in his Ain-i-Akbari three views on the subject, of which one is the regin of Kamsa, (uncle of Krsna and so contemporary of Yudhisthira) “above 4000 years before the fortieth of Akbar”, (i.e., 1595 A.D.), that is between 2400 and 2500 B.C.’ This would give Yudhisthira a date about 2407 B.C. or the 7th cent, in Kali.] Even of the first school mentioned, not all associate the same event of Yudhisthira’s life with the beginning of Kali, 3102 B.C. There are four sub-schools here (Fleet says three, but mentions all four, JRAS (1911) 676-78, ‘The Kaliyuga Era of B.C. 3102’). One sub-school believes that the first coronation of Yudhisthira at Indraprastha was the beginning of Kali and the commencement of the Yudhisthira Era.5 [The inscription in the temple of Hanuman at Jasalmer, Rajaputana, gives a date in this era. The speech of Hanuman in the Mahabharata, Vanaparva, ch. 151, verse 39 (Kumbakonam edn.) containing the words etat kaliyugam nama acirad yat pravartate, and Krsna’s excuse for the unfair fight with the words praptam Kaliy ugam viddhi (ib . S’alyparvan, ch. 61, verse 27) support this. Abdul Fazl expresses another view that the Mahabharata War was fought 4801 years before the 40th year of Akbar’s rule and 105 years before the end of the Dvapara age, (see ib).] Another makes the Bharata war and the beginning of Kali synchronous.6 [Eg. the Aihole Inscription. See discussion infra for details. This view is mentioned also by Abul Fazl, which is 4696 year before the 40th year of Akbar’s rule, (see ib).] A third says that Kali began at the death of Krspa and his ascent to heaven.7 [The Puranas express this view. Cf: yasmin Krsno divam yatah tasmin eva tadahani / ; pratipannah Kaliyugah tasya sahkhyam nibodhata //; Brahmanda Purana, ch. 74, verse 241 (Venk. Press edn.). Vayu has the same reading. Visnu, Matsya and the Bhagavata have almost the same reading.] The fourth sub-school says that Yudhisthira’s abdication and starting on the Mahaprasthana was at the beginning of Kali.8 [The words in the Aryabhatiya, Gurudivasac ca bharatat purvam, (Gitika, 5), which is explained by Paramesvara as ‘the day of the Mahaprasthana’, support this.] The reason why there are so many views must be explained by the fact that the traditional idea of the ages like Krta, Treta, Dvapara and Kali with their specific characteristics, was earlier than the integration of the beginning of the traditional Kali with that of the astronomical Kali answering to 3102 B.C., which was computed later by astronomers like Aryabhata so as to form a convenient point of reference for the Mean Planets. Thus the Kali Era, said to begin with 3102 B.C., is an extrapolated era, and in examining any date mentioned in this Kali Era, this fact should be borne in mind.

Now, in this multiplicity of schools on this point, which is a fact accepted by all, resulting from the integration of the traditional Kali with the astronomical Kali, there is the possibility of VM’s statement representing one other school or at least a variant of the Jain school, differing as it does, from it only by about two centuries. Kalhana, the Kashmirian chronicler of the 12th cent. A.D., is one of those that subscribe to this school; for not only does he quote in his Rajatarangini this verse of VM. but also expresses his own concurrence with it in so many words:

Bharatam Dvaparante ’bhud vartayeti vimohitah /
kecid evam mrsa tesam kalasankhyam pracakrire //
I.49//

***

satesu satsu sardhesu tryadhikesu ca bhutale /
Kaler gatesu varsanam abhuvan Kuru-Pandavah //
I.51 //

***

sat-dvika-panca-dvi-yutah Sakakalas tasy rajnas ca /
I.56b I//

“Some people have been misled by the statement that the Bharata (War) was at the end of Dvapara, and have given a wrong chronology to the kings (the Pandavas, Gonanda etc.) ... The Kurus and the Pandavas came when 653 years had passed in Kali... The time in the Saka Era plus 2526 is the time of his rule, i.e. the time in the epoch beginning from his (Yudhisthira’s) rule.”

It may noted that 653 plus 2526 (the numbers here given) equal 3179, the well-known converter of Saka into Kali and vice versa. Not only is Kalhana a believer in this school, but he is also certain that VM belongs to this school, as seen by his statement ‘Samhitakaraih' (Rajatarangini, I. 55) and his quotation of VM following immediately (I. 56). Cunningham also thinks the same as seen from his statement, “As VM places the Great War 653 years after the beginning of the Kali Age....” (op. cit. p. 11). Again, Prof. P. C. Sengupta, who in his Ancient Indian Chronology (Univ. of Calcutta, 1947) in seeking to determine the date of the Bharata War astronomically (see chs. I-IIl) favours this school, and comes to the conclusion that: ‘‘The date of the Bharata Battle is thus astronomically established as the year 2449 B.C. (Kali 653), which is supported by the Vriddha Garga tradition recorded by Varaha Mihira.,’ (see p. 19). Now it must be noted that the mere possibility of following this school is sufficient for our purpose, as we have stated above.

Nor, can the objection be raised that VG and the Puranas associate the Sages with Magha at the beginning of Kali, and that in this verse too, as the Sages are declared to be at Magha in Yudhisthira’s reign, the time here should be taken as the beginning of Kali, and so the time given for Yudhisthira’s rule must be the beginning of Kali, and not 653 Kali. For, the beginning of Kali is not associated with Magha alone. The Matsya Purana says (ch. 271, st. 41) that according to the Srutarsis the Sages were at Krittika at at the beginning of Kali, and TSN and KV are aware of it (TSN quotes it and explains it, see The Age of Sankara, Madras, 1916 ff., App., pp. 166-67; so also KV, Plot in Indian Chronology, 34-36). They themselves say that in VM’s opinion also the sages were at Krittika at the beginning of Kali (TSN. ib., p. 171; KV, ib. p. 36, and ‘Indian Eras’, JAHRS XX. 77).9 [In fact, nowhere does VM say that the sages were at Krttika at the beginning of Kali. This must be an inference of Cunningham when he gives (cf. Table on p. 17 of his Book of Indian Eras ) 3177 B.C. for the beginning of Krttika according to VM, inference from the fact that according to him the Sages passed to Magha in the 7th cent, after Kali (cf. same Table). TSN and KV seem to have simply taken Cunningham’s statement as true without question. They only object to Cunningham’s treating the motion as direct, while according to them it is retrograde. But they fail to see that if the motion is retrograde, the Sages should be at Anuradha (and not at Krttika) at the beginning of Kali, if they are to come to Magha seven centuries later. The Cunningham’s inference would be wrong and their acceptance of it would also be wrong.] According to Aryabhata II and Parasara too (for details see below), the Sages were at Krttika at the beginning of Kali. They were at Sravana according to Sakalya and Munisvara, and at Rohini according to Lalla (for details, see below). So the objection raised above does not stand. Now, according to Aryabhata II and Parasara, who give Krttika, it is easily seen that the Sages will be in Magha in the 7th cent. Kali, for Magha is the seventh asterism from Krttika and the motion is about one century per asterism. Thus, there can be no objection to the Sages being in Magha in the 7th cent. Kali. It is only if the motion of the Sages is taken to be retrograde (as TSN and certain others think) according to Aryabhata II, Parasara and VM, that the Sages cannot be in Magha in the 7th cent. Kali, but would be far away from it. But it is not retrograde according to Aryabhata II, Parasara and VM, as also according to other astronomers who give rules for the motion, which we shall show.

III. (a) ‘Motion of the Sages’—Direct, not Retrograde

This requires a knowledge of the motion of the Seven Sages10 [The following are the names of the Sages, with their Right Ascension and Declination for c. 1900 A.D.: (i) Kratu (Alpha Ursa Major) 10h 58m, +62° 17'; (ii) Putaha (Beta Ursa Major) 10h 56m, +54° 55'; (iii) Pulastya (Gamma Uras Major) 11h 49m, +54° 15'; (iv) Atri (Delta Ursa Major) 12h 10m , +57°; (v) Angiras (Epsilon Ursa Major) 12h 50m, + 56° 30'; (vi) Vasistha (Zeta Ursa Major) 12h 50m, +56°; (vii) Marici (Eta Ursa Major) 13h 44m, + 49° 49'. For comparison we shall give the asterisms belonging to the corresponding ecliptic segment: Magha (Alpha Lenois) 10h 3m , +12° 27'; Pur. Phal. (Delta Lenoise) 11h 9m , +21° 4', Ut. Phal. ( Beta Lenois) 11h 4m, +15° 8'; Hasta (Beta Corvi) 12h 29m, —25° 5'; Citra (Alpha Virgo) 13h 20m , —10° 38', Svati (Alpha Bootes) 14h 11m, +19° 42'.] which we shall give in some detail because there is a lot of misconception among scholars (including TSN, KV and VT) about this, which in turn vitiates the results of their researches. It was believed by the authors of the ancient Jyotisa Samhita, like VG, that the Sages had a motion of their own among the other stars, just like the planets, the rate of motion being given as 100, or nearly 100, years per asterism (13° 20'). It may be said, even at the outset, that there is no such motion as claimed to exist by the authors of these Samhitas and followed up the Puranas and some of the later astronomers; that the Sages are always to be associated only with the Phalgunis, Hasta and Citra asterisms (see fn. 10); and that the theory of their motion is wrong, howsoever it might have originated.11 [(i) A number of explanations can be given as to how this wrong theory of motion could have originated, but as this is beside the point, we stop with saying this much. Some people believe in the reality of this motion and try to explain it accordingly, using the theory of the Precession of the Equinoxes. For e.g. (i) VT says that because the celestial Pole moves in a small circle once round the Pole of the Ecliptic in about 27,000 years, the point of inter-section of the Ecliptic with the line joining it and the mid-point of the first two stars constituting the Sages also moves. As the Sages are said to be at this point of intersection, they are also considered to move (see his Popular Astronomy, Madras, 1958, pp. 138-40). But this simulated motion can be only a small fraction of of the value of the motion according to the Samhitas which is as great as 13° 20' per century. Also, while the Samhitas say that the motion is uniform and traverses the ecliptic completely, this simulated motion will not be uniform, and will be oscillatory and restricted to a small segment of the ecliptic. Thus it will be forward and backward, the former during the past 7,000 years and more, against the opinion of VT ( cf . ib., p. 139) who says that the motion is retrograde like that of the First point of Aries. (ii) Prof. R. Krishnamurti (according to VT, ib. 139-40) holds the view that the extent of the Sages in longitude is about a tenth of the ecliptic. This extent is divided into 27 equal parts, each part ‘symbolically’ forming a Naksatra. The traversing of these 27 symbolic Naksatras will take 2700 years. If it is taken that the other 9 segments also are so divided, it will take 10x2700=27,000 years for traversing the whole ecliptic. According to him, the authority for this symbolic division is the following in the Rgveda: satm te rajan bhisajas sahasram urvi gabhira sumatis te astu / ; badhasava dure nirrtim paracaih krtam cidenah pramumugdhyasmat // ; ami yo rksa nihitasa ucca naktam dadrse kuhacid diveyuh / adabdhani varunasya vratani vicakasaccandrama naktam eti // Rgveda 1.24.9-10. But what have these rks in prayer of Varuna to do with the alleged symbolic division? What flight of imagination can create the idea of the symbolic division of the ecliptic from the two words satam and sahasram in one sentence, and the word rksa i n quite a different sentence? And then Prof. Krishnamurti seems to suggest that the motion of the Sages is only another name for the phenomenon of Precession, artificialised for the purpose of chronology. (iii) Dr. D. S. Triveda (JIH XIX (1940) 9-12) confuses the motion of the Sages with Precession itself and says that the ancient rsis, far older than Samhitakaras, had discovered a cycle of 27,000 years for the motion (the same as for Precession), but by the time of the Samhitakaras one cypher was lost, and the period was mistaken as 2700 years! He does not mention how Precession simulates the motion of the Sages.] That is why many standard astronomers and astronomical works like Aryabhata I, Brahmagupta, Sripati, Bhaskaras I and II, the Suryasiddhanta, etc., do not deal with the subject at all as being outside the pale of real astronomy. That is also why Kamalakara is constrained to say in his Siddhanta Tattvaviveka (Banaras, 1880-85), Bhagrahayutyadhikara:

Sakalyasamjna-munina kathitas sabanah
saptarsitarakabhava dhruvakas calais ca / 25a /

***

yair golatattvam vivrtam hi tais ca
suryadibhir naiva visesa esah /

proktas svasastre 'sti gatir muninam
ato na yukta divi golaritya // 30 //

* * *

adyapi kair api narair gatir aryavaryaih
dysta na yatra kathita kila Samhitasu / 32a /

* * *

prayo ’tha te ca munayah kila devatamsa
drggocara nahi nrnam iha satphalaptyai /36 /

“Sage Sakalya has given the motion of the Sages with their positions in his time...Surya and others who explain the nature of the celestial sphere in their works do not give it and therefore the theory cannot be sustained astronomically...Even today this motion mentioned in the Samhitas is not observed by knowing astronomers... Therefore the seven real Sages who are (only) the presiding deities (of these stars) are to be considered to be moving, unobserved by men, for the prediction of the fruits thereof.”

But the motion has been accepted as a fact by the common people and the authors of the Puranas, and an era called Laukika Era (by the people belonging to the Kashmir region) and the Saptarsi Era (by the Puranas), has been founded upon this theory.12 [We do not know when these eras were founded. The Puranas say that 25 years after Kali set in, the Sages who had been at Magha for 100 years left it for the next asterism. The dates of the dynasties of kings are given in terms of the situation of the Sages in the different asterisms. The Laukika Era is the same as the Saptarsi Era with the number of the year in each century being generally used and the centuries or the reference to the asterisms omitted. This is used in the Rajatarangipi to give the dates of dynasties and kings, as also the date of the work.] As already mentioned, there are also astronomers like VM, Aryabhata II (cf. his Aryasiddhanta or Mahdsiddhanta, Madhyamadhyaya, 11), Parasara (cf. Aryasiddhanta, Parasaramatadhyaya, 9), Lalla (quoted by Munisvara in his commentary on the Siddhanta Siromani), Sakalya (quoted by Munisvara, ib., and by Kamalakara in his Siddhanta Tattvaviveka, Bhagrahayutyadhikara 25 and under), Vatesvara, and Munisvara (see his Siddhanta Sarvabhauma), who have accepted the motion as real on the authority of the ancients and given rules for the motion, which necessarily must agree with their own observation, or else they would be meaningless even for them.13 [vide Colebrooke, ib., p. 316-17: ‘‘...a probable inference may be thence drawn as to the period when these authors lived, provided one position be conceded; namely, that the rules, stated by them, gave a result not grossly wrong at the respective periods when they wrote. Indeed, it can scarcely be supposed that authors, who, like the celebrated astronomers in question, were not mere compilers and transcribers, should have exhibited rules of computation, which did not approach to the truth, at the very period when they were proposed.”] This means that whatever be the rule, if applied to the time of the author, the position of the Sages must be got as between Magha and Svati.14 [Because the Sages are always to be seen within this limit. Though strictly speaking the position of the first two stars are to be taken into consideration, still, in practice, the situation of the whole group must have been vaguely taken as the position. The Sages are said to be at the asterism where the declination circle passing through the mid-point of the two front stars (Pulaha and Kratu) that rise first, cut the ecliptic. This would give a position beyond Magha and near Purva Phalguni, at present. (But in ancient times Magha might well have been the position an account of the Celestial Pole having been a little more to the East of its present position.) But it seems that later on it came to be considered that the asterism against which the Sages are seen generally is the position. Thus we can get Purva Phalguni, Uttara Phalguni, Hasta or Citra. The rule may also be interpreted as the segment which is seen to rise together with the two front stars. If this interpretation is accepted, we can get, on account of cara (oblique ascension), any asterism from Krttika to Magha as the position for observers in North India according to their latitude.] In giving the rules, the authors all consider the motion as direct and never as retrograde as fancied by some scholars like TSN, KV, VT etc, for which fancy there is no support anywhere.15 [The idea of the retrograde motion must have originated very late, the reason being that it can, at that period, serve to reconcile faith in the theory of the motion with observation. (Giving various positions like Magha, Krttika, Rohini, Sravana, to the Sages at the beginning of Kali, giving different rates of motion, and being satisfied with rough positions, are evidently only different means of effecting this reconciliation). The Pandits of Banaras who informed Col. Wilford in c. 1804, believed in the retrograde motion. The Kaliyugarajavrttanta, (Bhaga. Ill, ch. iii), as quoted by TSN, KV and VT, undoubtedly believes that the motion is retrograde, by stating that 25 years after Kali set in, the Sages left Magha for Aslesa (See Age of Sankara, Pt. I, App., 139ff; JAHRS XX. 62ff; JAHRS XXII. 169-70). But as can be seen from the dynasties it deals with, it is a recent work, and cannot command authority like the Puranas, for the author of this work is not known and may be only like one of us trying to reconstruct ancient history from Puranic evidence. ] Let us take the rules one by one and examine them for the facts mentioned.

VM’s rule is as follows ( Br. Sam., XIII. 3-4): The number of years gone from the time of Yudhisthira is to be found by adding 2526 to the Saka years gone at the time for which the position of the Sages is wanted. This is to be divided by 100, which gives the number of asterismal segments gone, and these are to be counted from Magha to get the position. In the context there is no mention of any retrograde motion, nor is it mentioned that the number got is to be counted backwards as in the case of the patas like Rahu. In the absence of any such specific indication we do what is normally done, i.e., count the segments forward, as in the case of all other grahas like the Sun etc. Working for VM’s time, i.e., 427 Saka, we get the middle of Uttara Phalguni as the position of the Sages, which is well within the limit for agreement with observation. If we count backwards taking the motion as retrograde, we get the middle of Pusya, which is far outside the limit, and this also shows that the rule implies only forward motion, as we have already determined.

Arybhabhata II gives the rule in the form of cycles per Kalpa, even as the Siddhantas do for the planets. He says there are 15,99,998 cycles in the Kalpa and the cycles commence 30,24,000 years from the beginning of the Kalpa. Here too there is no indication of retrograde motion. Calculating from the above date we find that at the beginning of the present Kali the Sages are at 2 38 segments (counting from Asvini), i.e., they have passed Bharani and been in Krttika for 38 years. It is easily seen that at 662 Kali the Sages will cross to Magha according to this Siddhanta. Compare this with VM’s rule that would give the crossing to Magha in the 7th century Kali (exactly speaking 653 Kali; for going back 2526 years from zero Saka, equal to 3179 Kali, we arrive at this date).16 [For c. 700 A.D. the position of the Sages would be Citra, which, being within the limit of observation, we can conclude that the date of Aryabhata II is c. 700 A.D. Though a date within three centuries earlier is possible, it is not likely; a date as late as can be within the possible period has to be fixed for Aryabhata II on other grounds.]

We now pass on to Parasara. His rule is the same as that of Aryabhata II, with the difference that in Parasara’s case the cycles begin at the commencement of the Kalpa itself. This would give for the commencement of Kali the position 2 34 naksatras, counting, of course, from Asvini, i.e., after crossing Bharani, the Sages have been in Krttika for 34 years, and at 666 Kali the Sages pass on to Magha.17 [For details see Mahasiddhanta, Ed. Sudhakara Dvivedi, Banaras, 1910, Contents in English, pp. 1-4. See also Cunningham, ib., p. 8.] See how close this is to 662 and 653, the dates according to Aryabhata II and VM, derived above.18 [Obviously, the probable date of Parasara would also be c. 700 A.D. or within some three centuries earlier. This would give sufficient time for Aryabhata II to refer to Parasara’s views in his work.]

Now for Lalla’s rule: As said before, the rule is quoted by Munisvara in his commentary on the Siddhanta Siromani. It is this: Deduct 14 from the Kali years gone and divide the remainder by 100. Asterisms are got, which are to be counted from Rohini.19 [Lalla uses the word virinci (a synonym for Brahma or Prajapati). All but Munisvara take this as Rohini, and this would give the Sages a position agreeing with observation in Lalla’s time, c. 650 A.D. But Munisvara, in order to make it agree with his own observation, takes it as Abhijit (whose deity is Vidhi, another synonym for Brahma), which is almost the same as Sravana. Naturally, Munisvara is unaware that for Lalla’s observation it is Rohini that would give the agreement. He seeks support for his interpretation from Sakalya Samhita, Prasna II, ch. ii, the statement, “Kratu was at Visnu’s star at the beginning of Kali.”] Here too it is to be noted that no backward counting is enjoined, and the rule must normally mean forward counting as in all rules where nothing is said. It is to be noted that according to this rule, the Sages pass to Rohini from Krttika, 14 years after Kali set in, i.e., they have been in Krttika for 86 years before the beginning of Kali, (agreeing with VM within half a segment). Taking the date of Lalla to be 650 A.D.,20 [It has been shown in the Introduction to the Mahabhaskariyam (Ed. T. S. Kappanna Sastri, Madras, 1957), p. xviii, that Lalla is later than Brahmagupta, having commented upon his Khandakhadyaka, and so he could not have been a disciple of Aryabhata I, and so not much earlier than 650 A.D.] the Sages would be at Citra in his time.

According to Sakalya Samhita, “Kratu, one of the Sages, enters Sravana at the commencement of Kali and the Sages have direct motion every year at the rate of 8' (which rate is equivalent to one asterism per century);” cf.

yugadau visnutarayah kratur bhadye vyavasthitah /
pratyahdam “praggatis” tesam astau lipta Munisvara //

(Quoted in Kamalakara’s Com. on his own Siddh. Tat. Viv., Bhagrahayutyadhikara, under stanza 25)

According to Vatesvara, Madh. 15,
[x] // 1692 //

So the rule would be to multiply the Kali years by 8 and divide by 800, to get the asterisms. These are to be counted forward from Sravana. It may be noted that here eastward motion, i.e., direct motion, is specifically stated. Kamalakara, too, explaining the motion as really that of the presiding sages, says in the same context that the motion is eastward, i.e., direct; cf., sa praggatir munivarair bhagata muninam (ib., 36). According to this rule, after 1100 A.D. the Sages would move to Magha, and we can place this work at the earliest in c. 1100 A.D.

Lastly, for the rule of Munisvara given in his Siddhanta Sarvabhauma. Deduct 600 from the Kali years. Double the remainder and divide by 15. The position of of the Sages in degrees in got. This divided by 30 gives the position in the rasis. This rule again clearly takes the motion as direct. According to Munisvara the Sages cross to Asvini at 600 years Kali (which is equivalent to the statement of Sakalya, for according to Sakalya’s rule too the Sages enter Asvini at 600 Kali). At the time of Munisvara, according to his own rule, the Sages would have crossed from Citra to Svati which is just outside the limit, and which position Munisvara should have accepted as agreeing with observation because the difference was not much. (It would have satisfied him better if some astronomer had said or if he could obtain, by quibbling, the Sages were at Sravistha or Satabhisak at the commencement of Kali. No such thing was available, and the best he could have was Sakalya, and he had to be satisfied with that).

Thus all authorities either state or imply only direct motion, and there is no authority for retrograde motion. That is why scholars like Cunningham (as already mentioned), “Sriyut Sris Chandra Vidyarnava, Dr. Jayaswal and many others” (in the words of Dr. Triveda, JIH XIX, 11) have considered the motion direct. There may be some like “the most famous astrologers of Banares who informed Col. Wilford”, (cf. Triveda, ib., p. 10), and the author of Kaliyugarajavrttanta who believe the motion to be retrograde. But in the light of what we have said, they must be wrong (see Fn. 15).

III (b). The Puranas on the motion of the Sages

Also, the Puranas do not say whether the motion is direct or retrograde. We cannot get any indications regarding the direction of the motion of the Sages from the Puranas themselves, as they are vitiated by emendations and interpolations, made to affect the very point which we are trying to decide. Still, some scholars resort to them for support, and it is not surprising that they fail to establish anything. Dr. Triveda is one such:21 [Cf. his article, “The Intervening age between Parikshit and Nanda', JIH XIX (1940) 1-16.] he not only does not prove his point, but proves the contrary of what he desires to prove, as also the lack of clearness in his mind. For e.g.: He says: (i) “But in fact their (the Sages’) motion is retrograde as from the word Precession, pre= purva or east, and cession from Fr. cedare— go” (ib., p. 11). (ii) “Kamalakara Bhatta also says in his Siddhanta Tattvaviveka, ‘pratyabdam praggatis tesam’; that is, in every year their motion is from West to East.” (ib. p. 11). (iii) “C. A. Young in his A Text Book of General Astronomy published in 1904 says on page 141, ‘The Equinox moves westward on the ecliptic, as if it advanced to meet the Sun on each annual return’. So it is certain that their motion is contrary to that of the Sun, and it is retrograde.” (ib., p. 11)

Let us examine his statements here, (i) If Precession is retrogade, why should the motion of the Sages be retrograde also? Are they the same phenomenon? If he means that the motion is derivable from Precession, he has not shown it, and cannot show it, because it is not so (see Fn. 11 (i) above). Even if some connection be established between the two, in the period we are considering the simulated motion would be directed only opposite to Precession (see Fn. 11 (i). He is not aware that the derivation he gives for the word ‘Precession’ would mean direct motion even for Precession, and not retrograde motion, for ‘going east’ means ‘direct motion’. (ii) Dr. Triveda’s quotation from Kamalakara is plainly against himself, for 'from west to east’ is 'direct motion’, and not otherwise as Dr. Triveda thinks, (iii) Young rightly says that the Equinox moves westward, i.e. it has retrograde motion. But what has that to do with the Sages? Triveda does not perceive that from here it can be understood that it is westward motion that is retrograde, and not eastward motion, as he thinks.

Under the delusion that he has proved the motion of the Sages to be retrograde, Dr. Triveda proceeds to apply this to the following statement in the Puranas in order to establish his thesis that the interval between Pariksit and Nanda is 1500 years (given by one reading) and not 1015 or 1050 years (given in certain other readings (cf. Triveda, ib., pp. 1-3, 12-15). We shall briefly examine this in order to expose the errors in his reasoning, for if he establishes his point by using his theory of retrograde motion, that might be taken by some as a point in favour of the theory of retrograde motion itself, even after all that has been said by us to establish that the motion is direct.

The Puranic statement is as follows:21a [See the text and the variants recorded by Pargiter, The Purana Text of the Dynasties of the Kali Age, O.U.P., 1913, p. 58.]

Mahapadmabhisekat tu yavaj janma Pariksitah /
(or yavat Pariksito janma yavan Nandabhisecanam /)
evam varsasahasram tu jneyam pancasaduttaram
(1050) //

The last foot has the variants: Satam panca dasottaram (i.e., 1510) or pancadasottaram (i.e., 1015) or pancasatottaram (i.e., 1500) (Visnu Purana, IV. xxiv. 104; Bhagavata, XII. ii 26; etc.). Triveda’s thesis is to establish the interval to be 1500 or 1510 (according to two readings given) using the Saptarsi Era given in the following Puranic statement:22 [See Pargiter, ib., p. 62. In the place of this line mentioning Purvasadha, the Kaliyugarajavrttanta gives: Sravane te bhavisyanti kale nandasya bhupateh. This is not supported by any Puranic source and hence not fit to be taken as authority.]

prayasyanti yada caite purvasadham maharsayah /
(or yada maghabhyo yasyanti purvasadham maharsayah) /
tada Nandat prabhrtyesa Kalir vrddhim gamisyati //
(Visnu Parana, IV. xxiv. 112; Bhagavata, XII. ii.32; etc.)

It is said here that when the Sages pass from Magha, (their position at the beginning of Kali when Pariksit was ruling), to Purvasadha at the time of Nanda, the Kali will worsen. From Magha to Purvasadha the Sages pass 10 asterisms in their course, taking the motion to be direct, (as we have established), i.e., about 1000 years from Pariksit to Nanda (or 3700 years if one cycle has gone), and this is supported by two readings. But Triveda suggests 1500 years for this interval, supported by the other two readings. Counting backwards from Magha to Purvasadha (in accordance with his theory of retrograde motion) he should get 17 asterisms, not counting either Magha or Purvasadha and at least 16, not counting both. Thus he should get at least 1600 years as the interval. But this will not suit his theory, and so he omits to count Sravana, and gets the 15 asterisms he wants, to give him the required interval of 1500 years! (see ib., p. 12, lines 10-11). This is proof that the author of the Puranas, who employed the Saptarsi Era for purposes of chronology, has taken the motion only to be direct and used the Era; and not retrograde, for if taken as such, at least 1600 years will be got as the interval, which is not supported by any reading of the text.23 [On page 13 of his article, Triveda gives a tabular statement of the chronology. There he counts Sravana, but to compensate for the extra 100 years that would occur, gives the period 3233 to 3133 B.C. for Magha and 3133 to 3076 B.C. for Aslesa, (this giving only 57 years for Aslesa instead of 100) against the Puranas that give 3176 to 3076 B.C. to Magha, 3076 to 2976 B.C. for the next star and so on. Triveda's scheme is supported by no Purana. Incidentally we may mention another mistake he employs to achieve his purpose. He wishes to give 1724 A.D. to 1824 A.D. for Svati (see p. 15), so that his table might agree with the statement of Wilford’s Pandits of Banaras who have told that the Sages were at Svati in 1804 A. D. So he includes Abhijit among the Naksatras counted and gives for it the century 1024 to 1124 A.D. (see p. 14), apparently unaware of the fact that this trick would make the cycle last 2800 years instead of the usual 2700 years, and that he himself has not counted it in the previous cycle (see p. 13). If this kind of trick is resorted to one can prove anything!]

One thing clearly emerges from this discussion, viz. that the motion of the Sages as given by the astronomers and the Puranas is direct and not retrograde. So VM can be right in saying that the Sages were in Magha in the 7th century Kali and in this he is supported by Aryabhata II, and Parasara, as well as the Srutarsis. Therefore Yudhisthira’s reign associated with the Sages at Magha can well be in the 7th cent. Kali, also supported as it is by a whole school of chronologists. As the Saka Era mentioned is to come 2526 years after this period, it is the Saka of 78 A.D. that must have been meant by VM in the sloka. Br. Sam. XIII. 3, and not the one postulated by TSN etc., concurring with what we have established already in the previous study from an astronomical point of view.

IV. The Aihole Inscription

Now we shall take up the Aihole Inscription and show that the Saka used in it is only that of 78 A.D. and not the other one alleged by TSN and echoed by certain other scholars. Discussing the age of VM in his Age of Sankara, Pt. I-D, pp. 224ff., TSN takes up the Aihole Inscription for consideration,24 [We have not had access to this section of TSN's work. Our authority is the long quotation in KV's Plot in Indian Chronology, ch. X. 185-90.] and tries to show that the Saka Era mentioned therein is his own Saka of 550 B.C. from the synchronism found in it between the Saka Era and the Bharata War. The portion of the inscription relevant to our discussion is the following:

trimsatsu trisahasresu bharatad ahavaditah /
saptabdasatayuktesu sa (?ga)tesvabdesu pancasu /
pancasatsu Kalau kale satsu pancasatasu ca /
samasu samatitasu Sakanam api bhubhujam //

In trying to interpret this passage, Dr. Fleet at first (Indian Antiquary, V (1876) 67-73) made the mistake of thinking that the time of the inscription is given in three eras, viz. Bharata War, the Kali and the Saka. Perhaps he was led into this mistake by the word ‘sata’ occurring thrice (saptabatatayuktesu, satesvabdesu, and pancasatasu) and the statement in the Puranas that the Kali epoch is different from the Bharata War. But subsequently, in IA VIII (1879) 240-41, Dr. Fleet acknowledged his mistake and gave the correct reading by emending satesu into gatesu (for, in the Kanarese-Telugu script in which the inscription is engraved on rock, ga, with a horizontal stroke across would become sa and the engraver might have been misled into adding the stroke here by the large number of sa letters occurring the context; or it might have been caused by weathering) and interpreting the passage as 3735 years from the Kali epoch, after the Bharata War, and 556 years after Saka kings, i.e. 556 years in (Salivahana Saka Era.25 [This Era is variously given as sakanam nrpanam (or bhubhujam) kala, sakanrpati) (or bhupa) kala, sakendrakala, in the earlier centuries and as Salivahana Saka later. The origin is also attributed to various causes: e.g. as named after the good rule of the Saka kings (Govindasvamin’s Bhasya on Mahabhaskariya), the destruction of the Sakas by Vikrama (Bhattotpala commenting on Br. Sam. VIII. 20), and after Salivahana who established his rule (later commentators and tradition).] This interpretation is accepted by all scholars (see for instance, Kielhorn, Ep. Ind., VI (1900-01) 1-12), except TSN and KV.26 [After siding with TSN in The Plot in Indian Chronology, ch. X, and speaking with some variation in JAHRS XXI (1950-52) 52-53, K.V, has changed over to the correct interpretation in his note, ‘The Aihole Inscription of Pulikesin’, (JAHRS XXII (1952-54) 210-12, wrongly numbered 206-08) without a word of regret for having talked lightly and questioned the bonafides of the very persons to whose opinion he has now been converted. On p. 212, he still seems to be unaware of the fact that Dr. Fleet has corrected himself long ago.] But the emendation of satesu into gatesu is accepted by TSN. He also accepts the fact that only two dates are given, of which one is Saka Era. This necessitates the two expressions ‘after the Bharata War’ and ‘from the Kali epoch’ to be taken together, as giving one date. If the Kali epoch is meant as important and the Bharata War is mentioned here simply to describe it, without any more trouble we get the interpretation, ‘3735 years from the Kali epoch’, which beautifully synchronises with the Salivahana Saka year 556 given, (about this number there is no dispute), for if we deduct from 3735 the well-known converter 3179 we get 556, which itself proves that this must be the Salivahana saka of 78 A.D. If, on the other hand, the Bharata War is taken as important, and also that the War was fought 36 years earlier (TSN makes it 38 to suit his calculations) according to one sub-school27 [See fn. 7 supra. Note that there is still another sub-school that takes the war synchronous with the Kali epoch. Obviously according to this school also, the interpretation is what we have already mentioned as the correct one.] taken advantage of by TSN, then there is trouble, for the War took place in 3140 B.C. according to TSN. 3735 years from this date there is no Saka epoch to synchronise with. But TSN sorely wants it to synchronise with the Saka of 550 B.C. postulated by him. He clutches at an error committed in a collection of old records published for literary study, the Pracinalekhamala, (N. S. Press, Bombay, Kavyamala Series 16), thinking that it will help him. In the Pracinalekhamala, saptabdasata is printed as sahabdasata. Whether this is a misprint or an intended emendation, we do not know. But this much we can say, that the letter is certainly pta and not ha, as anyone can verify from the photo-print of the inscription reproduced in IA V (1876) op. p. 69, ib. VIII (1879) op. p. 241, Ep. Ind. VI (1900-01) op. p. 7, etc.) and comparing the letters. Not only this; the word saha will be a repetition, because there is the word yukta giving the same meaning; also saha requires an instrumental to govern, which is not available in the verse. In spite of all this, TSN takes this saha instead of sapta and gets the number 3135, of course, as we have pointed out, with a duplicate saha serving no purpose in the interpretation) and begins to effect the synchronisation thus (see p. 189, Plot in Indian Chronology): The Aihole Inscription is 3135 years from the War, viz. 3140 B.C. So the date of the inscription is 5 B.C. And then the inscription is 556 years from the Saka epoch (of TSN), viz. 550 B.C. 556 years from 550 B.C. is 6 B.C. (so says TSN, for he wants it, and wish is father to thought). 6 B.C. is only one year off 5 B.C. (obtained above), which can be easily accounted for, and the synchronism established; which shows that the Saka mentioned in the inscription is his Saka of 550 B.C. But TSN and KV who quotes him seem to be unaware of the blunder in the calculation, and that 556 years from 550 B.C., is not 6 B.C., but 7 A.D.; and this date is 11 years off 5 B.C., and no amount of jugglery can spirit this period of 11 years off and the synchronism is far from being established. What is more, having failed to prove the 550 B.C. Saka, but thinking that it has been proved, TSN indulges in a tirade against Orientalists and their ways (see p. 190, ibid.), unconscious all the while, that it all applies to TSN himself!: “Alas! it is a great pity that these Orientalists should at first conceive a theory of their own, and then actively set themselves to work out the same by hook or by crook, by changing every authority to suit their own favourite hypotheses, and by hoisting up the fabricated text as the only true version, while they perfectly know all the while in their own heart of hearts that they have been able to achieve their objects only by fabricating evidence and meddling with the original authorities. The Orientalists simply beg the question, and beat about the bush in discussing such matters (here, explanation of the word Saka), blowing hot and cold at the same time, misjudging themselves,  and misleading others, and thereby keeping back the Truth as far away as possible from the ken of ordinary public,” How aptly these words apply to TSN himself!

V. The Evidence of the Jyotirvidabharana

Even though we have stated that the evidence of the Jyotirvidabharana does not merit any consideration (see previous paper), still because it is made much of by TSN, KV and VT (see for e,g., KV: JAHRS XXI (1950-52) 28-32, Chronology of Nepal History, Vijayawada, 1953, pp. 14-19; VT: JIH XXVIII (1950) 107-08), we shall consider that too. Their contention is that the author of the Jyotirvidabharana is the famous Kalidasa himself as claimed by the work, that he with VM and several other great scholars lived at Vikramaditya’s court,28 [Cf. the verse Dhanvantari etc. Jyotir, XXII. 10.] that he wrote the work in Kali 3068 (34 B.C.),29 [Cf. varse sindhuradarsanambaragunair (3068) yate Kalessammite / mase Madhavasamjnike ca vihito granthakriyopakramah // XXII. 21.] and that therefore VM cannot belong to 427 in the Saka of 78 A.D. (corresponding to 505 A.D.), but only in the postulated Cyrus (or Andhra) Saka of 550 B.C. (corresponding to 123 B.C.), and that thus the Cyrus (or Andhra) Saka is proved. But the work could not have been written before 78 A.D., (though it says it was written in 34 B.C.), for in that work Salivahana is mentioned as a saka-kara (founder of an era), and that he founded the Saka Era 135 years after Vikrama founded his own Saka 3044 years after Kali ( i.e. 57 B.C.).30 [Cf. Jyotir. X. 110-11, giving the several Eras of the Kali Age: (i) Yudhisthira Era for the first 3044 years, (ii) Vikrama Era for the next 135 years, (iii) Saka Era for the next 18000 years, (iv) Vijaydbhinandana Era for the next 10,000 years, (v) Nagarjuna Era for the next 400.000 ) ears, and Bali Era for the following 821 years.] How could Kalidasa, the alleged author of the work, be the contemporary (however junior it might be) of VM (said to have lived in 123 B.C.) and at the same time know the starting of the Salivahana Saka in 78 A.D.?

The late date of the Jyotirvidabharana can be established also by other internal evidence in that work. Thus in giving the rule for the calculation of ayanamsa, it is stated that 445 is to be deducted from the years in the Saka Era and the remainder divided by 60. Cf.

Sakah sarambhodhiyugo (445) nito hrto
manam khatarkair (60) ayanamsakas syuh / (1.18a)

This means that in 44 Saka the ayanamsa is zero. This can be only the Salivahana Saka, for Indian astronomical works give zero ayanamsa for c. 421 Sali. Saka (Kali 3600), (some give 444). It cannot be argued that the author means the postulated Cyrus Era here, because firstly among the six sakas given by him he does not mention this saka at all, and secondly nobody gives zero ayanamsa for this time (445 Cyrus Era would be 105 B.C.) not even VT, who, as we have seen, implies —3° 20' ayanamsa for 123 B.C. (though he takes it as the starting point for calculation) (see JIH XXVIII. 106) and our discussion on it in the previous paper). Thus, having seen that it is the Salivahana Saka that the author uses, we can say that he is later than 445 of this Saka, (523 A.D.), for this rule can be applied only later than 445 Saka, no instruction being given as to what to do if the time taken is before 445 Saka.

Again, the rule given in the Jyotirvidabharana for finding the year in the 60-year cycle of Jupiter corroborates this.31 [Cf. the rule: nagair nakhais sannihato dvidha sakah ; sakhatrisakro 'ksayamangabha jitah / ; gataptatallabdhasako 'bhrasadhrto- ; ’vaiesake syuh prabhavadivatsarah // (I. 15) . It means: 'Do the operation, {(7x+20x:/60 + 1430) divided by 625 + x} divided by 60, where x is the Saka year gone. Get the remainder. Count years from Prabhava equal to the remainder and the prabhavadi-year is got.’] If it is applied to the current year, 1881 Saka (1959-60), we get the year Virodhikrt, which we also get if we work it out according to the methods in the Siddhantas. If the year reckoned in the Cyrus Era or if the Vikrama Era is used in the rule, there is disagreement. So it is the Salivahana Saka that is required to be used in this rule and not the Cyrus Saka nor the Vikrama Saka which reigned in his time (for he says he is a contemporary of Vikrama). Thus, again, the conclusion that the author is later than the starting of the Salivahana Saka follows, and his use of that saka.32 [This kind of work we have already done, when dealing with Prof. Gulshan Rai. (See previous paper).]

In answer to these objections KV seems to have argued that Kalidasa could actually have lived earlier than the Salivahana Saka epoch and have mentioned that epoch as a future historical event on the basis of the Sastras33 [Vide his letter to Kottah Bhavaiah Chowdary referred to in JAHRS XXII. 55.] (evidently meaning the Bhavisya Purana etc.). But then how did the sastras know? Does KV want us to believe that they actually predicted future events? Clearly the sastras themselves should have been written after the Salivahana Saka epoch, and the Jyotirvidabharana should be later still. And the jumbling of people of various ages already alluded to! We are asked to take this bundle of lies as sober history!

In the same manner other romances, like the Kathasaritsagara, Bhojaprabandha, Vikramarkacarita etc., (there is no dearth of them) based on popular stories should be dismissed wherever they contradict what may be judged as solid evidence, for we do not know who their authors were, nor what equipment they had for giving historical facts.  

VI. Conclusion

Thus in all places where the word Saka is used for the name of an era, it is the Saka of 78 A.D. (what latterly came to be called Salivahana saka) that is meant. Further, there is no evidence to show that an era was started in 550 or 551 B.C. in Persia or in India as postulated by TSN and accepted by KV, which he calls the Cyrus Era, or as postulated by VT, which he calls the Andhra Era. It may be that Cyrus founded the Persian Empire in 550 B.C., but what evidence is there to show that he started an era then? No such era was in use in Persia itself, not to speak of India. Many great events happen in the reigns of great kings. But they are not necessarily the starting points of eras. (VT does not even mention a great event in 550-51 B.C. for the starting of his Andhra Era). Now, these people have taken all this trouble in order to prove the antiquity of the Indian dynasties and, in so doing, to reconcile texts of varied historical worth. Let them by all means attempt it for it is only too true that unconscious prejudice has had some hand in the writing of the history of our land. But what we wish to show here is that their stand on the interpretation of the term Saka Era, with all its ramifications, is wrong, and will not help them, as also the various other ideas of theirs which we have shown to be wrong. Also we wish to point out that attributing base motives and questioning the bona fides of people (the writings of TSN and KV are replete with these) will not only not help, but may also be “paid back with interest”, as Dr. P. V. Kane says.  

[admin]

Determination of the Date of the Mahabharata: The Possibility Thereof, [Reprinted from Vishveshvaramand Indological Journal, Vol. XIV (1976) pp. 48-56.], Excerpt, from Collected Papers on Jyotisha
by T.S. Kuppanna Sastry (Former Hony. Professor, Sanskrit College, Madras)
1989

NOTICE: THIS WORK MAY BE PROTECTED BY COPYRIGHT

YOU ARE REQUIRED TO READ THE COPYRIGHT NOTICE AT THIS LINK BEFORE YOU READ THE FOLLOWING WORK, THAT IS AVAILABLE SOLELY FOR PRIVATE STUDY, SCHOLARSHIP OR RESEARCH PURSUANT TO 17 U.S.C. SECTION 107 AND 108. IN THE EVENT THAT THE LIBRARY DETERMINES THAT UNLAWFUL COPYING OF THIS WORK HAS OCCURRED, THE LIBRARY HAS THE RIGHT TO BLOCK THE I.P. ADDRESS AT WHICH THE UNLAWFUL COPYING APPEARED TO HAVE OCCURRED. THANK YOU FOR RESPECTING THE RIGHTS OF COPYRIGHT OWNERS.

DETERMINATION OF THE DATE OF THE MAHABHARATA: THE POSSIBILITY THEREOF [Reprinted from Vishveshvaramand Indological Journal, Vol. XIV (1976) pp. 48-56.]

Hindus generally believe that the story of the Mahabharata (MBh.)1 [The references to MBh. given below are to its edition issued by Gopal Narayan and Co., Bombay, Saka 1823.] is a narrative of events that actually happened, and that they all took place near the end of the Dvaparayuga and the beginning of the Kaliyuga. Some hold that the War ended with the yuga and many, supported by the Puranas, say that Krsna passed away at the end of the yuga and so the War took place a few years earlier. About the question of the time when the Dvapara ended, there is difference of opinion. The popular view is that Dvapara ended and Kali began at the time fixed for it by the astronomical siddhantas, 3179 years before the Saka era of 78 A.D., which corresponds to Friday, 18th February, 3102 B.C., sunrise, or the previous midnight according to some schools.2 [Aryabhata does not give the exact time but merely states that 3600 years of Kali had ended when he was twenty- three years of age. But the followers of his school concur with the general astronomical tradition noticed above.] We do not know the exact grounds on which the siddhantins fixed the date as 3179 years before the saka era of 78 A.D. Most probably, the first siddhantins, like the author of the ‘Old’ Suryasiddhanta and Aryabhata, fixed the point of time as a convenient epoch, when the mean planets, according to them, coincided with the zero-point of the zodiac, and the later astronomers accepted it, and adjusted their own planetary cycles to agree with the epoch exactly, or nearly there, finding the difference to be small.

But there are other dates fixed for the end of Dvapara by people like Varahamihira, on the authority of the astronomical Samhitas and tradition current in their times. Varahamihira fixes the date as c. 2449 B C,, which can be known from his statement in his Brhatsamhita that the Saptarsis stood at Magha when Yudhisthira was ruling and that the year in his era can be got by adding 2526 to the years of the Saka era. The authority for this is Vrddha-Garga’s statement:

[x]

Kalhana, in his Rajatarangini, giving the chronology of the Kashmir kings in the Saptarsi or Laukika era current in Kashmir and the Himalayan regions, accepts Varahamihira’s view in toto, saying that people who fixed other dates were misguided:

[x]

The Jain tradition, giving 2634 B.C. for the Yudhisthira era is only a variation of Varahamihira’s view. The Saptarsicara of Parasara and the Aryasiddhanta of Aryabhata II, giving Magha for the sages in the seventh century of astronomical Kali, and the Matsyapurana, giving Krttika for the beginning of Kali, support Varahamihira.

But many think that both c. 3100 B.C. and c. 2450 or c. 2600 B.C. for the Bharata events are periods too early, considering the state of society and the political conditions depicted in the MBh. They try to fix the Kaliyuga epoch coupled with Yudhisthira’s rule, by reckoning backwards from the time of the Nanda dynasty, which historians have fixed at c. 400 B.C. onwards. The Visnupurana and the Bhagavata state:

[x]

Variants: (l) [x] (1510), (2) [x] (1015), (3) [x] (1500).

The above would mean that between Pariksit’s (grandson of the Pandavas) birth and Nanda’s coronation, the interval is 1053 years (variants: 1510, 1015, 1500). From this, they fix Pariksit’s time as c. 1500 B.C. (or 2000 B.C.) and thence the time of the Bharata story.

Besides these four main periods, several other periods are fixed based on various hypotheses, some plausible, some grotesque. For e.g., some scholars take the yuga measure of 12000 years as human years instead of divine, and fix a date accordingly. One interprets the word sama and varsa used in the Puranas as half-years and brings down the story to c. 1200 B.C. But few scholars make any clear distinction between the period of the ‘events’ and the period when they were written down in the form of the epic Mahabharata, while the orthodox traditional belief is that Vyasa, grandfather of the Pandavas and Kauravas, wrote the work, and his pupil Vaisampayana narrated it to King Janamejaya, grandson of the Pandavas.

Determining the period thus, each in his own way, these scholars try to fix the year and exact date of the war from the calendrical details and various astronomical phenomena mentioned in the context of the War, like certain planetary combinations, occurrences of eclipses etc. This is not an easy matter, because there is a lot of contradiction between various sets of planetary combinations themselves and among the other phenomena mentioned. Some of these passages may be set out here:

1. [x] (MBh., Bhisma, 3. 27)
2. [x] (Bhisma, 3. 18)
3. [x] (Salya, 11.17)
4. [x] (Bhisma, 3. 15)

Another gives:

5. [x](Karpa, 100. 17)
6. [x] (Bhisma, 3. 14)
7. [x] (Udyoga , 143. 8 - 9)

In the first set cited above (i.e., 1-4), we are told that Jupiter and Saturn are near the asterism Visakha. Mars is near Uttarasadha, Abhijit ( Brahmarasi ) and Sravana. In the second set, (5-7), Jupiter is said to be near Rohini. Mars is retrograde in Magha. Jupiter is in Sravana. (This contradicts two other statements.) Saturn is said to be in Purvaphalgunl. Saturn afflicts (?) Rohini. Mars is retrograde in Jyestha and is about to go to Anuradha. To add to the confusion, many people interpret the comets of different colours mentioned in Bhismaparva, chapter 3, as planets and, that too, each one differently.

Among the contradictory phenomena we can give the eclipses mentioned:

8. [x] (Bhisma, 3. 33)

Here a lunar eclipse, and next a solar eclipse are mentioned as having occurred before the war. Then, at the time of Duryodhana’s death the statement occurs:

[x] (S'alya, 27. 10)

mentioning another solar eclipse so near, when a lunar eclipse had occurred before the first solar eclipse.

Again, several impossible and some very rare phenomena, mentioned merely to indicate that these phenomena presage evil, are taken by many as having actually occurred, adding to the difficulty:

9. [x] (Mausala, Ch. 2)
[x] (Bhisma, 3. 3)
[x] (Udyoga, 143. l1)
[x] (Karna, 94. 51)
[x] (Bhisma, 2. 2)
[x] (Bhisma 3. 32)
[x] (S'alya, 27. 10)
[x] (Bhisma, 3.31)

Scholars trying to establish their conclusions interpret these verses differently, some neglecting one set and some another, some giving acceptable meanings and some far-fetched and extremely strained ones. A few examples will show to what extent these people go.3 [See K. L. Daftari, The astronomical method and its application to the chronology of ancient India, Nagpur University, 1941. See Lecture II. ‘The date of the Mahabharata war’, pp. 13-129.]

Passage 2, cited above, is interpreted thus: The planet Mars moved retrograde again and again, towards the constellation Sravana, and occupied the constellation of Brahma, i.e., Jupiter.4 [Op. cit., p. 27-28, art. 68.] The interpreter is unaware that Brahmarasi must mean ‘the group presided over by Brahma’, viz., Abhijit. He is unaware that anuvakra is a technical term used in astronomy and not 'again and again’. Passage 3 is interpreted thus: 'The planets Mars, Venus and Mercury were in front or to the east of the eldest of the sons of Pandu who were the masters of the whole land.5 [Op. cit., p. 28, art. 70. ] To the interpreter, caramam Panduputranam means Yudhisthira, being the last counted from the last of the sons of Pandu, while it means, simply, ‘behind the sons of Pandu and in front of the Kuru kings’. Line 9 of passage 9 is interpreted: The planet Mercury arose concealed, (invisibly).6 [Op. cit., p. 29, art. 72, 74.] The meaning ‘invisibly’ is given to tiras, not realising that anc with tiras means, only 'across or obliquely’. Passage 5 is interpreted: ‘Jupiter, having made Rohini to conceal herself (i.e., set), became like the sun or moon’.7 [Op. cit., p. 30, art. 76.] The passage means only that, Jupiter by his lustre hid Rohini. Passage 6 is interpreted: Mars is retrograde in Magha, and Jupiter in Sravana. Saturn is afflicting Purvaphalguni.8 [Op. cit., p. 31, art. 78.] In the next verse (not quoted here) there is the word sahita which this interpreter takes to mean ‘waiting’, and cites as an example the Raghuvamsa verse, dvitrany ahany arhasi sodhum arhan. In 9, line 8 is said to mean: ‘The lunar eciipse has already happened (in Karttika Purnima) and a solar eclipse is going to happen in the next Amavasya’.9 [Op, cit., p. 32, art. 81.] Actually, the first part means that the dark patch on the moon10 [For the meaning of laksma as ‘dark patch on the moon' cf. Kalidasa, malinam api himamsoh 'laksma’ laksmim tanot (Abhijnana Sakuntala, I, 20).] is inverted (vyavrttam, not nivrttam). In line 16 of passage 9, grdhra is interpreted as “an evil planet”, instead of ‘eagle’ which itself indicates an evil omen.

Thus, different years are fixed by different persons as follows:

N. Jagannatha Rao / 3139 B.C.
T.S. Narayana Sastri / c. 3126 B.C.
K.V. Abhayankar / c. 3101 B.C.
C.V. Vaidya / Do.
P.C. Sengupta / 2449 B.C.
Karandikar / 1931 B.C.
P.V. Kane / c. 1900 B.C.
S.B. Dikshit / c. 1500 B.C.
K.G. Sankara Aiyar / 1198 B.C.
K.L. Daftari / 1191 B.C.
V. Gopala Aiyar / 1194 B.C.

Within the year, the dates are fixed for the different occurrences by the day’s naksatra or tithi, and the interval in days between one occurrence and another, given. Here, too, there are discrepancies and misinterpretations, leading to different dates. Though many have concluded that the war began on Karttika New Moon day, some say that it began on Margasirsa Sukla Ekadasi day. The day of Bhisma’s death is stated at places as Magha Sukla Astami, while at others as Ekadasi. Cf.:

[x] (Udyoga , 80. 7)
[x]
[x](Udyoga, 143. 18)
[x] (S'alya, 5. 6)
[x] (Salya, 35. 10)
[x] (Bhisma, 20. 51-53)
[x] (Ib., 46. 29)
[x] (Ib., 47. 3)
[x] (Ib., 51. 10)
[x] (Anusasana, 167. 5)
[x] (Anusasana. 107. 5)

But most of the scholars do not seem to have gone to the heart of the matter, placing before themselves clearly the two things that have got to be investigated, viz: (1) How much of the Bharata story is true history, and when could it have happened. (2) When was it actually written down. Scholars who have studied the problem critically are of opinion that there is a historical core in the story, but much fictitious matter has been added to it in course of time. The Bharata war must be true history, and the personages taking part in it, together with the line of the Bharatas and Yadus, whose names occur frequently in Vedic literature, even as early as the Rgveda, not to speak of the Brahmanas like the Satapatha. The state of society and the political conditions point to a time earlier than the Chandogya, one of the earliest of the upanisads, as can be seen from two statements in the work:

[x]

The latter of the above statements shows that, at the time of the Upanisad, the Kuru and the Pancala country had coalesced, while at the time of the Bharata war they were different, the Pancalas being the allies of the Pandavas. It is quite natural for stories to gather accretions when they are repeated generation after generation. Most of the superhuman and obviously exaggerated portions must have been added later. The core is generally placed between the eleventh and the ninth centuries B.C. Other story matter could have been added during a few subsequent centuries, when Krsna came to be deified. The lot of Dharmasastra matter with the illustrative stories must have been added last, in the course of several generations. Anyhow, by the first or second century B.C. or A.D., the Mahabharata must have arrived at its present form, with a few bits of interpolations here and there, made later.

As for its writing, the language is that of the early classical period, for it is clearly later than that of the genuine upanisads. The addition of the later matter and the development of the classical language must have, naturally enough, gone on together. By the first or second century A.D. most of the whole Mahabharata must have attained the present form.

It is natural for story writers to incorporate into their stories ideas current in their own time. A lot of the astronomical facts found in the work, especially in the context of the war, must have been cooked up by these later writers in the light of their own knowledge, and added by different people at different times. That explains the contradictions. It must be clearly noted that the astrological ideas mentioned in the Samhitas which developed from the 2nd century B.C. could not have been current as early as the 11th to 9th century B.C. and, even if current, are not likely to be remembered after so many generations. By the first century A.D. or B.C., the astronomical Samhitas had mostly been written, and naturally the ideas in them find a place in the work. The Calendric system of the Vedanga Jyotisa continued to be current in this Samhita period, as can be seen from the Garga Samhita, and ideas showing Sravistha as being the first star (beginning the winter solstice) are in evidence, together with its shifting to Sravana, (c. third century B.C.) as can be gathered from the Visvamitra episode. The MBh. in its Virataparva ch. 52 contains the Vedanga calendric system.

Again, in the context of the war, it is natural for writers, especially of epics, to describe portents as happening to presage evil. The Samhitas devote chapters to describe these portents. The Ketucara, on the appearance of comets, is full of portents, as also separate chapters devoted to portents like rare or unnatural, impossible or terrible phenomena. These have been included in the work.11 [See, e.g., Udyoga, 143; Bhisma, 2, 3; Karna, 94, 100; S'alya, 11, 27; Mausala, 2.] But most investigators have not interpreted these portions properly, for which a detailed study of the chapters on Ketucara and Utpatas in the Brhatsamhita of Varahamihira would be advantageous. For example, the mention of the new moon together with solar eclipse occurring on Trayodasi, the sun and the moon being eclipsed on the same day (the same month), and that on Trayodasi, Mercury moving across the sky, (i.e., north-south), the dark patch on the moon being inverted, the lunar eclipse at Karttika full moon, the solar eclipse at Karttika new moon, and again the solar eclipse at the time of the mace-fight, are all intended by the writer to be impossible things occurring. The mention of the red moon indistinguishable from the red sky (digdaha), eagles falling on the flag, appearances of comets of different colours and in groups are all portents. Ignorance of the fact that the ‘grahas’ of different colours mentioned in Bhismaparva, chapter 3, are not planets but comets, has added to the confusion, because these scholars do not realise that, in the Samhitas, the word ‘graha’ means primarily comets, (vide the chapter on Ketucara in the Brhatsamhita).

It would be clear from the above, that all the skill shown in distorting the meanings of words and trying to show when these impossible or rare phenomena and contradictory planetary combinations would actually occur, has been wasted. Excepting the time of the year when the war might have happened, there is nothing in the Mahabharata to fix the year definitely. We do not have adequate data to fix either the happenings or when the work, even part by part, was written.

[admin]

Discourse X. Delivered February 28, 1793, P. 192, Excerpt from "Discourses Delivered Before the Asiatic Society: And Miscellaneous Papers, on The Religion, Poetry, Literature, Etc. of the Nations of India"
by Sir William Jones
1824
As. Res. vol. iv. p. 11, 1799

-- Discourses Delivered Before the Asiatic Society: And Miscellaneous Papers, on The Religion, Poetry, Literature, Etc. of the Nations of India, by Sir William Jones, 1824

Highlights:

Now the age of Vicramaditya is given; and if we can fix on an Indian prince contemporary with Seleucus, we shall have three given points in the line of time between Rama, or the first Indian colony, and Chandrabija, the last Hindu monarch who reigned in Bahar; so that only eight hundred or a thousand years will remain almost wholly dark; and they must have been employed in raising empires or states, in framing laws, improving languages and arts, and in observing the apparent motions of the celestial bodies. A Sanscrit [Sanskrit] history of the celebrated Vicramaditya was inspected at Benares by a Pandit, who would not have deceived me, and could not himself have been deceived; but the owner of the book is dead, and his family dispersed; nor have my friends in that city been able, with all their exertions, to procure a copy of it. ...

The jurisprudence of the Hindus and Arabs being the field which I have chosen for my peculiar toil, you cannot expect that I should greatly enlarge your collection of historical knowledge; but I may be able to offer you some occasional tribute; and I cannot help mentioning a discovery which accident threw in my way, though my proofs must be reserved for an essay which I have destined for the fourth volume of your Transactions. To fix the situation of that Palibothra (for there may have been several of the name) which was visited and described by Megasthenes, had always appeared a very difficult problem, for though it could not have been Prayaga, where no ancient metropolis ever stood, nor Canyacubja, which has no epithet at all resembling the word used by the Greeks; nor Gaur, otherwise called Lacshmanavati, which all know to be a town comparatively modern, yet we could not confidently decide that it was Pataliputra, though names and most circumstances nearly correspond, because that renowned capital extended from the confluence of the Sone and the Ganges to the site of Patna, while Palibothra stood at the junction of the Ganges and Erannoboas, which the accurate M. D'Anville had pronounced to be the Yamuna; but this only difficulty was removed, when I found in a classical Sanscrit book, near 2000 years old, that Hiranyabahu, or golden armed, which the Greeks changed into Erannoboas, or the river with a lovely murmur, was in fact another name for the Sona itself; though Megasthenes, from ignorance or inattention, has named them separately. This discovery led to another of greater moment, for Chandragupta, who, from a military adventurer, became like Sandracottus the sovereign of Upper Hindustan, actually fixed the seat of his empire at Pataliputra, where he received ambassadors from foreign princes; and was no other than that very Sandracottus who concluded a treaty with Seleucus Nicator; so that we have solved another problem, to which we before alluded, and may in round numbers consider the twelve and three hundredth years before Christ, as two certain epochs between Rama, who conquered Silan a few centuries after the flood, and Vicramaditya, who died at Ujjayini fifty-seven years before the beginning of our era.

Since these discussions would lead us too far, I proceed to the History of Nature...

But I should be led beyond the limits assigned to me on this occasion, if I were to expatiate farther on the historical division of the knowledge comprised in the literature of Asia; and I must postpone till next year my remarks on Asiatic Philosophy, and on those arts which depend on imagination; promising you with confidence, that in the course of the present year, your inquiries into the civil and natural history of this eastern world will be greatly promoted by the learned labours of many among our associates and correspondents.  

-- Discourse X. Delivered February 28, 1793, P. 192, Excerpt from "Discourses Delivered Before the Asiatic Society: And Miscellaneous Papers, on The Religion, Poetry, Literature, Etc. of the Nations of India", by Sir William Jones

ADVERTISEMENT.

The unfortunate Death of Sir William Jones, on the 27th April 1794, having deprived the Society of their Founder and President, a meeting of the Members was convened on the 1st May following, when it was unanimously agreed to appoint a Committee, consisting of Sir Robert Chambers, Mr. Justice Hyde, Colonel John Murray, John Bristow and Thomas Graham, Esqrs. to wait on Sir John Shore, and in the name of the Society, request his acceptance of the office of their President. With this request, he, in terms highly flattering to the Society, agreed to comply, and on the 22d May 1794, took his seat as President, and delivered the Discourse Number XII of this Volume.

EDMUND MORRIS, Secretary

***

I. The Tenth Anniversary Discourse, Delivered 28 February 1793 by The President on Asiatick History, Civil and Natural

Before our entrance into the Disquisition promised at the close of my Ninth Annual Discourse, on the particular Advantages which may be derived from our concurrent Researches in Asia, it seems necessary to fix with precision the sense in which we mean to speak of advantage or utility.....

-- Asiatick Researches: or, Transactions of the Society; Instituted in Bengal, For Inquiring Into The History and Antiquities, the Arts, Sciences, and Literature, of Asia, Volume IV, 1795

I thought also that it would not be useless to reduce the Astronomy of Europe to this form, to be able to supply the want of the Tables which greatly abridge the work. This method would be much more easie to practice in the form of the Julian and Gregorian year of which we make use, than in the form of the Lunisolar year, which the Orientals observe: for their principal difficulty consists in reducing the Lunisolar years and the Civil Lunary months to the years and months of the Sun, which the form of our Kalender immediately gives us; and what has given me the most trouble, has been to find out the method which they use to reduce them, in which the several sorts of Years, Months and Days, which are supposed and sought, are not distinguished. Wherefore the reason of the Explication which I give, and of the Determination of the Genus to the Species which I make in the beginning, will not presently be understood; but in the sequel it will be comprehended by the Connexion of things, and by what necessarily results therefrom.

-- Rules of the Siamese Astronomy, for calculating the Motions of the Sun and Moon, translated from the Siamese, and since examined and explained by M. Cassini, a Member of the Royal Academy of Sciences, Excerpt from "A New Historical Relation of the Kingdom of Siam", Tome II, by Monsieur De La Loubere

Discourse X. Delivered February 28, 1793

On Asiatic History, Civil and Natural.

Introductory remarks. -- The Mosaic account of the primitive world confirmed. -- The practical use of history. -- Observations on animals, minerals, and vegetable substances. -- On the mechanical arts, &c.

GENTLEMEN,

Before our entrance into the Disquisition promised at the close of my Ninth Annual Discourse, on the particular Advantages which may be derived from our concurrent Researches in Asia, it seems necessary to fix with precision the sense in which we mean to speak of advantage or utility. Now, as we have described the five Asiatic regions on their largest scale, and have expanded our conceptions in proportion to the magnitude of that wide field, we should use those words which comprehend the fruit of all our inquiries, in their most extensive acceptation; including not only the solid conveniences and comforts of social life, but its elegances and innocent pleasures, and even the gratification of a natural and laudable curiosity; for, though labour be clearly the lot of man in this world, yet, in the midst of his most active exertions, he cannot but feel the substantial benefit of every liberal amusement which may lull his passions to rest, and afford him a sort of repose, without the pain of total inaction, and the real usefulness of every pursuit which may enlarge and diversity his ideas, without interfering with the principal objects of his civil station or economical duties; nor should we wholly exclude even the trivial and worldly sense of utility, which too many consider as merely synonymous with lucre, but should reckon among useful objects those practical, and by no means illiberal arts, which may eventually conduce both to national and to private emolument. With a view then to advantages thus explained, let us examine every point in the whole circle of arts and sciences, according to the received order of their dependence on the faculties of the mind, their mutual connexion, and the different subjects with which they are conversant: our inquiries indeed, of which Nature and Man are the primary objects, must of course be chiefly historical; but since we propose to investigate the actions of the several Asiatic nations, together with their respective progress in science and art, we may arrange our investigations under the same three heads to which our European analysis have ingeniously reduced all the branches of human knowledge: and my present Address to the Society shall be confined to History, civil and natural, or the observation and remembrance of mere facts, independently of ratiocinatios, which belongs to philosophy; or of imitations and substitutions, which are the province of art.

"The ambiguous expression reliqua Seleuco Nicatori peragrata sunt, translated above as 'the other journeys made, for Seleukos Nikator,' according to Schwanbeck's opinion, contain a dative 'of advantage,' and therefore can bear no other meaning. The reference is to the journeys of Megasthenes, Deimachos, and Patrokles, whom Seleukos had sent to explore the more remote regions of Asia. Nor is the statement of Plinius in a passage before this more distinct. ('India,') he says, 'was thrown open not only by the arms of Alexander the Great, and the kings who were his successors, of whom Seleucus and Antiochus even travelled to the Hyrcanian and Caspian seas, Patrocles being commander of their fleet, but all the Greek writers who stayed behind with the Indian kings (for instance, Megasthenes, and Dionysius, sent by Philadelphus for that purpose) have given accounts of the military force of each nation.' Schwanbeck thinks that the words circumsectis etiam ... Seleuco et Antiocho et Patrocle are properly meant to convey nothing but additional confirmation, and also an explanation how India was opened up by the arms of the kings who succeeded Alexander."

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle, M.A., Principal of the Government College, Patna, Member of the General Council of the University of Edinburgh, Fellow of the University of Calcutta, With Introduction, Notes and Map of Ancient India

Were a superior created intelligence to delineate a map of general knowledge (exclusively of that sublime and stupendous theology, which himself could only hope humbly to know by an infinite approximation) he would probably begin by tracing with Newton the system of the universe, in which he would assign the true place to our little globe; and having enumerated its various inhabitants, contents, and productions, would proceed to man in his natural station among animals, exhibiting a detail of all the knowledge attained or attainable by the human race; and thus observing perhaps the same order in which he had before described other beings in other inhabited worlds; but though Bacon seems to have had a similar reason for placing the History of Nature before that of Man, or the whole before one of its parts, yet, consistently with our chief object already mentioned, we may properly begin with the Civil History of the Five Asiatic Nations, which necessarily comprises their geography, or a description of the places where they have acted, and their astronomy, which may enable us to fix with some accuracy the time of their actions: we shall thence be led to the history of such other animals, of such minerals, and of such vegetables, as they may be supposed to have found in their several migrations and settlements, and shall end with the uses to which they have applied, or may apply, the rich assemblage of natural substances.

I. In the first place, we cannot surely deem it an inconsiderable advantage that all our historical researches have confirmed the Mosaic accounts of the primitive world; and our testimony on that subject ought to have the greater weight, because, if the result of our observations had been totally different, we should nevertheless have published them, not indeed with equal pleasure, but with equal confidence; for truth is mighty, and, whatever be its consequences, must always prevail; but, independently of our interest in corroborating the multiplied evidences of revealed religion, we could scarce gratify our minds with a more useful and rational entertainment than the contemplation of those wonderful revolutions in kingdoms and states which have happened within little more than four thousand years; revolutions, almost as fully demonstrative of an all-ruling Providence, as the structure of the universe, and the final causes which are discernible in its whole extent, and even in its minutest parts. Figure to your imaginations a moving picture of that eventful period, or rather, a succession of crowded scenes rapidly changed. Three families migrate in different courses from one region, and, in about four centuries, establish very distant governments and various modes of society: Egyptians, Indians, Goths, Phenicians, Celts, Greeks, Latians, Chinese, Peruvians, Mexicans, all sprung from the same immediate stem , appear to start nearly at one time, and occupy at length those countries, to which they have given, or from which they have derived their names. In twelve or thirteen hundred years more, the Greeks overrun the land of their forefathers, invade India, conquer Egypt, and aim at universal dominion; but the Romans appropriate to themselves the whole empire of Greece, and carry their arms into Britain, of which they speak with haughty contempt. The Goths, in the fulness of time, break to pieces the unwieldy Colossus of Roman power, and seize on the whole of Britain, except its wild mountains; but even those wilds become subject to other invaders, of the same Gothic lineage. During all those transactions, the Arabs possess both coasts of the Red Sea, subdue the old seat of their first progenitors, and extend their conquests, on one side through Africa, into Europe itself; on another, beyond the borders of India, part of which they annex to their flourishing empire. In the same interval the Tartars, widely diffused over the rest of the globe, swarm in the north-east, whence they rush to complete the redaction of Constantine's beautiful domains, to subjugate China, to raise in these Indian realms a dynasty splendid and powerful, and to ravage, like the two other families, the devoted regions of Iran. By this time the Mexicans and Peruvians with many races of adventurers variously intermixed, have peopled the continent and isles of America, which the Spaniards, having restored their old government in Europe, discover, and in part overcome: but a colony from Britain, of which Cicero ignorantly declared that it contained nothing valuable, obtain the possession, and finally the sovereign dominion, of extensive American districts; whilst other British subjects acquire a subordinate empire in the finest provinces of India, which the victorious troops of Alexander were unwilling to attack. This outline of human transactions, as far as it includes the limits of Asia, we can only hope to fill up, to strengthen, and to colour, by the help of Asiatic literature; for in history, as in law, we must not follow streams when we may investigate fountains, nor admit any secondary proof where primary evidence is attainable: I should nevertheless make a bad return for your indulgent attention, were I to repeat a dry list of all the Musselman historians whose works are preserved in Arabic, Persian, and Turkish, or expatiate on the histories and medals of China and Japan, which may in time be accessible to Members of our Society, and from which alone we can expect information concerning the ancient state of the Tartars; but on the history of India, which we naturally consider as the centre of our inquiries, it may not be superfluous to present you with a few particular observations.

Our knowledge of Civil Asiatic History (I always except that of the Hebrews) exhibits a short evening twilight in the venerable introduction to the first book of Moses, followed by a gloomy night, in which different watches are faintly discernible, and at length we see a dawn succeeded by a sunrise more or less early, according to the diversity of regions. That no Hindu nation but the Cashmirians, have left us regular histories in their ancient language, we must ever lament; but from the Sanscrit [Sanskrit] literature, which our country has the honour of having unveiled, we may still collect some rays of historical truth, though time and a series of revolutions have obscured that light which we might reasonably have expected from so diligent and ingenious a people. The numerous Puranas and Itihasas, or poems mythological and heroic, are completely in our powers and from them we may recover some disfigured but valuable pictures of ancient manners and governments; while the popular tales of the Hindus, in prose and in verse, contain fragments of history; and even in their dramas we may find as many real characters and events as a future age might find in our own plays, if all histories of England were, like those of India, to be irrecoverably lost. For example: A most beautiful poem by Somadeva, comprising a very long chain of instinctive and agreeable stories, begins with the famed revolution at Pataliputra, by the murder of king Nanda with his eight sons, and the usurpation of Chandragupta;

Somadeva was an 11th century CE writer from Kashmir. He was the author of a famous compendium of Indian legends, fairy tales and folk tales - the Kathasaritsagara.

The Kathāsaritsāgara ("Ocean of the Streams of Stories") is a famous 11th-century collection of Indian legends, fairy tales and folk tales as retold in Sanskrit by the Shaivite Somadeva.

Kathāsaritsāgara contains multiple layers of story within a story and is said to have been adopted from Guṇāḍhya's Bṛhatkathā, which was written in a poorly-understood language known as Paiśācī.

The work is no longer extant but several later adaptations still exist — the Kathāsaritsāgara, Bṛhatkathamanjari and Bṛhatkathāślokasaṃgraha. However, none of these recensions necessarily derives directly from Gunadhya, and each may have intermediate versions. Scholars compare Guṇāḍhya with Vyasa and Valmiki even though he did not write the now long-lost Bṛhatkathā in Sanskrit. Presently available are its two Sanskrit recensions, the Bṛhatkathamanjari by Kṣemendra and the Kathāsaritsāgara by Somadeva.

-- Kathasaritsagara, by Wikipedia

Guṇāḍhya is the Sanskrit name of the sixth-century Indian author of the Bṛhatkathā, a large collection of tales attested [attest: declare that something exists or is the case; be a witness to; certify formally] by Daṇḍin, the author of the Kavyadarsha, Subandhu, the author of Vasavadatta, and Bāṇabhaṭṭa, the author of the Kadambari. Scholars compare Guṇāḍhya with Vyasa and Valmiki even though he did not write the now long-lost Brihatkatha in Sanskrit; the loss of this text is one of the greatest losses of Indian literature. Presently available are its two Kashmiri Sanskrit recensions, the Brihatkathamanjari by Kshemendra and the Kathasaritsagara by Somadeva.

-- Gunadhya, by Wikipedia

Not much is known about him except that his father's name was Rama and he composed his work (probably during the years 1063-81 CE) for the entertainment of the queen Suryamati, a princess of Jalandhara and wife of King Ananta of Kashmir. The queen was quite distraught as it was a time when the political situation in Kashmir was 'one of discontent, intrigue, bloodshed and despair'.

-- Somadeva, by Wikipedia

and the same revolution is the subject of a tragedy in Sanscrit [Sanskrit], entitled, the Coronation of Chandra, the abbreviated name of that able and adventurous usurper.

"Vijaka wrote Kaumudi Mahotsava to commemorate the coronation of Chandra Gupta I [319-335 or 319-350 CE]. The play has some historical value." (Winternitz)

-- Indian Civilization & Culture, by Suhas Chatterjee

From these once concealed, but now accessible, compositions, we are enabled to exhibit a more accurate sketch of old Indian history than the world has yet seen, especially with the aid of well attested observations on the places of the colures.

The following passage of the Indian comedy Mudrarakshasa seems to favour the Indian expedition: — "Meanwhile Kusmuapura (i.e. Pataliputra, Palimbothra) the city of Chandragupta and the king of the mountain regions, was invested on every side, by the Kiratas, Yavanas, Kambojas, Persians, Baktrians, and the rest." But "that drama" (Schwanbeck, p. 18), "to follow the authority of Wilson, was written in the tenth century after Christ,— certainly ten centuries after Seleukos. When even the Indian historians have no authority in history, what proof can dramas give written after many centuries?

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle

Amongst Sanskrit plays, the historical play Mudrarakshasa is unique because it contains political intrigue and is full of life, action and sustained interest. The time period of composition is prior to 800 C.E. In the play, Chandragupta Maurya is ruling from Pataliputra, having deposed the last of the Nanda kings. Rakshasa the minister of Nanda, attempts to avenge his late master. Chanakya, the minister of Chandragupta succeeds in winning over Rakshasa to his master's side.

-- Mudrarakshasa of Vishakhadatta, by Wikipedia

It is now clearly proved, that the first Purana contains an account of the deluge; between which and the Mohammedan conquests the history of genuine Hindu government must of course be comprehended: but we know from an arrangement of the seasons in the astronomical work of Parasara, that the war of the Pandavas could not have happened earlier than the close of the twelfth century before Christ; and Seleucus most therefore have reigned about nine centuries after that war. Now the age of Vicramaditya is given; and if we can fix on an Indian prince contemporary with Seleucus, we shall have three given points in the line of time between Rama, or the first Indian colony, and Chandrabija, the last Hindu monarch who reigned in Bahar; so that only eight hundred or a thousand years will remain almost wholly dark; and they must have been employed in raising empires or states, in framing laws, improving languages and arts, and in observing the apparent motions of the celestial bodies. A Sanscrit [Sanskrit] history of the celebrated Vicramaditya was inspected at Benares by a Pandit, who would not have deceived me, and could not himself have been deceived; but the owner of the book is dead, and his family dispersed; nor have my friends in that city been able, with all their exertions, to procure a copy of it. As to the Mogul conquests, with which modern Indian history begins, we have ample accounts of them in Persian, from Ali of Yezd, and the translations of Turkish books composed even by some of the conquerors, to Ghulam Husain, whom many of us personally know, and whose impartiality deserves the highest applause, though his unrewarded merit will give no encouragement to other contemporary historians, who, to use his own phrase in a letter to myself, may, like him, consider plain truth as the beauty of historical composition. From all these materials, and from these alone, a perfect history of India (if a mere compilation however elegant, could deserve such a title) might be collected by any studious man who had a competent knowledge of Sanscrit [Sanskrit], Persian, and Arabic; but even in the work of a writer so qualified, we could only give absolute credence to the general outline; for, while the abstract sciences are all truth, and the fine arts all fiction, we cannot but own, that in the details of history, truth and fiction are so blended as to be scarce distinguishable.

The practical use of history, in affording particular examples of civil and military wisdom, has been greatly exaggerated; but principles of action may certainly be collected from it; and even the narrative of wars and revolutions may serve as a lesson to nations, and an admonition to sovereigns. A desire indeed of knowing past events, while the future cannot be known, and a view of the present gives often more pain than delight, seems natural to the human mind: and a happy propensity would it be if every reader of history would open his eyes to some very important corollaries, which flow from the whole extent of it. He could not but remark the constant effect of despotism in benumbing and debasing all those faculties which distinguish men from the herd that grazes; and to that cause he would impute the decided inferiority of most Asiatic nations, ancient and modern, to those in Europe who are blessed with happier governments; he would see the Arabs rising to glory while they adhered to the free maxims of their bold ancestors, and sinking to misery from the moment when those maxims were abandoned. On the other hand, he would observe with regret, that such republican governments as tend to produce virtue and happiness, cannot in their nature be permanent, but are generally succeeded by oligarchies which no good man would wish to be durable. He would then, like the king of Lydia, remember Solon, the wisest, bravest, and most accomplished of men, who asserts in four nervous lines, that "as hail and snow which mar the labours of husbandmen, proceed from elevated clouds, and, as the destructive thunderbolt follows the brilliant flash; thus is a free state ruined by men exalted in power and splendid in wealth; while the people, from gross ignorance, choose rather to become the slaves of one tyrant, that they may escape from the domination of many, than to preserve themselves from tyranny of any kind by their union and their virtues." Since, therefore, no unmixed form of government could both deserve permanence and enjoy it, and since changes, even from the worst to the best are always attended with much temporary mischief, he would fix on our British constitution (I mean our public law, not the actual state of things in any given period) as the best form ever established, though we can only make distant approaches to its theoretical perfection. In these Indian territories, which Providence has thrown into the arms of Britain for their protection and welfare, the religion, manners, and laws of the natives preclude even the idea of political freedom; but their histories may possibly suggest hints for their prosperity, while our country derives essential benefit from the diligence of a placid and submissive people, who multiply with such increase, even after the ravages of famine, that in one collectorship out of twenty-four, and that by no means the largest or best cultivated (I mean Crishna-nagar) there have lately been found, by an actual enumeration, a million and three hundred thousand native inhabitants; whence it should seem, that in all India there cannot he fewer than thirty millions of black British subjects.

Let us proceed to geography and chronology, without which history would be no certain guide, but would resemble a kindled vapour without either a settled place or a steady light. For a reason before intimated, I shall not name the various cosmographical books which are extant in Arabic and Persian, nor give an account of those which the Turks have beautifully printed in their own improved language, but shall expatiate a little on the geography and astronomy of India; having first observed generally, that all the Asiatic nations must be far better acquainted with their several countries than mere European scholars and travellers; that consequently, we must learn their geography from their own writings: and that by collating many copies of the same work, we may correct blunders of transcribers in tables, names, and descriptions.

Geography, astronomy, and chronology have, in this part of Asia, shared the fate of authentic history; and, like that, have been so masked and bedecked in the fantastic robes of mythology and metaphor, that the real system of Indian philosophers and mathematicians can scarce be distinguished: an accurate knowledge of Sanscrit [Sanskrit], and a confidential intercourse with learned Brahmens, are the only means of separating truth from fable; and we may expect the most important discoveries from two of our members, concerning whom it may be safely asserted, that if our Society should have produced no other advantage than the invitation given to them for the public display of their talents, we should have a claim to the thanks of our country and of all Europe. Lieutenant Wilford has exhibited an interesting specimen of the geographical knowledge deducible from the Puranas, and will in time present you with so complete a treatise on the ancient world known to the Hindus, that the light acquired by the Greeks will appear but a glimmering in comparison of that he will diffuse; while Mr. Davis, who has given us a distinct idea of Indian computations and cycles, and ascertained the place of the colures at a time of great importance in history, will hereafter disclose the systems of Hindu astronomers, from Nared and Parasar to Meya, Varahamihir, and Bhascar; and will soon, I trust, lay before you a perfect delineation of all the Indian asterisms in both hemispheres, where you will perceive so strong a general resemblance to the constellations of the Greeks, as to prove that the two systems were originally one and the same, yet with such a diversity in parts, as to show incontestibly that neither system was copied from the other; whence it will follow, that they must have had some common source.

The jurisprudence of the Hindus and Arabs being the field which I have chosen for my peculiar toil, you cannot expect that I should greatly enlarge your collection of historical knowledge; but I may be able to offer you some occasional tribute; and I cannot help mentioning a discovery which accident threw in my way, though my proofs must be reserved for an essay which I have destined for the fourth volume of your Transactions. To fix the situation of that Palibothra (for there may have been several of the name) which was visited and described by Megasthenes, had always appeared a very difficult problem, for though it could not have been Prayaga, where no ancient metropolis ever stood, nor Canyacubja, which has no epithet at all resembling the word used by the Greeks; nor Gaur, otherwise called Lacshmanavati, which all know to be a town comparatively modern, yet we could not confidently decide that it was Pataliputra, though names and most circumstances nearly correspond, because that renowned capital extended from the confluence of the Sone and the Ganges to the site of Patna, while Palibothra stood at the junction of the Ganges and Erannoboas, which the accurate M. D'Ancille had pronounced to be the Yamuna; but this only difficulty was removed, when I found in a classical Sanscrit [Sanskrit] book, near 2000 years old, that Hiranyabahu, or golden armed, which the Greeks changed into Erannoboas, or the river with a lovely murmur, was in fact another name for the Sona itself; though Megasthenes, from ignorance or inattention, has named them separately. This discovery led to another of greater moment, for Chandragupta, who, from a military adventurer, became like Sandracottus the sovereign of Upper Hindustan, actually fixed the seat of his empire at Pataliputra, where he received ambassadors from foreign princes; and was no other than that very Sandracottus who concluded a treaty with Seleucus Nicator; so that we have solved another problem, to which we before alluded, and may in round numbers consider the twelve and three hundredth years before Christ, as two certain epochs between Rama, who conquered Silan a few centuries after the flood, and Vicramaditya, who died at Ujjayini fifty-seven years before the beginning of our era.

Partly from curiosity and partly from idleness, I went into the lecturing room, which M. Waldman entered shortly after. This professor was very unlike his colleague. He appeared about fifty years of age, but with an aspect expressive of the greatest benevolence; a few grey hairs covered his temples, but those at the back of his head were nearly black. His person was short but remarkably erect and his voice the sweetest I had ever heard. He began his lecture by a recapitulation of the history of chemistry and the various improvements made by different men of learning, pronouncing with fervour the names of the most distinguished discoverers. He then took a cursory view of the present state of the science and explained many of its elementary terms. After having made a few preparatory experiments, he concluded with a panegyric upon modern chemistry, the terms of which I shall never forget: "The ancient teachers of this science," said he, "promised impossibilities and performed nothing. The modern masters promise very little; they know that metals cannot be transmuted and that the elixir of life is a chimera but these philosophers, whose hands seem only made to dabble in dirt, and their eyes to pore over the microscope or crucible, have indeed performed miracles. They penetrate into the recesses of nature and show how she works in her hiding-places. They ascend into the heavens; they have discovered how the blood circulates, and the nature of the air we breathe. They have acquired new and almost unlimited powers; they can command the thunders of heaven, mimic the earthquake, and even mock the invisible world with its own shadows."

Such were the professor's words—rather let me say such the words of the fate—enounced to destroy me. As he went on I felt as if my soul were grappling with a palpable enemy; one by one the various keys were touched which formed the mechanism of my being; chord after chord was sounded, and soon my mind was filled with one thought, one conception, one purpose. So much has been done, exclaimed the soul of Frankenstein—more, far more, will I achieve; treading in the steps already marked, I will pioneer a new way, explore unknown powers, and unfold to the world the deepest mysteries of creation.

-- Frankenstein Or, The Modern Prometheus, by Mary Wollstonecraft (Godwin) Shelley

II. Since these discussions would lead us too far, I proceed to the History of Nature, distinguished, for our present purpose, from that of Man; and divided into that of other animals who inhabit this globe, of the mineral substances which it contains, and of the vegetables which so luxuriantly and so beautifully adorn it.

1. Could the figure, instincts, and qualities of birds, beasts, insects, reptiles, and fishes, be ascertained, either on the plan of Buffon, or on that of Linnaeus, without giving pain to the objects of our examination, few studies would afford us more solid instruction, or more exquisite delight; but I never could learn by what right, nor conceive with what feelings, a naturalist can occasion the misery of an innocent bird, and leave its young perhaps to perish in a cold nest, because it has gay plumage, and has never been accurately delineated; or deprive even a butterfly of its natural enjoyments, because it has the misfortune to be rare or beautiful; nor shall I ever forget the couplet of Firdausi, for which Sadi, who cites it with applause, pours blessings on his departed spirit: —

Ah! spare yon emmet, rich in hoarded grain;
tie lives with pleasure, and he dies with pain.

This may be only a confession of weakness, and it certainly is not meant as a boast of peculiar sensibility; but whatever name may be given to my opinion, it has such an effect on my conduct, that I never would suffer the Cocila, whose wild native woodnotes announce the approach of spring, to be caught in my garden, for the sake of comparing it with Buffon's description; though I have often examined the domestic and engaging Mayana, which bids us good morrow at our windows, and expects as its reward little more than security: even when a fine young Manis or Pangolin was brought me against my wish from the mountains, I solicited his restoration to his beloved rocks, because I found it impossible to preserve him in comfort at a distance from them. There are several treatises on Animals in Arabia, and very particular accounts of them in Chinese, with elegant outlines of their external appearance; but I met with nothing valuable concerning them in Persian, except what may be gleaned from the medical dictionaries; nor have I yet seen a book in Sanscrit [Sanskrit] that expressly treats of them. On the whole, though rare animals may be found in all Asia, yet I can only recommend an examination of them with this condition, that they be left as much as possible in a state of natural freedom; or made as happy as possible, if it be necessary to keep them confined.

2. The History of Minerals, to which no such objection can be made, is extremely simple and easy, if we merely consider their exterior look and configuration, and their visible texture; but the analysis of their internal properties belongs particularly to the sublime researches of Chemistry, on which we may hope to find useful disquisitions in Sanscrit [Sanskrit], since the old Hindus unquestionably applied themselves to that enchanting study; and even from their treatises on alchymy we may possibly collect the results of actual experiment, as their ancient astrological works have preserved many valuable facts relating to the Indian sphere, and the procession of the equinox. Both in Persian and Sanscrit [Sanskrit] there are books on metals and minerals, particularly on gems, which the Hindu philosophers considered (with an exception of the diamond) as varieties of one crystalline substance, either simple or compound: but we must not expect from the chemists of Asia those beautiful examples of analysis which have but lately been displayed in the laboratories of Europe.

3. We now come to Botany, the loveliest and most copious division in the history of nature; and all disputes on the comparative merit of systems being at length, I hope, condemned to one perpetual night of undisturbed slumber, we cannot employ our leisure more delightfully than in describing all new Asiatic plants in the Linnaean style and method, or in correcting the descriptions of those already known, but of which dry specimens only, or drawings, can have been seen by most European botanists. In this part of natural history, we have an ample field yet unexplored; for, though many plants of Arabia have been made known by Garcias, Prosper Alpinus, and Forskoel; of Persia, by Garcin; of Tartary, by Gmelin and Pallas; of China and Japan, by Koempfer, Osbeck, and Thunberg; of India, by Rheede and Rumphias, the two Burmans, and the much lamented Koenig, yet none of those naturalists were deeply versed in the literature of the several countries from which their vegetable treasures had been procured; and the numerous works in Sanscrit [Sanskrit] on medical substances, and chiefly on plants, have never been inspected, or never at least understood, by any European attached to the study of nature. Until the garden of the India Company shall be fully stored (as it will be, no doubt, in due time) with Arabian, Persian, and Chinese plants, we may well be satisfied with examining the native flowers of our own provinces; but unless we can discover the Sanscrit [Sanskrit] names of all celebrated vegetables, we shall neither comprehend the allusions which Indian Poets perpetually make to them, nor (what is far worse) be able to find accounts of their tried virtues in the writings of Indian physicians; and (what is worst of all) we shall miss an opportunity which never again may present itself; for the Pandits themselves have almost wholly forgotten their ancient appellations of particular plants; and, with all my pains, I have not yet ascertained more than two hundred out of twice that number, which are named in their medical or poetical compositions. It is much to be deplored, that the illustrious Van Rheede had no acquaintance with Sanscrit [Sanskrit], which even his three Brahmens, who composed the short preface engraved in that language, appear to have understood very imperfectly, and certainly wrote with disgraceful inaccuracy. In all his twelve volumes, I recollect only Bunarnava, in which the Nagari letters are tolerably right; the Hindu words in Arabian characters are shamefully incorrect; and the Malabar, I am credibly informed, is as bad as the rest. His delineations, indeed, are in general excellent; and though Linnaeus himself could not extract from his written descriptions the natural character of every plant in the collection, yet we shall be able, I hope, to describe them all from the life, and to add a considerable number of new species, if not of new genera, which Rheede, with all his noble exertions, could never procure. Such of our learned members as profess medicine, will no doubt cheerfully assist in these researches, either by their own observations, when they have leisure to make any, or by communications from other observers among their acquaintance, who may reside in different parts of the country: and the mention of their art leads me to the various uses of natural substances, in the three kingdoms or classes to which they are generally reduced.

III. You cannot but have remarked, that almost all the sciences, as the French call them, which are distinguished by Greek names, and arranged under the head of Philosophy, belong for the most part to History; such as philology, chemistry, physic, anatomy, and even metaphysics, when we barely relate the phenomena of the human mind; for, in all branches of knowledge, we are only historians when we announce facts; and philosophers only when we reason on them: the same may be confidently said of law and of medicine, the first of which belongs principally to Civil, and the second chiefly to Natural History. Here, therefore, I speak of medicine, as far only as it is grounded on experiment; and, without believing implicitly what Arabs, Persians, Chinese, or Hindus may have written on the virtues of medicinal subjects, we may surely hope to find in their writings what our own experiments may confirm or disprove, and what might never have occurred to us without such intimations.

Europeans enumerate more than two hundred and fifty mechanical arts, by which the productions of nature may be variously prepared for the convenience and ornament of life; and though the Silpasastra reduces them to sixty-four, yet Abulfazl had been assured that the Hindus reckoned three hundred arts and sciences; now, their sciences being comparatively few, we may conclude that they anciently practised at least as many useful arts as ourselves. Several Pandits have informed me, that the treatises on art, which they call Upavedas, and believe to have been inspired, are not so entirely lost but that considerable fragments of them may be found at Benares; and they certainly possess many popular, but ancient works on that interesting subject. The manufactures of sugar and indigo have been well known in these provinces for more than two thousand years; and we cannot entertain a doubt that their Sanscrit [Sanskrit]books on dying and metallurgy, contain very curious facts, which might indeed be discovered by accident in a long course of years, but which we may soon bring to light by the help of Indian literature, for the benefit of manufactures and artists, and consequently of our nation, who are interested in their prosperity. Discoveries of the same kind might be collected from the writings of other Asiatic nations, especially of the Chinese; but, though Persian, Arabic, Turkish, and Sanscrit [Sanskrit] are languages now so accessible, that in order to attain a sufficient knowledge of them, little more seems required than a strong inclination to learn them, yet the supposed number and intricacy of the Chinese characters have deterred our most diligent students from attempting to find their way through so vast a labyrinth. It is certain, however, that the difficulty has been magnified beyond the truth; for the perspicuous g rammar of M. Fourmont, together with a copious dictionary, which I possess in Chinese and Latin, would enable any man who pleased, to compare the original works of Confucius, which are easily procured, with the literal translation of them by Couplet; and having made that first step with attention, he would probably find that he had traversed at least half of his career. But I should be led beyond the limits assigned to me on this occasion, if I were to expatiate farther on the historical division of the knowledge comprised in the literature of Asia; and I must postpone till next year my remarks on Asiatic Philosophy, and on those arts which depend on imagination; promising you with confidence, that in the course of the present year, your inquiries into the civil and natural history of this eastern world will be greatly promoted by the learned labours of many among our associates and correspondents.  

[admin]

Bias in Ptolemy's History of Alexander1 [An early version of this paper was read to the meeting of Hibernian Hellenists at Ballymascanlon in March 1968. I am grateful for comments made then, and to Professor E. Badian for reading a subsequent draft.]
by R. M. Errington
The Queen's University, Belfast
The Classical Quarterly
Vol. 19, No. 2, pp. 233-242 (10 pages)
Published by: Cambridge University Press on behalf of The Classical Association
Nov., 1969

NOTICE: THIS WORK MAY BE PROTECTED BY COPYRIGHT

YOU ARE REQUIRED TO READ THE COPYRIGHT NOTICE AT THIS LINK BEFORE YOU READ THE FOLLOWING WORK, THAT IS AVAILABLE SOLELY FOR PRIVATE STUDY, SCHOLARSHIP OR RESEARCH PURSUANT TO 17 U.S.C. SECTION 107 AND 108. IN THE EVENT THAT THE LIBRARY DETERMINES THAT UNLAWFUL COPYING OF THIS WORK HAS OCCURRED, THE LIBRARY HAS THE RIGHT TO BLOCK THE I.P. ADDRESS AT WHICH THE UNLAWFUL COPYING APPEARED TO HAVE OCCURRED. THANK YOU FOR RESPECTING THE RIGHTS OF COPYRIGHT OWNERS.

-- Errors in Arrian, by A. B. Bosworth

Arrian's enthusiasm for Ptolemy's account of Alexander has often been echoed in modern times.2 [A(rrian) I. I (all references are to the Anabasis unless otherwise stated). Cf. W. W. Tarn, Alexander the Great (Cambridge, 1949), passim: L. Pearson, The Lost Histories of Alexander the Great (New York, (1960), esp. 188 ff.] With much justification it is generally agreed that Arrian's account of Alexander, through its reliance on the works of Ptolemy and Aristobulus, is our best and, on the whole, most reliable account of Alexander. Recent work, however, has illuminated Ptolemy's weaknesses, and we can no longer regard Ptolemy as utterly reliable in every important respect.3 [See especially the articles of E. Badian in TAPhA, 1960, Historia, 1958, C.Q., 1958. Also his comments on Pearson's book in Gnomon, 1961 (reprinted in Studies in Greek and Roman History [Oxford, 1964], 250 ff.); C. B. Welles, Miscellanea Rostagni (Turin, 1963), 101 ff.] His version of the Alexander story is centred on Alexander, therefore Alexander is depicted out of the close context of the Macedonian court.4 [Clearly shown by H. Strasburger, Ptolemaios und Alexander (Leipzig, 1934), 50 ff.] It is only through the information preserved in other writers -- traditionally, but undiscriminatingly, considered unreliable -- that, for instance, the picture of Alexander's struggle with his Macedonian nobles has begun to emerge. And in matters of this kind Ptolemy's version is so much the court 'official' version that it cannot be regarded as trustworthy.

From these studies a new dimension has been revealed in Ptolemy's history. Far from being a simple military narrative, a general's story, 'to set the record straight',5 [So Pearson, Lost Histories, 193 ff. (with bibliography).] it is as much a political history as any, even if much of the distortion is caused by omitting crucial events. Strasburger in 1934 noted Ptolemy's penchant for throwing Alexander's activities into relief by omitting details about his nobles', except in purely military contexts where mention was unavoidable.6 [Potlemaios und Alexander, 50 ff.] Strasburger attributed Ptolemy's unwillingness to allow too much success to Alexander's nobles, and his complementary emphasis on Alexander's own activities, to Ptolemy's loyalist point of view, and he did not regard it as being of any great importance. But Badian's more recent work has shown that, far from being unimportant, it is one of the most unsatisfactory aspects of Ptolemy's historical work.

Welles has tried to plot another aspect of Ptolemy's bias:7 [Miscellanea Rostagni, 101 ff.] arguing from fundamentals, that Ptolemy was himself active under Alexander, therefore cannot have been unbiased in his treatment of his own career, he goes on to illustrate, in terms of military commands, how Ptolemy on occasions exaggerated his own achievements, and on occasions disagreed with what other authors had to say about his own activities. Moreover, we can add that this exaggeration was not limited solely to military affairs. The silence about the other Macedonian nobles, which Strasburger noticed, is more insidious than at first appears: for it is used to exaggerate Ptolemy's own importance. In the 'conspiracy of the pages', which led to Callisthenes' arrest, Curtius' version1 [C(urtius) 8. 6. 22.] -- which we have no reason to doubt in outline -- has it that the conspiracy was revealed in the first instance to Ptolemy and Leonnatus, who duly brought matters to a head by informing Alexander (and who, by implication, took the credit of saving the king's life). Arrian's version is broadly similar, but the credit for bringing the conspiracy to Alexander's notice there belongs to Ptolemy alone: Leonnatus does not feature in his account, and there is no reason why Arrian should have omitted him, had Ptolemy mentioned his part.2 [A. 4. 13. 7.]

Since Ptolemy exaggerated his own activities in this way, he also, inevitably, depreciated the activities of his colleagues. In the case we have just noticed. Leonnatus' reputation would have suffered were Arrian's (Ptolemy's) version the only one to have survived. Exaggeration of Ptolemy's own activities is perhaps to be expected, and we can take precautions against it. But his insidious distortion by the simple omission of important facts about his colleagues is clearly not intended only to throw Alexander's own activities into relief, and to make them alone seem relatively more important. Ptolemy clearly used the method more widely than has hitherto been thought, and while he uses it to exaggerate discreetly his own career (often without actually lying -- a characteristic which appealed to Arrian!), we must explore whether it was also used, equally discreetly, to denigrate his later opponents. Few of his later opponents were, in fact, sufficiently important under Alexander to feature largely in Ptolemy's narrative. But there are cases which seem to offer primafacie evidence, Antigonus, Aristonous, and Perdiccas.3 [Otto (ap. H. Berve, Das Alexanderreich auf prosopographischer Grundlage (2 vols., Munich, 1926), ii, 351 n. 6), suggests that Seleucus' military career under Alexander has also been suppressed -- though he does not say who might have suppressed it. This is an unnecessary assumption and cannot be demonstrated (as Berve, loc. cit., points out), since no source supplies much information about Seleucus under Alexander, Berve's own suggestion is quite satisfactory, that Seleucus simply was not important at the time.] Since the case of Antigonus is inconclusive, I shall deal with it first.

In his examination of some information which Curtius provides, and which he thinks Arrian ought to have, Tarn deals with the case of Antigonus.4 [Alexander, ii. 110-11.] Antigonus was appointed to the satrapy of Phrygia Major in 334, which he retained until Alexander's death. After Issus, in 333, Antigonus had a major success in dealing with the remains of the Persian army which tried to escape through Asia Minor. This we know only from Curtius.5 [C. 4. I. 35.] It is not in Arrian, and the reasonable conclusion is that it was not in Ptolemy. Tarn attributed this to Ptolemy's hostility towards Antigonus: 'Ptolemy was not going to relate the acta of one who had been his most bitter enemy.'6 [Alexander, ii. 110; cf. Pearson, Lost Histories, 192 (briefly).] And since it is clear that distortion by omission was peculiarly Ptolemy's among the Alexander historians, Tarn's interpretation has a prima-facie plausibility. Yet in this instance Ptolemy can be defended: for Antigonus' activities in Phrygia after 333 were no part of the Alexander-centred story favoured both by Ptolemy and by Arrian: they were essentially off-stage activities, however important in themselves. Even if Ptolemy had recorded Antigonus' success, there is no reason for Arrian to have followed him in this. Moreover, the manner of Tarn's argument begs a large question about the date at which Ptolemy wrote: he accepts the common assumption that Ptolemy wrote late in life, therefore after he had been hostile to Antigonus (after 314).1 [Alexander, ii. 110; cf. 43.] This may be reasonable; but if Ptolemy wrote before 314, there can clearly be no question of his having been openly hostile to Antigonus at the time of his writing, and therefore no question of his having concealed Antigonus' activities through jealousy. We shall return to this point later. It is sufficient for the present to notice that there is no conclusive reason for seeing hostile bias in Antigonus' omission.

The second of our examples is more interesting. Again, Tarn has drawn attention to it.2 [Ibid. 109.] The man in question is Aristonous, about whom essential information is preserved in Curtius alone, and though Arrian mentions him twice, neither instance comes from Ptolemy. The strange thing is that Aristonous was an important man at the court; he was a somatophylax [bodyguards of high-ranking people] at least as early as 326, since Arrian cites him in a list of somatophylakes, which he took from Aristobulus, when Peucestas was made somatophylax in 325; and Aristonous is also named later as 'Alexander's somatophylax'.3 [A. 6. 28. 4; cf. Strasburger, Ptolemaios und Alexander, 46; A. succ. (=F. Jacoby, FGH no. 156), frg. 10, 6.] The only other mention in Arrian comes from Nearchus: Aristonous is named as one of the trierarchs [the title of officers who commanded a trireme, an ancient vessel and a type of galley.] on the Indus.4 [A. Ind. 18. 5.] It is Curtius who gives us details of Aristonous' sole known claim to fame under Alexander. At the capture of the city of the Malli, Aristonous is one of those who, together with Peucestas, Timaeus, and Leonnatus, fought to protect Alexander's body, and was wounded for his pains.5 [C. 9. 5. 15 ff.] Arrian, as is well known, uses the discrepancies among the accounts of this battle for a discussion of his source material, but his narrative, probably taken from Ptolemy,6 [A. 6. 9. 10; cf. Strasburger, Ptolemaios und Alexander, 45.] features Peucestas, Leonnatus, and an otherwise unknown Abreas, a dimoirites [half-file leader]. Aristonous is not mentioned. Arrian admits that accounts vary; all are agreed on Peucestas, but they do not agree on Leonnatus and Abreas.7 [A. 6. 11. 7.] It is clear that Ptolemy must have provided the account which Arrian follows, yet, as Arrian himself admits, Ptolemy was not himself present at the battle;8 [A. 6. 11. 8.] and Curtius, for one, found information about Aristonous elsewhere -- but although he knew Ptolemy's book, he chose to ignore Ptolemy's trivia about the insignificant Abreas. The conclusion which immediately presents itself is that Ptolemy has deliberately concealed Aristonous' bravery, and chosen instead to feature the unimportant Abreas; were it not for Aristobulus' list of somatophylakes, Nearchus' list of trierarchs, and Curtius' wide reading and good sense, we should know precisely nothing about Aristonous under Alexander.

This would be particularly odd in view of the fact that Aristonous was an important man after Alexander's death. Arrian's Successors, taking information from Hieronymus of Cardia, lists him among the nobles who supported Perdiccas against Meleager in the first struggle at Babylon in June 323; Curtius also makes him prominent at Babylon, and Curtius was also probably using the reliable Hieronymus.9 [A. succ. 2; C. 10. 6. 16 f. I shall show in JHS 1970 C.'s probable use of Hieronymus for his account of events at Babylon.] In this prominence at Babylon may lie the explanation of Ptolemy's silence about Aristonous under Alexander. For Aristonous was a firm supporter of Perdiccas at Babylon and after; and the speech which Curtius attributes to Aristonous at Babylon is not only the statement of one fully committed to supporting Perdiccas, but is also the first speech after Ptolemy's own intervention in the struggle, and is largely responsible for Ptolemy's proposal's being ignored. Moreover, this was not Aristonous' sole action directly against Ptolemy's interests: the Vatican papyrus fragment of Arrian's Successors shows him in action on Perdiccas' behalf in Cyprus, at the time when the leading Cypriot kings had allied with Ptolemy against Perdiccas, and when Perdiccas was in the process of invading Egypt in 320.1 [A succ. frg. 10, 6. On the date cf. E. Manni, RAL ser. 8, iv (1949), 53 ff.] Ptolemy clearly had reason for thinking Aristonous hostile, and for deliberately suppressing his activities under Alexander.2 [The remaining information about Aristonous after Perdiccas' death shows him only indirectly opposed to Ptolemy: he joined Olympias -- whether or not he was attached to Polyperchon first -- and fought for her against Cassander in 316 (Diod. 19. 35. 4), and was her governor of Amphipolis until her surrender to Cassander, when he was murdered by Cassander (Diod. 19. 51. 1 ff.). Although Ptolemy was nominally friendly towards Cassander, it is difficult to see anything in this later career of Aristonous which would exacerbate Ptolemy's hostility towards him.]

Concealment -- surely deliberate -- by Ptolemy of his enemy's earlier activities, which alone explain why Aristonous was at all prominent among the nobles at Babylon, leads us directly to an examination of Ptolemy's attitude to Perdiccas himself under Alexander, for Perdiccas proved to be Ptolemy's chief enemy -- though only comparatively briefly -- after Alexander's death: he was the only man to turn the whole might of the central government's power and propaganda against Ptolemy's possession of Egypt. There was every reason for Ptolemy to be hostile towards Perdiccas as towards his lieutenant Aristonous; and we shall see that his method of distortion by suppression was also employed in Perdiccas' case -- naturally, much more widely, inasmuch as Perdiccas was a more important man, than with Aristonous. We shall therefore proceed by comparing the picture of Perdiccas' career as it emerges from Ptolemy, on the one hand, and from the non-Ptolemaic sources on the other.

First, it is clear that a great deal of formal information, about battle alignments and commands, is common to all sources; and since this seems to be fuller and more accurate before the death of Callisthenes than after, it may have come in the first instance from Callisthenes' history, and have reached our extant authors either directly, or through Ptolemy and Aristobulus (Arrian), Clitarchus (Diodorus and ? Curtius), or others. It is therefore quite meaningless for our purpose that (for instance), both Curtius and Arrian mention the presence of Perdiccas' taxis in the dispositions before the battle of Issus, and that they are joined by Diodorus in giving the same information for Gaumela.3 [References in Berve, Das Alexanderreich, ii. 213-14.] If battles have to be described in detail, it is clearly important that the dispositions should be described. These purely formal mentions of Perdiccas' presence account for no fewer than eight out of eighteen references to him in Arrian, where he relies on Ptolemy, only four out of twenty in non-Ptolemy. Some of the remainder are insignificant for our purpose: for instance, the fact that Perdiccas was one of Philip's bodyguards is recorded only by Diodorus;4 [Diod. 16. 94. 4.] but there is no essential reason why Ptolemy (or Arrian) should have mentioned this detail. There is no point in discussing such inconclusive details: we shall therefore stick to such instances as shed some light on our investigation.

The first of these is very important, for it is a direct conflict between an attested fragment of Ptolemy and Diodorus, over Perdiccas' part in Alexander's destruction of Thebes in 335.1 [A. 1. 8. 1 ff. = FGH no. 138, frg. 3; Diod. 17. 12. 3 ff.] Ptolemy's tendency throughout his book is to apologize for Alexander, wherever he can prevent his distortion from being too obvious, and to depict him as being correct and right and his actions justified. Ptolemy's version of the destruction of Thebes -- a difficult enough problem for his Tendenz so early in his book -- is that the crucial attack which ultimately captured the city was started by Perdiccas without Alexander's orders, and that Alexander had to go to his rescue, and by so doing captured the city. The version has the clear merit for Ptolemy of partially absolving Alexander of the blame for Thebes' destruction; and this purpose becomes even clearer as his account progresses, when the Phocians, Plataeans, and other Boeotians are said to have been more prominent than the Macedonians in sacking the city.2 [A. 1. 8. 8.] Here, Ptolemy chooses the ill discipline of Perdiccas as his chief means of absolving Alexander from the distasteful responsibility for destroying Thebes. His dual purpose is clear enough, and has often been recognized, particularly when it is confronted with Diodorus' version which (much more soberly and reasonably) has Perdiccas acting on Alexander's orders, and the other Greeks joining in the destruction only when it is already under way.3 [Diod. 17. 12. 3.] Tarn preferred Ptolemy; but, long before, Berve had rightly thought Diodorus' version more trustworthy.4 [Tarn, Alexander, i. 7-8; Berve, Das Alexanderreich, ii. 313.]

This is one of the few preserved traceable examples where Ptolemy distorted other than by omission.5 [For some other important examples (not involving Perdiccas) cf. Badian, Studies, 258; Welles, Miscellanea Rostagni, 101 ff.] But omission can hurt Perdiccas just as well. At the siege of Tyre we have to look to Curtius to find the fact that Alexander at one stage left Perdiccas and Craterus in joint command of the siege operations while he went against some Arabs.6 [C. 4. 3. 1; cf. A. 2. 20. 4.] This could conceivably be an omission of Arrian's, so undue weight should not be placed upon it. But when we come to Gaugamela Ptolemy is clearly culpable: a list of nobles wounded in the battle is uniformly given by Diodorus and Curtius as Hephaestion, Perdiccas, Coenus, and Menidas; Arrian has merely Hephaestion, Coenus, and Menidas, omitting Perdiccas.7 [Diod. 17. 61. 3; C. 4. 16. 32; cf. A. iii. 15. 2.] Arrian himself had no reason to deprive Perdiccas of his glory: his omission must be Ptolemy's responsibility. Furthermore, we owe to a random mention in Curtius our knowledge that Perdiccas had already reached the high rank of somatophylax by 330, for he participated in the Philotas affair in this capacity. Ptolemy himself, we know, did not become somatophylax until after the affair, as a direct result of a vacancy created by the purge which followed.8 [C. 4. 8. 17 (Perdiccas); A. 3. 27. 5 (Ptolemy).]

From this time onwards Ptolemy himself had the same high status as Perdiccas, and they were often associated. But it can scarcely be an accident that Ptolemy's own activities are given much more prominence in Arrian than Perdiccas' -- or indeed, than any of the other nobles': we have already seen how Leonnatus' part in discovering the conspiracy of the pages was suppressed by Ptolemy -- in their personal association with Alexander. In Sogdiana in 329 Curtius alone9 [C. 7. 6. 19-21.] mentions that Perdiccas and Meleager were left in charge of a siege; and in the next spring, when Alexander split up the army into five sections, commanded respectively by himself, Hephaestion, Perdiccas, Ptolemy, and Coenus and Artabazus jointly, Ptolemy is the only man explicitly called somatophylax, yet Hephaestion and Perdiccas were also members of the corps.1 [A. 4. 16. 2; cf. Berve, Das Alexanderreich, i. 25 ff.] This might be quite accidental. But it is odd that Arrian here uses this distinguishing phrase in addition to his usual defining phrase, 'Ptolemy, son of Lagus'. There is no obvious need to mention that Ptolemy was somatophylax. It seems to carry the false implication, which may well be deliberate, that all the others were not.

Another conflict of evidence occurs in connection with the death of Clitus in Maracanda, in winter 328/7. Alexander held a party in connection with a sacrifice to the Dioscuri, in the course of which Alexander's achievements were openly praised in terms which offended some of the older Macedonians, since they implied depreciation of the achievements of Phllip. Clitus objected, and Alexander tried to kill him, but was at first restrained. There are different versions of the incident from here on, but all sources agree that the upshot was that very soon after the first provocation the party provided another opportunity for Alexander, and this time Clitus was duly murdered.

Arrian's main version of the first part of the incident, in which Alexander was at first restrained, is vague. He says simply that Alexander was restrained by 'some of his drinking companions'.2 [A. 4. 8. 7.] He also cites explicitly Aristobulus, whose version was that Ptolemy rushed Clitus away before any damage could be done, but that Clitus rushed back and presented Alexander with his opportunity.3 [A. 4. 8. 9.] Aristobulus' version is clearly an attempt to exonerate Alexander, and to depict his action as duly provoked -- which is consonant with his reputation in later antiquity as a flatterer of Alexander.4 [Cf. Pearson, Lost Histories, 150 ff., with Badian's comments, Studies, 255-6.] If Arrian is here following his usual custom, his main version will be Ptolemy's, while he cites Aristobulus' version as a variation. In this case Ptolemy chose to conceal his own part in the affair under the blanket term which Arrian gives as [x]. In outline, Curtius' account agrees with Arrian's first version, but gives more detail: [x] becomes Ptolemy and Perdiccas, aided by Lysimachus and Leonnatus.5 [C. 8. 1. 43. ff.] Where Curtius' source found these names is not clear: Plutarch's account of the events, which perhaps comes from Chares, does not mention them.6 [Plut. Alex. 50-1; cf. Pearson, Lost Histories, 60.] It is difficult to believe that they are invented -- though it is not impossible. However, if they are (more or less) correct, Ptolemy's vague phrase can be seen to have concealed his own participation; but it has also concealed the participation of others. It is easy enough to see that Ptolemy himself was not proud of his involvement in the highly discreditable episode, and if he omitted his own part, he could scarcely allow others to be prominent.

However, the consensus of modern opinion is that Arrian's main version is not here drawn from Ptolemy.7 [So Strasburger, Ptolemaios und Alexander, following Schwartz, R.E. s.v. 'Arrianos', 1240, and Jacoby, FGH 11 D, 517.] If this is correct -- and there are good grounds for it -- it must imply that Ptolemy simply omitted the whole unsavoury episode, a practice entirely in accordance with his normal technique of suppressing the inconvenient or unpalatable. In so doing, of course, he has also omitted -- as we have already seen from discussing the implications of [x] -- both his own part and that of his colleagues. However we regard the question of Arrian's source, we clearly have here a further example of the discreet silence which has already been seen to be the chief characteristic of Ptolemy's propaganda technique. Unfortunately for Ptolemy, his was not the only version of the incident to survive; Aristobulus chose him as the deux ex machina for his own justification of Alexander's conduct. Someone much more straightforward provided information which perhaps Clitarchus wrote up for Curtius' use. For despite some (trivial) dramatic additions for which Curtius himself might easily be responsible, Curtius' version shows fewer signs of tendentious distortion than either of Arrian's, and is therefore likely (in outline) to be closer to the truth. Also the fact that it is not altogether incompatible with Plutarch's version -- which, if from Chares, will represent an eyewitness account -- suggests the same conclusion.

From the death of Clitus to the end of the Indian campaign relatively little evidence for our purpose is available: both Curtius and Arrian confirm that Perdiccas was sent ahead of the main expedition with Hephaestion to arrange the bridging of the Indus; and though Arrian gives much more prominence to Ptolemy's activities than does Curtius, this is explicable from Arrian's use of Ptolemy, who, it is clear, also liked where possible to give his own activities a discreet prominence.1 [C. 8. 10. 2 ff.; A. 4. 22. 7 ff.] Nor can much be made of the remaining instances of Perdiccas' activities as mentioned by Arrian; they are mostly either simple military commands with little or no detail given, or references to groups of men among whom Ptolemy also is mentioned.2 [Military: A. 6. 6. 4 ff.; 6. 16. 1.; cf. C. 9. 1. 19. Groups: A. 5. 13. 1; 7. 4. 5; cf. C. 8. 14. 15.] Only one more direct reference may reflect Ptolemy's bias in action; the occasion is the attack on the city of the Malli, where Alexander was almost fatally wounded.3 [A. 6. 9. 1 ff., cf. Schwartz, R.E. s.v. 'Arrianos', 1241; Strasburger, Ptolemaios und Alexander, 45.] The incident as presented by Arrian, who is no doubt influenced by Ptolemy's presentation, does nothing to enhance Perdiccas' military reputation; for it was directly because of the slowness in action of his section of the army that Alexander was cut off and wounded. If this does reflect Ptolemy, it is consistent with his general attitude to Perdiccas.

Crucial omissions now remain to be considered, for they constitute the body of facts which alone explain how Perdiccas was, at the time of A1exander's death, quite pre-eminent among the Macedonians; if we only had Arrian, with his emphasis, taken from Ptolemy, on Alexander's own achievements, it would come as a totally unexplained phenomenon to find (even in Arrian's own book on the successors) Perdiccas' immediate dominance at Babylon after Alexander's death. Ptolemy's subtle distortion by suppression must clearly be at work again, with its purpose of emphasizing Alexander's supremacy over all. The vital facts which Ptolemy has suppressed are that Perdiccas, on Hephaestion's death in 324, virtually succeeded to Hephaestion's position as chief companion of the king and second-in-command of the empire. Diodorus, following Clitarchus -- who is likely to have been well informed on these events, since he may have been an eyewitness; but in any case he had no axe to grind and no reason to falsify details which would be widely known -- says that Perdiccas was given the highly personal and honorific task of conveying Hephaestion's body to Babylon;4 [Diod. 17. 110. 8. On the date of Clitarchus see (most recently) Badian, PACA viii ( 1965), 5 ff.] and Diodorus is supported by Plutarch -- here both using Hieronymus of Cardia, whose close association with Eumenes made him well informed on court matters -- in saying that Perdiccas succeeded to Hephaestion's position as chiliarch of the companion cavalry -- a military command which by now implied that its holder would be Grand Vizier head of government of many sovereign states in the Islamic world.].1 [Diod. 18. 3. 4; Plut. Eumenes, I. Tarn, JHS, 1921, 4 ff., argues unconvincingly that these are based on Duris -- yet even Duris cannot always have been wrong! On Hieronymus see T.S. Brown, AHR lii (1946-7), 684 ff.] Ptolemy found this an opportunity for discreet concealment. Arrian records Ptolemy's information that Alexander never appointed another commander for Hephaestion's chiliarchy, but that it remained known as 'Hephaestion's chiliarchy', and kept the same standard. This seems to contradict Diodorus and Plutarch, yet it is not incompatible. That we cannot simply choose to believe Ptolemy's version against that of the others is clear from the additional fact that in the same passage Plutarch preserves a promotion consequent on that of Perdiccas, Eumenes' appointment to command Perdiccas' taxis. Perdiccas must have been given the temporary command of Hephaestion's chiliarchy -- for reasons we need not investigate here -- which accordingly retained its name and standard. Presumably Perdiccas' taxis, now commanded by Eumenes, similarly retained its former name and standard. Arrian omits these crucial promotions; indeed, he implies that they did not take place. The dissimulation is clear; it must be Ptolemy's, and Perdiccas' reputation is again the chief sufferer.2 [A. 7. 14. 10. This explanation of the contradiction in the sources seems more satisfactory than that of Berve, Das Alexanderreich, ii. 315-16, and Tarn (tentatively, in Alexander, i. 117) that Perdiccas did the duties of the office without the name; it is far from clear that the Macedonian monarchy employed such over-subtle distinctions. Possible hostility to Eumenes, also apparent in this omission, will be from Eumenes' later close association with Perdiccas. Unfortunately we cannot trace this in any detail in Ptolemy's book.]

Lastly Curtius, probably taking his information from Clitarchus -- who had no reason to invent it -- must be reliable when he makes Perdiccas Alexander's confidant on his death-bed;3 [C. 10. 5. 8.] and Curtius, Diodorus, and Justin, all probably using Hieronymus who, through Eumenes, would know the fact from its importance in the subsequent struggle at Babylon, record Alexander's giving Perdiccas his signet ring. Tarn denied that this was fact because Ptolemy did not say it.4 [Diod. 17. 117. 3; 18. 2. 4; C. 10. 5. 4; Justin, 12. 15. 12. Tarn, JHS 1921, 4 ff.; cf. also M. J. Fontana, 'Le lotte per la successione di Alessandro Magno', 259 ff. (in Atti della accademia di scienze, lettere e arti di Palermo, xviii, II, 1957-8). Good discussion in Badian, HSPh lxxii (1967), 185 n. 12.] But his argument from silence is not at all cogent. Ptolemy, as we have seen, had every reason for suppressing Perdiccas' prominence and there is no justification any longer for regarding him as the sole straight-forward purveyor of all truth.

Ptolemy's suppression of important details about Aristonous and Perdiccas seems proved, in so far as anything of this kind can ever be proved. The reason for the suppression must originate in their co-operation against Ptolemy's separatist inclinations in Egypt after Alexander's death. We can perhaps go further and see Ptolemy's discreetly apologetic portrait of Alexander himself, and his generally uninformative treatment of his officers, as also originating in these years. For by depicting Alexander as supreme, by implication Ptolemy depicted Alexander's officers as all being on the same level of prominence. To depict the officers as equals under Alexander, to suppress the outstanding prominence of Perdiccas in the last years, was tantamount to depicting his own position after 323 as being based on an equivalent prestige to Perdiccas'. This was likely to be a much more effective means of propaganda than if Ptolemy had obviously exaggerated his own status under Alexander, for that would be expected; and the fact that we have to search for this type of personal exaggeration is evidence that Ptolemy avoided making himself invidiously prominent in his book.

This bias which we have illustrated against Perdiccas and Aristonous -- leaving aside the doubtful case of Antigonus -- might have some bearing on the date at which Ptolemy wrote his history. Badian has already suggested that the traditional period for the composition -- Ptolemy's extreme old age in the 280s B.C. -- should be reconsidered: his re-examination of the meagre evidence for the relative dates of Ptolemy and Aristobulus shows it to be entirely inconclusive;1 [Badian, Studies, 256 ff. For the traditional view, cf. Pearson, Lost Histories, 193 ff.] and the traditional purpose for Ptolemy's book, to set the record straight, is equally unconvincing. In addition to the important instances which Badian cites of Ptolemy's suppression of crucial details of court history, which in themselves constitute a severe indictment against Ptolemy's good faith, the more personal animosity which we have demonstrated offers further evidence of a distinct purpose behind Ptolemy's Tendenz. Badian suggests that his book might have been written during the early part of his career in Egypt, at the time when, having snatched Alexander's body from Perdiccas' control and buried it in Egypt, he seems to have been making some claim to be regarded as Alexander's successor.2 [Studies, 258.]

Certainly, the traditional late date offers no convincing reason for Ptolemy's purpose: there could be no urgency giving edge to his hostility towards Perdiccas and Aristonous, no urgency to his suppression of unsavory details about Alexander, if he wrote when his own acknowledged kingship had existed for nearly twenty years,3 [From 305/4; cf. A. E. Samuel, Ptolemaic Chronology (Munich, 1962), 4 ff.] his actual control of Egypt for nearly forty. What point was there, at this late stage of his life, in justifying himself in this over-subtle way? If we take an earlier date, however (let us say sometime after 320, when Perdiccas was assassinated in Egypt while attacking Ptolemy, and Ptolemy had access to such documentary material as was collected at the royal headquarters), Ptolemy had more reason for producing the kind of book he did. The previous year he had gained the prestige of possessing Alexander's corpse; he was investing massive resources in developing the city of Alexander, Alexandria, as his capital; in every way his satrapy was to be dominated by the prestige (and the physical remains) of Alexander. It is surely in this general context that his Alexander-centred history assumes its greatest relevance. From this time onwards the course of events might actually be affected by what people -- particularly the Macedonians and Greeks whom he wished to encourage to support him in Egypt -- thought about Alexander. After Perdiccas' death it really mattered to Ptolemy what these people thought about Perdiccas and what kind of information they had about him. And -- perhaps most importantly -- what Alexander had thought about Perdiccas, for this was an immediate issue. After Perdiccas' death and in the context of an Alexander-conscious Egypt which was on the defensive, the general levelling of the officers' prestige under Alexander and the concealment of Perdiccas' closeness to Alexander in the last months of the king's life were not only important: they might even have been the crucial factors in retaining the long-term loyalty or Ptolemy's Macedonian supporters. On Alexander Ptolemy built his kingdom. His publicized view of Alexander and of the careers of his colleagues (and of himself) under Alexander is vitally conditioned by this fact.

[admin]

Reckonings dated from a historical event
by Britannica
Accessed: 6/26/21

The inscriptions of the Buddhist king Aśoka (c. 265–238 BC) give the first epigraphical evidence of the mode of reckoning from a king’s consecration (abhiṣeka). In these inscriptions (Middle Indian language in India or Greek and Aramaean in what is now Qandahār, Afghanistan) the dates are indicated by the number of complete years elapsed since the king’s consecration. But the earlier existence of a reckoning of duration of reigns and dynasties is evidenced by the testimony of the Greek historian Megasthenes, who in 302 BC was the ambassador of Seleucus I Nicator, founder of the Seleucid Empire, to the court of Chandragupta Maurya, Aśoka’s grandfather. According to Megasthenes, the people of the Magadha kingdom, with its capital Pāṭaliputra (Patna), kept very long dynastic lists, preserved in the later Sanskrit Purāṇas (legends of the gods and heroes) and later Buddhist and Jain chronicles. They generally indicate, in years or parts of years, the duration of each reign.

Similar records of other periods and regions exist, and a relative chronology may be established. Unfortunately, it is not always possible to connect them with any absolute chronology, the precise dates of the reigns given being still unsettled. For example, in the Scythian period of the history of northern India, several inscriptions are dated from the beginning of the reign of Kaniṣka, the greatest king of the Asian (Kushān) invaders, but his dates are still uncertain (AD 78, 128–129, 144, etc., have been suggested for the beginning of a Kaniṣka era).

Other records give regnal years that can be linked with absolute chronology through other data—e.g., those of several rulers of the Rāṣṭrakūṭa of the Deccan.

The dynastic eras, founded by several rulers and kept up or adopted by others, are also numerous. The most important were the Licchavi era (AD 110), used in ancient Nepal; the Kalacuri era (AD 248), founded by the Abhūrī king Īśvarasena and first used in Gujarāt and Mahārāshtra and later (until the 13th century) in Madhya Pradesh and as far north as Uttar Pradesh; the Valabhī era (AD 318, employed in Saurāṣṭra) and the Gupta era (AD 320), used throughout the Gupta Empire and preserved in Nepal until the 13th century. Later came the era of the Thakuri dynasty of Nepal (AD 395), founded by Aṃśuvarman; the Harṣa era (AD 606), founded by Harṣa (Harṣavardhana), long preserved also in Nepal; the western Cālukya era (AD 1075), founded by Vikramāditya VI and fallen into disuse after 1162; the Lakṣmaṇa era (AD 1119), wrongly said to have been founded by the king Lakṣmaṇasena of Bengal and still used throughout Bengal in the 16th century and preserved until modern times in Mithilā; the Rājyabhīṣekasaka or Marāthā era (1674), founded by Śivājī but ephemeral.

Later, instead of the beginning of a reign or of a dynasty, the death of a religious founder was adopted as the starting point of an era. Among Buddhists the death of the Buddha and among the Jains the death of the Jina were taken as the beginning of eras. The Jain era (vīrasaṃvat) began in 528 BC. Several Buddhist sects (no longer existing in India) adopted different dates for the death (Nirvāṇa) of the Buddha. The Buddhist era prevailing in Ceylon and Buddhist Southeast Asia begins in 544 BC.

Historical events, now obscure, were the basis of the two most popular Indian eras: the Vikrama and the Śaka.

The Vikrama era (58 BC) is said in the Jain book Kālakācāryakathā to have been founded after a victory of King Vikramāditya over the Śaka. But some scholars credit the Scytho-Parthian ruler Azes with the foundation of this era. It is sometimes called the Mālava era because Vikramāditya ruled over the Mālava country, but it was not confined to this region, being widespread throughout India. The years reckoned in this era are generally indicated with the word vikramasaṃvat, or simply saṃvat. They are elapsed years. In the north the custom is to begin each year with Caitra (March–April) and each month with the full moon. But in the south and in Gujarāt the years begin with Kārttika (October–November) and the months with the new moon; in part of Gujarāt, the new moon of Āṣāḍha (June–July) is taken as the beginning of the year. To reduce Vikrama dates to dates AD, 57 must be subtracted from the former for dates before January 1 and 56 for dates after.

The Śaka, or Salivāhana, era (AD 78), now used throughout India, is the most important of all. It has been used not only in many Indian inscriptions but also in ancient Sanskrit inscriptions in Indochina and Indonesia. The reformed calendar promulgated by the Indian government from 1957 is reckoned by this era. It is variously alleged to have been founded by King Kaniṣka or by the Hindu king Salivāhana or by the satrap Nahapāna. According to different practices, the reckoning used to refer to elapsed years in the north or current years in the south and was either solar or luni-solar. The luni-solar months begin with full moon in the north and with new moon in the south. To reduce Śaka dates (elapsed years) to dates AD, 78 must be added for a date within the period ending with the day equivalent to December 31 and 79 for a later date. For Śaka current years the numbers to be added are 77 and 78. The official Śaka year is the elapsed year, starting from the day following that of the vernal equinox. A normal year consists of 365 days, while the leap year has 366. The first month is Chaitra, with 30 days in a normal year and 31 in a leap year; the five following months have 31 days, the others 30.

A Nepalese era (AD 878) of obscure origin was commonly used in Nepal until modern times. The years were elapsed, starting from Kārttika, with months beginning at new moon. Another era, the use of which is limited to the Malabār Coast (Malayalam-speaking area) and to the Tirunelveli district of the Tamil-speaking area, is connected with the legend of the hero Paraśurāma, an avatar (incarnation) of the god Vishnu. It is called the Kollam era (AD 825). Its years are current and solar; they start when the Sun enters into the zodiacal sign of Virgo in north Malabār and when it enters into Leo in south Malabār. It is sometimes divided into cycles of 1,000 years reckoned from 1176 BC. Thus, AD 825 would have been the first year of the era’s third millennium.

Eras based on astronomical speculation

During the period of elaboration of the classical Hindu astronomy, which was definitively expounded in the treatises called siddhāntas and by authors such as Aryabhata (born AD 476), Varāhamihira, Brahmagupta (7th century AD), etc., the ancient Vedic notions on the cycle of years, embracing round numbers of solar and lunar years together, were developed. On the one hand, greater cycles were calculated in order to include the revolutions of planets, and the theory was elaborated of a general conjunction of heavenly bodies at 0° longitude after the completion of each cycle. On the other hand, cosmologists speculated as to the existence of several successive cycles constituting successive periods of evolution and involution of the universe. The period calculated as the basis of the chronology of the universe was the mahāyuga, consisting of 4,320,000 sidereal years. It was divided into four yugas, or stages, on the hypothesis of an original “order” (dharma) established in the first stage, the Kṛta Yuga, gradually decaying in the three others, the Tretā, Dvāpara, and Kali yugas. The respective durations of these four yugas were 1,728,000, 1,296,000, 864,000, and 432,000 years. According to the astronomer Aryabhata, however, the duration of each of the four yugas was the same—i.e., 1,080,000 years. The basic figures in these calculations were derived from the Brahmanical reckoning of a year of 10,800 muhūrta (see calendar: The Hindu calendar), together with combinations of other basic numbers, such as four phases, 27 nakṣatras, etc. The movement of the equinoxes was at the same time interpreted not as a circular precession but as a libration (periodic oscillation) at the rate of 54 seconds of arc per year. It is in accordance with these principles that the calculation of the beginning of the Kali Yuga was done in order to fix for this chronology a point starting at the beginning of the agreed world cycle. Such a beginning could not be observed, since it was purely theoretical, consisting of a general conjunction of planets at longitude 0°, the last point of the nakṣatra Revati (Pisces). It has been calculated as corresponding to February 18, 3102 BC (old style), 0 hour, and taken as the beginning of the Kali era. In this era, the years are mostly reckoned as elapsed and solar or luni-solar.

In Hindu tradition the beginning of the Kali era was connected with (1) events of the Mahābhārata war; (2) King Yudhiṣṭhira’s accession to the throne; (3) 36 years later, King Parikṣit’s consecration; and (4) the death of Lord Krishna. Years of the era are still regularly given in Hindu almanacs.

An era resting upon a fictitious assumption of a complete 100-year revolution of the Ursa Major, the Great Bear (saptarṣi), around the northern pole was the Saptarṣi, or Laukika, era (3076 BC), formerly used in Kashmir and the Punjab. The alleged movement of this constellation has been used in Purāṇa compilations and even by astronomers for indicating the centuries.

Two chronological cycles were worked out on a basis of the planet Jupiter’s revolutions, one corresponding to a single year of Jupiter consisting of 12 solar years and the other to five of Jupiter’s years. The second, the bṛhaspaticakra, starts, according to different traditions, from AD 427 or from 3116 BC. Before AD 907 one year was periodically omitted in order to keep the cycle in concordance with the solar years. Since 907 the special names by which every year of the cycle is designated are simply given to present years of the almanac.

Side-by-side with Hindu and foreign eras adopted in India, several eras were created in the country under foreign influence, chiefly of the Mughal emperor Akbar: Bengali San (AD 593), Amli of Orissa and Vilayati (AD 592), Faṣlī (AD 590, 592, or 593 according to the district), and Sursan of Mahārāshtra (599).

Egyptian

At the end of the 4th millennium BC, when King Menes, the first king of a united Egypt, started his reign, the ancient Egyptians began to name each year by its main events, presumably to facilitate the dating of documents. These names were entered into an official register together with the height of the Nile during its annual inundation. Short notes at first, the year names developed into lengthy records of historical and religious events, especially of royal grants to the gods. These lists grew into annals, which were kept during the entire history of Egypt so that later kings could, after important events, consult the annals and ascertain whether a comparable occurrence had happened before. Unfortunately, these annals are lost. Only fragments from the 1st to the 5th dynasty (c. 3100–c. 2345 BC) are preserved, copied on stone. These fragments, however, are in such poor condition that they raise more chronological problems than they solve.

The Egyptian priests of the Ramesside period (c. 1300 BC) copied the names and reigns of the kings from Menes down to their time from the annals, omitting all references to events. Even this king list would have given a safe foundation of an Egyptian chronology, but the only extant copy, on a papyrus now kept at the Museo Egizio in Turin, has survived only in shreds, entire sections having been lost. Extracts from this king list, which name only the more important kings, are preserved in the temples of the kings Seti I and Ramses II at Abydos and on the wall of a private tomb at Ṣaqqārah (now in the Egyptian Museum), but they give little help in chronological matters.

When the Greeks began to rule Egypt after the conquest of Alexander the Great, King Ptolemy II Philadelphus, hoping to acquaint the new ruling class with the history of the conquered country, commissioned Manetho, an Egyptian priest from Sebennytus, to write a history of Egypt in the Greek language. As Manetho had access to the ancient annals, he added some of their entries to his list of kings and reigns, especially during the first dynasties. The more he progressed in time, the more he added semihistorical traditions and stories as they were composed by the Egyptian priests to discuss moral problems in the disguise of a historical “novel.” There had been, undoubtedly, fewer historical facts in Manetho’s history than one might expect. But Manetho’s work, too, is lost except for some excerpts used by Sextus Julius Africanus and Eusebius in writing their chronicles. These, in turn, represented the material used in part by George Syncellus in the 8th century AD. During copying and recopying, Manetho’s text clearly suffered many changes, unintentionally or on purpose. The figures of the reigns, especially of the older dynasties, for instance, were enlarged when some of the early Christian historians tried to equate King Menes with Adam. In addition, the excerpts were done carelessly. Therefore, Manetho’s work, as handed down to us, is short of useless. Nevertheless, together with the fragments of the annals and of the king list of Turin, they create a framework of Egyptian chronology; so the division into dynasties was taken over from Manetho. But to achieve a continuous history of Egypt and to bridge the gaps left by the fragmentary state of the extant chronological material, scholars must turn to other means, particularly astronomical references found in dated texts. These are related principally to the rising of Sothis and to the new moon.

Theoretically, the Egyptian civil year began when the Dog Star, Sirius (Egyptian Sothis), could first be seen on the eastern horizon just before the rising of the Sun (i.e., 19/20 of July). As the civil calendar of the ancient Egyptians consisted of 12 months (each of 30 days) and five odd days (called epagomenal days), the civil year was a quarter of a day too short in relation to the rising of Sothis, so that the new year advanced by one day every four years. New Year’s Day and the rising of Sothis coincided again only after approximately 1,460 years, the so-called Sothic cycle. Dated documents mentioning the rising of Sothis can be translated into the present calendar by multiplying the number of days elapsed since the first day of the year by four and subtracting this sum from the date of the beginning of the particular Sothic cycle. The dates for the start of each Sothic cycle are fortunately known because the Roman historian Censorinus fixed the coincidence of New Year’s Day and heliacal rising of Sothis in AD 139. Taking into account a slight difference between a Sothic year and a year of the fixed stars, the years 1322, 2782, and 4242 BC are taken as starting points of a Sothic cycle.

There are six ancient Egyptian documents extant giving Sothis dates, but only three of these are of value. The oldest is a letter from the town of Kahun warning a priest that the heliacal rising of Sothis will take place on the 16th day of the 8th month of year 7 of a king who, according to internal evidence, is Sesostris III of the 12th dynasty. This date corresponds to 1866 BC, according to the corrected Sothic cycle. The next date is given by a medical papyrus written at the beginning of the 18th dynasty, to which a calendar is added, possibly to ensure a correct conversion of dates used in the receipts to the actual timetable. Here it is said that the 9th day of the 11th month of year 9 of King Amenhotep I was the day of the heliacal rising of Sothis—i.e., 1538 BC. This date, however, is only accurate provided that the astronomical observations were taken at the old residence of Memphis; if observed at Thebes in Upper Egypt, the residence of the 18th dynasty, the date must be lowered by 20 years—i.e., 1518 BC. The third Sothis date shows that Sirius rose heliacally sometime during the reign of Thutmose III, which lasted for 54 years, on the 28th day of the 11th month; so year 1458 BC (point of observation at Memphis) or 1438 BC (point of observation at Thebes) must have belonged to the reign of this king. From these dates it is possible to calculate the absolute dates for the reigns of the 12th dynasty, as the durations of most of the reigns of the kings belonging to this dynasty are preserved on the king list of the Turin Papyrus. On the other hand, chronologists are able to compute the reigns of the kings of the 18th dynasty by utilizing the highest dates of their documents and the figures preserved by Manetho. Historians are also helped by the fact that the Egyptians sometimes identified a certain day as “exactly new moon”; they reckoned new moon from the morning after the last crescent of the waning moon had become invisible in the east just before sunrise. As there is a 25-year lunar cycle, such ancient Egyptian moon dates could be calculated with a fair amount of certainty but of course only if the ancient Egyptians themselves observed this celestial phenomenon accurately. There is some doubt, however, as it is shown by the attempts of very competent scholars to convert these moon dates. Sometimes even moon dates given by the same papyrus contradict themselves; in another case, the date given by a document had to be amended to achieve a reasonable result. These and other examples show that ancient Egyptian statements on celestial phenomena, especially on new moons, tend to be inaccurate because of faulty or inexact observations. Therefore, every date given for a fixed reign should be used with caution as the astronomical observation on which it is based may be inexact. Sometimes they are controlled by synchronism with Babylonian, Assyrian, or Hittite king lists or, later on, by the close interconnections between Greek and Egyptian history. Sometimes even biographical data are helpful. The statements found on small stelae inside the burial ground of the holy bulls of Memphis (Apis) register the dates of birth, enthronement, and death of these animals accurately. But the more time recedes, the more the chronology of the Egyptian history becomes uncertain, even when astronomical data are available. Up till now even carbon-14 data are of no great help, as uncertainties are mostly not greater than the standard deviations to be expected in a carbon-14 calculation.

Nevertheless, Egyptologists believe themselves to be on fairly firm ground when dating the beginning of the Ancient Kingdom (1st and 2nd dynasty) about 3090 BC, the beginning of the 11th dynasty at 2133 BC, and of the Middle Kingdom (12th dynasty) at 1991 BC. The New Kingdom started at 1567 or 1552 BC, depending on a choice for the first year of Ramses II of either 1290 BC or 1304 BC—one lunar cycle earlier. The following centuries still pose many chronological questions down to 664 BC, when Greek historiography took over.

Babylonian and Assyrian

Mesopotamian chronology, 747 to 539 BC

The source from which the exploration of Mesopotamian chronology started is a text called Ptolemy’s Canon. This king list covers a period of about 1,000 years, beginning with the kings of Babylon after the accession of Nabonassar in 747 BC. The text itself belongs to the period of the Roman Empire and was written by a Greek astronomer resident in Egypt. Proof of the fundamental correctness of Ptolemy’s Canon has come from the ancient cuneiform tablets excavated in Mesopotamia, including some that refer to astronomical events, chiefly eclipses of the Moon. Thus, by the time excavations began, a fairly detailed picture of Babylonian chronology was already available for the period after 747 BC. Ptolemy’s Canon covers the Persian and Seleucid periods of Mesopotamian history, but this section will deal only with the period up to the Persian conquest (539 BC).

The chief problem in the early years of Assyriology was to reconstruct a sequence for Assyria for the period after 747 BC. This was done chiefly by means of limmu, or eponym, lists, several of which were found by early excavators. These texts are lists of officials who held the office of limmu for one year only and whom historians also call by the Greek name of eponym. Annals of the Assyrian kings were being found at the same time as eponym lists, and a number of these annals, or the campaigns mentioned in them, were dated by eponyms who figured in the eponym lists. Moreover, some of the Assyrian kings in the annals were also kings of Babylonia and as such were included in Ptolemy’s Canon.

Good progress was therefore being made when, soon after 1880, two chronological texts of outstanding importance were discovered. One of these, now known as King List A, is damaged in parts, but the end of it, which is well preserved, coincides with the first part of Ptolemy’s Canon down to 626 BC. The other text, The Babylonian Chronicle, also coincides with the beginning of the canon, though it breaks off earlier than King List A. With the publication of these texts, the first phase in the reconstruction of Mesopotamian chronology was over. For the period after 747 BC, there remained only one serious lacuna—i.e., the lack of the eponym sequence for the last 40 years or so of Assyrian history. This had not been established by the early 1970s.

Assyrian chronology before 747 BC

German excavations at Ashur, ancient capital of Assyria, yielded further eponym lists. By World War I the full sequence of eponyms was known from about 900 to 650 BC. A further fragmentary list carried the record back to about 1100 BC, and on this basis Assyrian chronology was reconstructed, with little error, back to the first full regnal year of Tiglath-pileser I in 1115 BC. Without another eponym list, a king list was needed for substantial further progress. King lists found at Ashur proved disappointing. Those fairly well preserved did not include figures for the reigns, and those with figures were very badly damaged.

In 1933, however, an expedition from the University of Chicago discovered at Khorsabad, site of ancient Dur Sharrukin, an Assyrian king list going back to about 1700 BC. But for the period before 1700 BC the list is damaged and otherwise deficient, and Assyrian chronology prior to this date is still far from clear.

Before 747 BC it was the custom of the Assyrian kings to hold eponym office in their first or second regnal year. Thus, in an eponym list, the number of names between the names of two successive kings usually equals the number of years in the reign of the first of the two kings. It would have been easy to compile a king list from an eponym list, and there is evidence that this Assyrian king list was compiled from an eponym list probably in the middle of the 11th century BC. As an eponym list is a reliable chronological source, since omission of a name entails an error of only one year, the king list, if based on one, will have preserved much of the structure of older eponym lists now lost. (Except for one fragment, no known eponym list goes back further than the beginning of the 11th century BC.)

Babylonian chronology before 747 BC

In the long interval between the fall of the last Sumerian dynasty c. 2000 BC and 747 BC there are two substantial gaps in chronology, each about two centuries long. The earlier gap is in the 2nd millennium, from approximately 1600–1400 BC, the later gap in the 1st millennium, from c. 943–747 BC. During these gaps the names of most of the kings are known, as well as the order, but usually not the length of their reigns.

A means of checking the reliability of the Babylonian king list is provided by the chronicles, annals, and other historical texts that show that a given Assyrian king was contemporaneous with a given Babylonian king. There are no fewer than 15 such synchronisms between 1350 and 1050 BC, and, when the Babylonian and Assyrian king lists are compared, they all fit in easily. Only one of them, however, provides a close approximate date in Babylonian chronology. This synchronism shows that the two-year reign of the Assyrian king Ashared-apil-Ekur (c. 1076–c. 1075 BC) is entirely comprised within the 13-year reign of the Babylonian king Marduk-shapik-zeri. The Assyrian’s dates are probably correct to within one year. Thus, if Marduk-shapik-zeri is dated so that equal proportions of his reign fall before and after that of Ashared-apil-Ekur, a date is obtained for the former that should not be in error more than six years. This synchronism constitutes a key to the structure of Babylonian chronology by providing the base date for all the reigns in the interval c. 1400–943 BC for which the Babylonian king list gives figures. All the dates thus obtained are subject to the six-year margin of error.

These synchronisms between Assyrian and Babylonian kings continue throughout the period that corresponds to the second gap in the Babylonian king list—from c. 943–747 BC. Since the Assyrian chronology in that period is firmly established, these synchronisms provide a useful framework for the structure of Babylonian chronology in that period.

The gap in the 2nd millennium BC, however, is not as easy to fill. The fact that the magnitude of the gap is uncertain constitutes the main problem in the chronology of the 2nd millennium BC and also affects the chronology of the preceding Sumerian period. The problem is not yet solved. Observations of the planet Venus made during the reign of King Ammisaduqa, less than 50 years before the end of the 1st dynasty of Babylon, permit only certain possible dates for his reign. Translated into dates for the end of the dynasty, the three most likely possibilities are 1651, 1595, and 1587 BC. The evidence is not yet conclusive and leaves uncertain what choice should be made among the three. The chronology adopted here is based on the second of these dates for the end of the 1st Babylonian dynasty—i.e., 1595 BC.

Prior to this gap in the 2nd millennium BC, there is a period of five centuries with a well-established chronological structure. All the kings in the major city-states are known, as well as their sequence and the length of their reigns. Which sets of dates should be assigned to these reigns, however, depends on the date adopted for the 1st dynasty of Babylon. This period of five centuries extends from the beginning of the 3rd dynasty of Ur to the end of the 1st dynasty of Babylon—i.e., on the chronology adopted here, 2113–1595 BC. During this period the Babylonians dated their history not by regnal years but by the names of the years. Each year had an individual name, usually from an important event that had taken place in the preceding year. The lists of these names, called year lists or date lists, constitute as reliable a source in Babylonian chronology as the eponym lists do in Assyrian chronology. One of the events which almost invariably gave a name to the following year was the accession of a new king. Hence, the first full regnal year of a king was called “the year (after) NN became king.” In Assyria the number of personal names in an eponym list between the names of two successive kings normally equalled the number of years in the reign of the first king, and, similarly, in Babylonia the number of year names between two year names of the above kind nearly always equalled the number of years in the reign of the first king. Just as in Assyria, the eponym lists are almost certainly the source of the king lists, so in Babylonia the king lists are based on the year lists. Several of these king lists, compiled at a time when the year lists were still in use, survive. One gives the 3rd dynasty of Ur and the dynasty of Isin; another gives the dynasty of Larsa. Both may be school texts.

The 3rd dynasty of Ur and the dynasty of Isin also figure in the Sumerian king list, which reaches far back into the Sumerian period. The original version probably ended before the 3rd dynasty of Ur, but later scribes brought it up to date by adding that dynasty as well as the dynasty of Isin.

Jewish

The era at present in vogue among the Jews, counted from the creation of the world (anno mundi; abbreviated to AM), came into popular use about the 9th century AD. Traceable in dates recorded much earlier, this era has five styles conventionally indicated by Hebrew letters used as numerals and combined into mnemonics, which state the times of occurrence of the epochal mean conjunctions of moladim (see calendar: The Jewish calendar) or the orders of intercalation in the 19-year cycle or both. The respective epochs of these styles fall in the years 3762–3758 BC, inclusive. By about the 12th century AD the second of the mentioned styles, that which is in use at present, superseded the other styles of the era anno mundi.

The styles of this era arise from variations in the conventional rabbinical computation of the era of the creation. This computation, like hundreds of other calculations even more variable and no less arbitrary, is founded on synchronisms of chronological elements expressed in the terms of biblical and early postbiblical Jewish eras.

The biblical era anno mundi underlies the dating of events (mainly in the book of Genesis) prior to the Exodus from Egypt. This period of biblical chronology abounds in intractable problems caused by discrepancies between the Jewish and Samaritan Hebrew texts and the Greek version known as the Septuagint, by apparent inconsistencies in some of the synchronisms, and by uncertainties about the method of reckoning.

During the period from the Exodus to the founding of Solomon’s Temple, the only continuous biblical era (chiefly in the remaining books of the Pentateuch) is the era of the Exodus. With regard to a crucial date expressed in this era—“In the four hundred and eightieth year after the people of Israel came out of the land of Egypt, in the fourth year of Solomon’s reign over Israel, in the month of Ziv, which is the second month, he began to build the house of the Lord” (I Kings 6:1)—there is again a discrepancy between the Hebrew text and the Septuagint. Other problems to be met with during this period are due to the obscurity of chronological data in the book of Judges and in I and II Samuel.

During the following period, the Bible uses the eras of the regnal years of monarchs (the kings of Judah, Israel, and Babylon) and of the Babylonian Exile. This period of biblical chronology likewise poses numerous problems, also the result of apparent inconsistencies of the synchronisms—e.g., in the period from the accession of Rehoboam of Judah and of Jeroboam of Israel to the fall of Samaria “in the sixth year of Hezekiah [of Judah], which was the ninth year of Hoshea king of Israel” (II Kings 18:10) the reigns of the southern kingdom exceed those of the northern kingdom by 25 years.

The biblical data might be easier to harmonize if the occurrence of coregencies were assumed. Yet, as an ever-variable factor, these evidently would not lead to the determination of the true chronology of this period. Scholars therefore seek additional information from sources outside the Bible—e.g., inscriptions on Assyrian monuments, which are dated by the so-called eponym lists. Substantial use also has been made of the data in the king list known as Ptolemy’s Canon (compiled in the 2nd Christian century) commencing in 747 BC with the reigns of the Babylonian kings (see above Babylonian and Assyrian). Scholars differ widely, however, in their interpretation of details, and numerous chronological problems remain unsolved. Only a few dates in this period can be fixed with any degree of confidence.

After the Babylonian Exile, as evidenced by the data in the Bible and the Aswān papyri, the Jews reckoned by the years of the Persian kings. The chronological problems of this period are caused by the apparent disorder in the sequence of events related in the biblical books of Ezra and Nehemiah and by the difficulty of identifying some of the Persian kings in question. For example, the King Artaxerxes of these books may stand for Artaxerxes I Longimanus (465–425 BC), for Artaxerxes II Mnemon (404–359/358 BC), or in the case of Ezra at any rate, for Artaxerxes III Ochus (359/358–338/337 BC).

From the Grecian period onward, Jews used the Seleucid era (especially in dating deeds; hence its name Minyan Sheṭarot, or “Era of Contracts”). In vogue in the East until the 16th century, this was the only popular Jewish era of antiquity to survive. The others soon became extinct. These included, among others, national eras dating (1) from the accession of the Hasmonean princes (e.g., Simon the Hasmonean in 143/142 BC) and (2) from the anti-Roman risings (“era of the Redemption of Zion”) in the years 66 and 131 of the Common (Christian) Era. Dates have also been reckoned from the destruction of the Second Temple (le-ḥurban ha-Bayit). The various styles of the latter, as also of the Seleucid era and of the era anno mundi, have often led to erroneous conversions of dates. The respective general styles of these eras correlate as follows: 3830 AM = year 381 of the Seleucid era = year 1 of the Era of the Destruction = year 69/70 of the Common (Christian) Era.

The earliest Jewish chronologies have not survived. Of the work of the Alexandrian Jew Demetrius (3rd century BC), which deduced Jewish historical dates from the Scriptures, only a few fragments are extant. In the Book of Jubilees, events from the creation to the Exodus are dated in jubilee and sabbatical cycles of 49 and 7 years, respectively. Scholars differ as to the date and origin of this book. The era of the creation therein is unlikely to have been other than hypothetical.

The earliest and most important of all Jewish chronologies extant is the Seder ʿolam rabbaʾ (“Order of the World”), transmitted, according to Talmudic tradition, by Rabbi Yosi ben Halafta in the 2nd century AD. The author was possibly the first to use the rabbinic Era of the Creation. His chronology extends from the creation to Bar Kokhba in the days of the Roman emperor Hadrian (2nd century AD); but the period from Nehemiah to Bar Kokhba (i.e., from Artaxerxes I or II to Hadrian) is compressed into one single chapter. The Persian phase shrinks to a mere 54 years. The smaller work Seder ʿOlam zuṭaʾ completes the Rabbaʾ. It aims to show the Babylonian exilarchs as lineal descendants of David.

Megillat taʿanit (“Scroll of Fasting”), although recording only the days and months of the year without the dates of the years, is nevertheless an important source for Jewish chronology. It lists events on 35 days of the year that have been identified with events in five chronological periods: (1) pre-Hasmonean, (2) Hasmonean, (3) Roman (up to AD 65), (4) the war against Rome (65–66), and (5) miscellaneous. The authors, or rather the last revisers, are identified with Zealots guided by Hananiah ben Hezekiah ben Gurion and his son Eliezer.

Greek

As the cities of ancient Greece progressed to their classical maturity, the need arose among them for a chronological system on a universally understood basis. In the archaic period, genealogies of local monarchs or aristocrats sufficed for the historical tradition of a given area, and events were associated with the lifetimes of well-known ancestors or “heroes.” The synoikismos (founding of the united city) of Athens took place “in the time of Theseus”; the Spartan ephorate (chief magistracy) was established “in the reign of King Theopompus.” When the city-states adopted annual magistracies, the years were designated by the eponymous officials—“in the archonship of Glaucippus” or “when Pleistolas was ephor.” This was the local usage throughout classical and Hellenistic Greece, the title of the magistrate varying in different cities. Sometimes tenure of a priesthood provided the chronological basis, as at Argos, where years were dated as the nth of the (named) priestess of Hera. The correctness of the series was a matter first of memory and later of careful record. The list of annual archons at Athens was known back to 683 BC (in modern terms). Lists of dynasties also amounted to recorded folk memory, and in all genealogical reckoning there is a point, for modern critics, at which acceptable tradition shades into myth. Corruption of the records was introduced through error or political design, and traditions often conflicted.

Chronology became subject to systematization when cities felt a national need for accurate clarification of their past. In literature the growth of historiography initiated a search for a method of dating that could be universally applied and acknowledged. In the 5th and 4th centuries, local historians used local magistracies as their framework; research was devoted to rationalization of conflicting traditions and production of definitive lists. Charon of Lampsacus, perhaps in the early 5th century, compiled a record of Spartan magistrates; Hellanicus of Lesbos, author of the earliest history of Athens, wrote on the priestesses of Argos. Lists of victors in the great Olympic games were valid for all Greece, pointing the way to the widely accepted reckoning by Olympiads. The Athenian Philochorus was the latest (early 3rd century BC) of compilers of Olympionikai.

The 5th-century historian Herodotus relied for his chronology principally upon the reckoning by generations used by his informants, conventionally accepted as showing three generations to a century. In some cases a 40-year, or other, reckoning was used, and varying traditions sometimes produced difficulty of synchronism. Thucydides, writing “contemporary” history, recognized the chronological problems involved. He dated the beginning of the Peloponnesian War by the Athenian, Spartan, and Argive systems and thenceforward marked the passage of time by seasonal indications. Synchronization was not helped by the fact that the official year began at different times in different cities. In later historical writing the impossibility of accurately coordinating the Athenian and Roman years resulted in serious chronological difficulties.

The system of dating by Athenian archons came to be recognized outside Attica as of wider value, but, in the Hellenistic period, Alexandrian scholarship, represented especially by Eratosthenes of Cyrene, the “father of chronology,” was instrumental in promoting the use of the Olympiads as an acceptable system, reckoning a four-year period from each celebration of the Olympic Games. Timaeus of Tauromenium (c. 356–260 BC) was the first historian to employ it, but it was little used outside historical writing. Aristotle had been concerned to identify the generation of the first Olympiad, accepted as 776 BC on modern reckoning. For convenience, the beginning of the Olympic year was equated with the summer solstice, when the Athenian year also began. This makes it generally necessary for a Greek year to receive a double date in modern terms (e.g., the death of the philosopher Epicurus in 271/270 BC). Eratosthenes’ system produced tables of dates, from which, for example, the fall of Troy could be dated to 1184/83 BC. The “Parian Marble” of 264/263 BC is an inscribed record of events from the time of Cecrops, first king of Athens, reckoning years between the date of the inscription, fixed by the Athenian archon, and each event concerned. Some cities inscribed lists of their eponymous magistrates; the Athenians were the first to do so c. 425 BC. A list from Sicilian Tauromenium originally spanned some 300 years. The regnal years of the Hellenistic monarchs or the count from a fixed event (a city foundation or refoundation) also provided acceptable chronological reckoning often useful for more than contemporary or local purposes.

The use of these chronological possibilities is best seen in historians using the annalistic method, of whom Diodorus Siculus is most notable. In the Christian period, Eusebius, followed by St. Jerome, began the work of reconciling all these indications to the Judaic tradition and produced the foundation of chronology in terms of the Julian calendar upon which modern historians have constructed their framework.

For modern scholarship the problem, in E.J. Bickerman’s words, is “how we know Caesar was assassinated on March 15, 44 BC.” Before 480 BC, no date can be precise in terms of the Julian calendar unless confirmed by astronomical phenomena. Archaic chronology relies upon the typology of Corinthian pottery in relation to the foundation dates for Greek colonies in Sicily implicit in Thucydides, book vi. Julian dates given for this period (e.g., for the tyranny of Peisistratus in Athens) stem from a complex combination of ancient chronographic tradition with modern archaeology, acceptable only with appropriate reserve. Literary tradition gives the succession of Athenian archons from 480 to 294 BC. The regnal, era, and Olympiad years also provide dates within a 12-month period. Closer dating is seldom possible unless the sources give precise information in calendric terms, as occasionally in literature and regularly in Athenian and Egyptian public documents. Even these are not translatable into Julian months and days unless coordinated with knowledge of contemporary solar or lunar phenomena and of possible official interference with the calendar.

Roman

The establishment of a sound chronology for Roman history, as for Greek, depends on the assessment of the evidence available, which falls into two categories—literary and archaeological.

Literary evidence

Although by the late 3rd century BC the Greek mathematician Eratosthenes was working on the systematization of chronography and a series of learned historians had used the documentary method—e.g., for Roman history, Timaeus of Tauromenium, to whom are probably due many of the synchronizations of Roman history with the Greek Olympiads—unfortunately this tradition of documentation and concern for chronology did not immediately pass over into Roman historiography. According to Cicero in De oratore, the earliest Roman historians did no more than “compile yearbooks”—for example, Fabius Pictor in the late 3rd century BC, Lucius Calpurnius Piso in the 2nd, and the so-called Sullan annalists in the 1st. Of these authors it is possible to judge only at second hand, and only those of the 1st century were much used directly by the historians whose work survives in any quantity, notably Livy, Dionysius of Halicarnassus, and Diodorus Siculus. In these authors, as in other 1st-century historians such as Sallust, there is little concept of documentation or research other than comparison of literary sources; for none was chronology a direct concern, and in many cases dramatic effectiveness took priority over fidelity to truth. Apart from the Greek Polybius, who treated the rise of Roman power in the Mediterranean from 264 to 146 BC, it was not until Cicero’s time that the conception of historical scholarship developed in Rome. Cicero’s friend Atticus not only was concerned to draw up a chronological table in his Liber annalis but had undertaken research to that end, and the great scholar Marcus Terentius Varro and a little later the learned Marcus Verrius Flaccus produced a vast body of erudite work, nearly all lost. To this source must probably be ascribed the Fasti Capitolini, a list of magistrates from the earliest republic to the contemporary period, set up near the regia (the office and archive of the pontifices, or high priests), perhaps on the adjacent Arch of Augustus, at the end of the 1st century BC. This work, since it is based on inscriptions, is sometimes given precedence over literary evidence, but, since it is a compilation, it is still subject to serious error.

Sources used by Roman historians

The traditionally early extant bodies of law, such as the Twelve Tables from the early republic, were of little chronological value, and juristic commentarii were liable to mislead through their zeal for precedent, while Cicero, in spite of Polybius’ claim to have inspected early treaties preserved in the Capitol definitely states that there were no public records of early laws. A source frequently referred to is the Annales maximi, a collection made about 130 BC of the annual notices displayed on a white board by the pontifices and containing notes of food prices, eclipses, etc. Dionysius of Halicarnassus implied that they gave a date for the foundation of the city but was reluctant to accept their authority; and one of the eclipses is referred to by Cicero as being mentioned also by Ennius, but unfortunately the number of the year “from the foundation of the city” is corrupt in the text. Although it is possible to calculate the dates of eclipses astronomically in terms of the modern era, it is difficult to link these to Roman chronology because of the uncertainty of the figures and because of the confused state of the Roman calendar before the Julian reform (see calendar: The early Roman calendar). Another difficulty is that the early records may have been burned in 390 BC when Celtic tribes sacked the city; also they would probably have been largely unintelligible if authentic.

Livy quoted the 1st-century annalist Gaius Licinius Macer as having found in the temple of Juno Moneta “linen rolls” giving lists of magistrates; but he also said that Macer and Quintus Aelius Tubero both cited the rolls for the consuls of 434 but gave different names. In any case, it is unlikely that the list could have been older than the temple, which dates from 344 BC. It is clear that the chief sources for the lists were the pedigrees of prominent Roman families, such as the Claudii Marcelli, Fabii, and Aemilii, drawn up by Atticus; but Cicero and Livy agree that tendentious falsifications had in many cases corrupted the records, and other suspicious facts are the appearance of obviously later or invented cognomina, or third names, and of plebeian gentile names for the earliest period, when only patricians bore them. Many scholars, however, accept the general authenticity of the lists—one reason being the appearance in them of extinct patrician families—but prefer Livy’s version to that of the Capitoline lists, which show signs of late revision, often give names in incorrect order, and contain other anomalies.

The question, therefore, remains whether Roman chronography was dependent on the lists of magistrates or whether these were adapted to fit other known datings. The apparent advantages of the existence of a terminal date, the “foundation of the city,” is illusory for Roman chronology, since it depended on back reckoning and was not agreed even in antiquity. Various ancient scholars each assumed a different date. Each computed his date by adding a different number of years of kingly rule from the foundation of the city to his estimate of the date of the foundation of the republic. This, in turn, was presumably computed by counting back over the yearly lists of magistrates. There may have been traditions about the intervals between certain events in early Roman history, but the frequently accepted reckoning of 244 years of kingly rule seems to be a calculation based only on the conventional 35-year generation for the rule of the seven legendary kings. Polybius claimed that the dating of the first republican consulship to 508/507 BC could be substantiated by an extant copy of a contemporary treaty. Combined with the traditional kingly period, this would give a foundation date of 751–750, reckoned inclusively, and 752–751, exclusively (Cato’s date). The chronological scheme worked out by Varro added two years of nonconsular rule, thus the foundation of Rome was put in 754/753 and the beginning of the republic in 510/509. Varro’s dates became standard for later Romans and are sometimes also used by modern scholars in a purely conventional sense. But it remains uncertain whether the dating depended on the magistrate lists or whether these were “doctored” to synchronize with given dates or intervals, whether these were traditional or calculated in some other way. Anomalies such as Livy’s five-year anarchy 15 years after the Gallic invasion, Diodorus’ repetition of magistrates’ names, and the “dictator years” in the lists are perhaps attempts to synchronize the various pedigrees.

Contribution of archaeology

Archaeology can provide many dates useful to the detailed study of Roman history, especially from coins and inscriptions, but, for the general scheme of early chronology, its value is largely negative. It shows, for example, that Rome evolved over a lengthy period and was not really “founded,” though a “foundation” date might perhaps refer to the first common celebration of the Septimontium, or festival of the seven hills; again, if that dating is dependent on the seven kings, archaeology shows that the tradition about them, though it may preserve genuine names and events, is largely legendary.

Datings after the 1st century BC

In this better documented period, datings to consul years, or later to the years of tribunician power of the emperors, are normally intelligible, despite a few notorious cruxes, although up to the Julian reform the state of the calendar has always to be taken into account. In parts of the empire, however, different eras were used—e.g., that of the Seleucids—and from the 4th century AD dates were often calculated in terms of the years of the indiction, a 15-year cycle connected with the levying of taxes, a method that continued in use for many centuries in spite of difficulties, such as lack of synchronization among the various provinces.

Christian

The Christian Era is the era now in general use throughout the world. Its epoch, or commencement, is January 1, 754 AUC (ab urbe condita—“from the foundation of the city [of Rome]”—or anno urbis conditae—“in the year of the foundation of the city”). Christ’s birth was at first believed to have occurred on the December 25 immediately preceding. Years are reckoned as before or after the Nativity, those before being denoted BC (before Christ) and those after by AD (anno Domini, “in the year of the Lord”). Chronologers admit no year zero between 1 BC and AD 1. The precise date of commencing the annual cycle was widely disputed almost until modern times, December 25, January 1, March 25, and Easter day each being favoured in different parts of Europe at different periods.

The Christian Era was invented by Dionysius Exiguus (c. AD 500–after 525), a monk of Scythian birth resident in Italy; it was a by-product of the dispute that had long vexed the churches as to the correct method of calculating Easter. Many churches, including those in close contact with Rome, followed 95-year tables evolved by Theophilus, bishop of Alexandria, and by his successor, St. Cyril; but some Western churches followed other systems, notably a 532-year cycle prepared for Pope Hilarius (461–468) by Victorius of Aquitaine. In 525, at the request of Pope St. John I, Dionysius Exiguus prepared a modified Alexandrian computation based on Victorius’ cycle. He discarded the Alexandrian era of Diocletian, reckoned from AD 284, on the ground that he “did not wish to perpetuate the name of the Great Persecutor, but rather to number the years from the Incarnation of Our Lord Jesus Christ.”

Somehow Dionysius reckoned the birth of Christ to have occurred in 753 AUC; but the Gospels state that Christ was born under Herod the Great—i.e., at the latest in 750 AUC. Dionysius’ dating was questioned by the English saint Bede in the 8th century and rejected outright by the German monk Regino of Prüm at the end of the 9th. Nevertheless, it has continued in use to the present day, and, as a result, the Nativity is reckoned to have taken place before the start of the Christian Era.

The new chronology was not regarded as a major discovery by its author; Dionysius’ own letters are all dated by the indiction (see below). The use of the Christian Era spread through the employment of his new Easter tables. In England the Christian Era was adopted with the tables at the Synod of Whitby in 664. But it was the use, above all by Bede, of the margins of the tables for preserving annalistic notices and the consequent juxtaposition of historical writing with calendrical computations that popularized the new era. Outside Italy it is first found in England (in a charter of 676) and shortly afterward in Spain and Gaul. It was not quickly adopted in royal diplomas and other solemn documents, however, and in the papal chancery it did not replace the indiction until the time of John XIII (965–972). The Christian Era did not become general in Europe until the 11th century; in most of Spain it was not adopted until the 14th and in the Greek world not until the 15th.

Of the alternative chronologies used by Christians, the most important were: (1) the indiction, (2) the Era of Spain, and (3) the Era of the Passion. The indiction was a cycle of 15 years originally based on the interval between imperial tax assessments but during the Middle Ages always reckoned from the accession of Constantine, in 312. Years were given according to their place in the cycle of 15, the number of the indiction itself being ignored. This chronology was the most widespread in the early Middle Ages, but its use diminished rapidly in the 13th century, although public notaries continued to use it until the 16th. The Era of Spain was based on an Easter cycle that began on January 1, 716 AUC (38 BC), marking the completion of the Roman conquest of Spain. First recorded in the 5th century, it was in general use in Visigothic Spain of the 6th and 7th centuries and, after the Arab invasions, in the unconquered Christian kingdoms in the north of the Iberian Peninsula. It was abolished, in favour of the Era of the Incarnation, in Catalonia in 1180, in Aragon in 1350, in Castile in 1383, and in Portugal in 1422. The Era of the Passion, commencing 33 years after that of the Incarnation, enjoyed a short vogue, mainly in 11th-century France.

Muslim

Unlike earlier chronological systems in use before Islam, Islamic chronology was instituted so soon after the event that was to be the beginning of the Muslim era that no serious problems were encountered in its application. According to the most reliable authorities, it was ʿUmar I, the second caliph (reigned 634–644), who introduced the era used by the Muslim world. When his attention was drawn by Abū Mūsā al-Ashʿarī to the fact that his letters were not dated, ʿUmar consulted with men at Medina and then ordered that the year of the Hijrah (Hegira), the Prophet’s flight from Mecca to Medina, be taken as the beginning of an era for the Muslim state and community. According to the Muslim calendar, the Hijrah took place on 8 Rabīʿ I, which corresponds to September 20, 622 (AD), in the Julian calendar. But, as Muḥarram had been already accepted as the first month of the lunar year, ʿUmar ordered that (Friday) 1 Muḥarram (July 16, 622) be the beginning of the reckoning. It is generally accepted that this was done in AH 17 (anno Hegirae, “in the year of the Hijrah”).

There are a few points in connection with this that deserve mention: first, there is no real agreement on the exact date of the Hijrah—other dates given include 2 and 12 Rabīʿ I; second, the year in which ʿUmar issued the order is a point of contention—the years 16 and 17 are sometimes given; third, some people have ascribed the use of the chronology to the Prophet himself. According to some sources, the Hijrah date was first used by Yaʿlā ibn Umayyah, Abū Bakr’s governor in Yemen. This sounds somewhat plausible because Yemenis were probably used to affixing dates to their documents. There is, however, a consensus among workers in the field that 8 Rabīʿ I was the day of the Hijrah, that ʿUmar instituted the use of the date for the new era, and that this was done in AH 17. The choice of the Hijrah as the beginning of the epoch has two reasons. On the one hand, its date had been fixed; on the other, ʿUmar and his advisers must have recognized the importance of the migration—Islam had become, as a result, a religion and a state.

Before the introduction of the new epoch, the Arabs had been acquainted with chronologies used by their neighbours, the Seleucids and the Persians. In Yemen the practice of dating had been perfected to the extent that inscriptions show the day, the month, and the year. In Mecca the “year of the Elephant,” supposedly coinciding with the birth of the Prophet, had been in use. For the period between the migration and the institution of the new epoch, the Muslims of Medina resorted to naming the year after local events—“the year of the order of fighting” and “the year of the earthquake,” etc.

The lunar year was adopted by the Muslims for the new chronology. In this there was hardly any innovation insofar as Arabia was concerned.

The chronology introduced by ʿUmar was adopted throughout the Muslim world, although earlier epochs continued in use in outlying provinces. Muslim historians, annalists, and chroniclers met with difficulties when writing their books on pre-Islamic history. No practice had as yet developed for pre-Hijrah dating; therefore, when writing about the history of various lands in pre-Islamic times, authors resorted to the use of chronologies previously in existence there (e.g., Persian, Indian, Seleucid, Alexandrian). For the histories of the area under Islam, writers used only Muslim chronology, while non-Muslim authors (e.g., Bar Hebraeus) used the Seleucid and the Hijrah dates when discussing events pertaining to provinces that had been Byzantine and therefore still had fairly large groups of Christians.

The era of the Hijrah is in official use in Saudi Arabia, Yemen, and in the Persian Gulf area. Egypt, Syria, Jordan, Morocco, Algeria, Libya, and Tunisia use both the Muslim and the Christian eras. Many Muslim countries, such as Turkey, Nigeria, and Pakistan, use the Christian Era.

Within the general uniformity of applying the Hijrah era proper, there existed differences, some of which were the result of earlier pre-Islamic practices; others were the result of continuous contacts of Muslim countries with their European neighbours, with whom they had economic as well as political relations. An example of the former was the work of the ʿAbbāsid caliph al-Muʿtaḍid, who brought the Nowrūz (Persian New Year’s Day) back to date in keeping with the agricultural activities of the community. Maḥmūd Ghāzān introduced the Khānian era in Persia in AH 701, which was a reversion to the regnal chronologies of antiquity. It continued in use for some generations, then the ordinary Hijrah era was reintroduced. A similar step was taken by Akbar when he established the Ilāhī era, which began on Rabīʿ II 963 (February 13, 1556), the date of his accession; the years were solar.

Two Muslim countries, Turkey and Iran, introduced more drastic changes into their chronology because of European influences.

In Turkey the Julian calendar was adopted in AH 1088 (AD 1676–77) and used solar months with Hijrah dating. The year was officially called the Ottoman fiscal year but was popularly known as the marti year, after mart (Turkish for March), which was the beginning of the year. Under Mustafa Kemal Atatürk, the Gregorian calendar and the Christian Era were officially adopted in Turkey (1929). Iran also adopted a solar year; the names of the months in its calendar are Persian, and the era is still that of the Hijrah.

[admin]

Pataliputra
by Wikipedia
Accessed: 6/26/21

-- Patala [Pattala], by Laxman Burdak, IFS (Retd.)
-- Patiala, by Wikipedia
-- Patali, Anbarabad [Iran], by Wikipedia
-- Patala, by Wikipedia
-- Pataliputra, by Wikipedia

1658 Jansson Map of the Indian Ocean (Erythraean Sea)
Erythraei Sive Rubri Maris Periplus. Olim Ab Arriano Descriptus. Nunc Vero ab Abrah. Ortelio Ex Eodem Delineatus. [Google Translate: Erythraei or red sea periplus. Once the Arrian described. But now from Abraham. Ortelius the same project.]


Palibothra

The jurisprudence of the Hindus and Arabs being the field which I have chosen for my peculiar toil, you cannot expect that I should greatly enlarge your collection of historical knowledge; but I may be able to offer you some occasional tribute; and I cannot help mentioning a discovery which accident threw in my way, though my proofs must be reserved for an essay which I have destined for the fourth volume of your Transactions. To fix the situation of that Palybothra (for there may have been several of the name) which was visited and described by Megasthenes, had always appeared a very difficult problem, for though it could not have been Prayaga, where no ancient metropolis ever stood, nor Canyacubja, which has no epithet at all resembling the word used by the Greeks; nor Gaur, otherwise called Lacshmanavati, which all know to be a town comparatively modern, yet we could not confidently decide that it was Pataliputra, though names and most circumstances nearly correspond, because that renowned capital extended from the confluence of the Sone and the Ganges to the site of Patna, while Palibothra stood at the junction of the Ganges and Erannoboas, which the accurate M. D'Ancille had pronounced to be the Yamuna; but this only difficulty was removed, when I found in a classical Sanscrit book, near 2000 years old, that Hiranyabahu, or golden armed, which the Greeks changed into Erannoboas, or the river with a lovely murmur, was in fact another name for the Sona itself; though Megasthenes, from ignorance or inattention, has named them separately. This discovery led to another of greater moment, for Chandragupta, who, from a military adventurer, became like Sandracottus the sovereign of Upper Hindustan, actually fixed the seat of his empire at Pataliputra, where he received ambassadors from foreign princes; and was no other than that very Sandracottus who concluded a treaty with Seleucus Nicator; so that we have solved another problem, to which we before alluded, and may in round numbers consider the twelve and three hundredth years before Christ, as two certain epochs between Rama, who conquered Silan a few centuries after the flood, and Vicramaditya, who died at Ujjayini fifty-seven years before the beginning of our era.

-- Discourse X. Delivered February 28, 1793, P. 192, Excerpt from "Discourses Delivered Before the Asiatic Society: And Miscellaneous Papers, on The Religion, Poetry, Literature, Etc. of the Nations of India", by Sir William Jones

-- Discovery of the Exact Site of Asoka's Classic Capital of Pataliputra, The Palibothra of the Greeks, and Description of the Superficial Remains, by L.A. Waddell, M.B., 1892
-- Report on the Excavations At Pataliputra (Patna): The Palibothra of the Greeks, by L.A. Waddell

Plan of Pataliputra compared to present-day Patna
Pataliputra is located in India

Alternative name Pātaliputtā (Pāli)
Location Patna district, Bihar, India
Region South Asia
Coordinates 25°36′45″N 85°7′42″ECoordinates: 25°36′45″N 85°7′42″E
Altitude 53 m (174 ft)
Length 14.5 km (9.0 mi)
Width 2.4 km (1.5 mi)
History
Builder Ajatashatru
Founded 490 BCE
Abandoned Became modern Patna
Associated with Haryankas, Nandas, Mauryans, Shungas, Guptas, Palas, Sher Shah Suri
Management Archaeological Survey of India

Pataliputra (Sanskrit: पाटलिपुत्र) (IAST: Pāṭaliputra), adjacent to modern-day Patna, was a city in ancient India, originally built by Magadha ruler Udayin in 490 BCE as a small fort (Pāṭaligrāma) near the Ganges river.[1]

It became the capital of major powers in ancient India, such as the Shishunaga Empire (c. 413–345 BCE), Nanda Empire (c. 460 or 420–325 BCE), the Maurya Empire (c. 320–180 BCE), the Gupta Empire (c. 320–550 CE), and the Pala Empire (c. 750–1200 CE). During the Maurya period (see below), it became one of the largest cities in the world. As per the Greek diplomat, traveler and historian Megasthenes, during the Mauryan Empire (c. 320–180 BCE) it was among the first cities in the world to have a highly efficient form of local self government.[2] Afterwards, Sher Shah Suri (1538–1545) revived Pataliputra, which had been in decline since the 7th century CE, and renamed it Paṭna.

As an ambassador


According to Arrian, Megasthenes lived in Arachosia and travelled to Pataliputra.

Distance from Helmand, Afghanistan to Patna, India = 2505 km. = 1556 miles, 508 hrs walking = 63 days @ 8 hrs./day.

Megasthenes was a Greek ambassador of Seleucus I Nicator in the court of Chandragupta Maurya. Arrian explains that Megasthenes lived in Arachosia, with the satrap Sibyrtius, from where he visited India.

-- Megasthenes, by Wikipedia

The location of the site was first identified in modern times in 1892 by Laurence Waddell, published as Discovery Of The Exact Site Of Asoka's Classic Capital.[3] Extensive archaeological excavations have been made in the vicinity of modern Patna.[4][5] Excavations early in the 20th century around Patna revealed clear evidence of large fortification walls, including reinforcing wooden trusses.[6][7]

-- Discovery of the Exact Site of Asoka's Classic Capital of Pataliputra, The Palibothra of the Greeks, and Description of the Superficial Remains, by L.A. Waddell, M.B., 1892

-- Report on the Excavations At Pataliputra (Patna): The Palibothra of the Greeks, by L.A. Waddell

Etymology

The etymology of Pataliputra is unclear. "Putra" means son, and "pāṭali" is a species of rice or the plant Bignonia suaveolens.[8] One traditional etymology[9] holds that the city was named after the plant.[10] Another tradition says that Pāṭaliputra means the son of Pāṭali, who was the daughter of Raja Sudarshan.[11] As it was known as Pāṭali-grāma ("Pāṭali village") originally, some scholars believe that Pāṭaliputra is a transformation of Pāṭalipura, "Pāṭali town".[12] Pataliputra was also called Kusumapura (city of flowers).

Pataligram to Patna -- The Historical Journey Of The 'City of Flowers'

The cities, towns or villages that once occupied the site of modern Patna had carried quite a large number of names in different periods of history and most of them were in the name of 'FLOWERS.' The earliest to exist at the site seems to have been a small sprawling village with the name of Patali, Pataligrama, Padali or Padalipura as mentioned in Buddhist and Jain traditions.

What Does Megasthenes Say About The Kings Who Ruled?

1. He calls Sandracottus the king of the Prassi and he mentions the names of Xandramus as predecessor and Sandrocyptus as successor to Sandracottus. There is absolutely no resemblance in these names to Bindusara (the successor to Chandragupta Maurya) and Mahapadma Nanda, the predecessor.

2. He makes absolutely no mention of Chanakya or Vishnugupta, the Acharya who helped Chandragupta ascend the throne.

3. He makes no mention of the widespread presence of the Baudhik or Sramana tradition [Rishi tradition] during the time of the Maurya empire.

4. He claims the capital is Palimbothra or Palibothra, and that the city exists near the confluence of the Ganga and the Eranaboas (Hiranyabahu). But the Puranas are clear that all the 8 dynasties after the Mahabharata war had their capital at Girivraja (Rajagriha), located in the foothills of the Himalayas. There is no mention of Pataliputra in the Puranas. So, the assumption made by Sir William that Palimbothra is Pataliputra has no basis in fact and is not attested by any piece of evidence. If the Greeks could pronounce the first P in (Patali) they could certainly have pronounced the second p in Putra, instead of bastardising it as Palimbothra. Granted the Greeks were incapable of pronouncing any Indian names, but there is no reason why they should not be consistent in their phonetics.

5. The empire of Chandragupta was known as Magadha Empire. It had a long history even at the time of Chandragupta Maurya. In Indian literature, this powerful empire is amply described by its name but the same is absent in Greek accounts. It is difficult to understand as to why Megasthenes did not use this name “Magadha” and instead used the word Prassi, which has no equivalent or counterpart in Indian accounts.

-- Historical Dates From Puranic Sources, by Prof. Narayan Rao

Vayupurana mentions the name of Pataliputra as Kusumapura. In Tattvarthasutra of Umasvati, a celebrated Jain Author who lived here in the first-second centuries A.D., the place is described as Kusumapura. It literally means a 'city of flowers.' Gargi-Samhita names Pataliputra as Kusum-Dhvaja or Pushpapura -- variant of Kusumapura. The modern name of Phulwarisharif of a small hamlet near Patna is obviously a survival of the ancient name. One tradition says that in the time of Nandas, the name was Padmawati. It is under the Mauryans that the name of Pataliputra came in common use. Megasthenes, the Greek ambassador, at the court of Chandragupta Maurya, mentioned Pataliputra with the Greek utterance of 'Palibothra.' The celebrated Buddhist monk, Hiuen-Tsang who came to India in the seventh century A.D., also knew it by the name of Pataliputra.

-- The Wonder That Was Pataliputra, by brandingbihar.com

"O World-Honoured One! To the east, beyond worlds as numerous as the sands of 20 Ganges, is a world called "Acala"....The rivers contain various flowers, such as the utpala, padma, kumuda, pundarika, the fragrant, the greatly fragrant, the wonderfully fragrant, the nitya, and the bloom that unhinderedly protects all beings. Also, on both banks are numerous flowers, such as the atimuktaka, campaka, pataliputra, varsika, mallika, mahamallika, simmallika, sumana, yukthika, dhanika, nitya, and the bloom that unhinderedly protects all beings.

-- The Mahayana Mahaparinirvana Sutra, Translated into English by Kosho Yamamoto, from Dharmakshema’s Chinese version, 1973

"Karavira, Jati, Champaka, Lotus, and Patali, are the five flowers (275)."

-- Mahanirvana Tantra: Tantra of the Great Liberation, Translated by Arthur Avalon (Sir John Woodroffe)

History

There is no mention of Pataliputra in written sources prior to the early Jain and Buddhist texts (the Pali Canon and Āgamas), where it appears as the village of Pataligrama and is omitted from a list of major cities in the region.[13] Early Buddhist sources report a city being built in the vicinity of the village towards the end of the Buddha's life; this generally agrees with archaeological evidence showing urban development occurring in the area no earlier than the 3rd or 4th Century BCE.[13] In 303 BCE, Greek historian and ambassador Megasthenes mentioned Pataliputra as a city in his work Indika.[14]Diodorus, quoting Iambulus mention that the king of Pataliputra had a "great love for the Greeks".[15]

The city of Pataliputra was formed by fortification of a village by Haryanka ruler Ajatashatru, son of Bimbisara.[16]

Its central location in north eastern India led rulers of successive dynasties to base their administrative capital here, from the Nandas, Mauryans, Shungas and the Guptas down to the Palas.[17] Situated at the confluence of the Ganges, Gandhaka and Son rivers, Pataliputra formed a "water fort, or jaldurga".[18] Its position helped it dominate the riverine trade of the Indo-Gangetic plains during Magadha's early imperial period. It was a great centre of trade and commerce and attracted merchants and intellectuals, such as the famed Chanakya, from all over India.

Two important early Buddhist councils are recorded in early Buddhist texts as being held here, the First Buddhist council immediately following the death of the Buddha and the Second Buddhist council in the reign of Ashoka. Jain and Brahmanical sources identify Udayabhadra, son of Ajatashatru, as the king who first established Pataliputra as the capital of Magadha.[13] The Sangam Tamil epic Akanaṉūṟu mentions Nanda kings ruling Pataliputra.[19][20][21]

Capital of the Maurya Empire


Ruins of pillared hall at Kumrahar site at Pataliputra.


The Pataliputra capital, discovered at the Bulandi Bagh site. 4th-3rd c. BCE.


Mauryan remains of a wooden palissade at Bulandi Bagh site.

During the reign of Emperor Ashoka in the 3rd century BCE, it was one of the world's largest cities, with a population of about 150,000–400,000.[22] The city is estimated to have had a surface of 25.5 square kilometers, and a circumference of 33.8 kilometers, and was in the shape of a parallelogram and had 64 gates (that is, approximately one gate every 500 meters).[23] Pataliputra reached the pinnacle of prosperity when it was the capital of the great Mauryan Emperors, Chandragupta Maurya and Ashoka. The city prospered under the Mauryas and a Greek ambassador, Megasthenes, resided there and left a detailed account of its splendour, referring to it as "Palibothra":

"Megasthenes says that on one side where it is longest this city extends ten miles in length, and that its breadth is one and three-quarters miles; that the city has been surrounded with a ditch in breadth 600 feet, and in depth 45 feet; and that its wall has 570 towers and 64 gates." - Arrian "The Indica"[24]

Mauryan remains of a wooden palisade discovered at the Bulandi Bagh site of Pataliputra.


Fa-Hien at the ruins of Ashoka's palace in Pataliputra in the 4th century CE (artist impression).

Strabo in his Geographia adds that the city walls were made of wood. These are thought to be the wooden palisades identified during the excavation of Patna.[25]

"At the confluence of the Ganges and of another river is situated Palibothra, in length 80, and in breadth 15 stadia. It is in the shape of a parallelogram, surrounded by a wooden wall pierced with openings through which arrows may be discharged. In front is a ditch, which serves the purpose of defence and of a sewer for the city." - Strabo, "Geographia"[26]

Aelian, although not expressly quoting Megasthenes nor mentioning Pataliputra, described Indian palaces as superior in splendor to Persia's Susa or Ecbatana:

"In the royal residences in India where the greatest of the kings of that country live, there are so many objects for admiration that neither Memnon's city of Susa with all its extravagance, nor the magnificence of Ecbatana is to be compared with them. (...) In the parks, tame peacocks and pheasants are kept." - Aelian in "De Natura Animalium"[27]

Under Ashoka, most of wooden structure of Pataliputra palace may have been gradually replaced by stone.[28] Ashoka was known to be a great builder, who may have even imported craftsmen from abroad to build royal monuments.[29] Pataliputra palace shows decorative influences of the Achaemenid palaces and Persepolis and may have used the help of foreign craftmen.[30] Which may be the result of the formative influence of craftsmen employed from Persia following the disintegration of the Achaemenid Empire after the conquests of Alexander the Great.[31][32]

Capital of later dynasties

The city also became a flourishing Buddhist centre boasting a number of important monasteries. It remained the capital of the Gupta dynasty (3rd–6th centuries) and the Pala Dynasty (8th-12th centuries). When Faxian visited the city in 400 A.D, he found the people to be rich and prosperous; they practised virtue and justice.[33] He found that the nobles and householders of the city had constructed several hospitals in which the poor of all countries, the destitute, the crippled and the diseased can get treatment. They could receive every kind of help gratuitously. Physicians would inspect the diseases, and order them food, drink, and medicines.[34] The city was largely in ruins when visited by Xuanzang.[35] In a fanciful 1559 book about world geography, the Italian Caius Julius Solinus briefly mentions a powerful Indian kingdom of Prasia with a capital at Palibotra.[36] Afterwards, Sher Shah Suri made Pataliputra his capital and changed the name to modern Patna.

Structure


Ruins of Pataliputra at Kumhrar.

Though parts of the ancient city have been excavated, much of it still lies buried beneath modern Patna. Various locations have been excavated, including Kumhrar, Bulandi Bagh and Agam Kuan.

During the Mauryan period, the city was described as being shaped as parallelogram, approximately 2.5 kilometers (1.5 miles) wide and 15 kilometers (9 miles) long. Its wooden walls were pierced by 64 gates. Archaeological research has found remaining portions of the wooden palisade over several kilometers, but stone fortifications have not been found.[37]

Excavated sites of Pataliputra

• Kumhrar
• Bulandi Bagh
• Agam Kuan

As dynastic capital

Pataliputra served as the capital under various Indian dynasties


Pataliputra served as the capital of the Haryanka dynasty and the Shishunaga dynasty of Magadha.


Pataliputra served as the capital of the Nanda Empire.


Pataliputra served as the capital of the Maurya Empire.


Pataliputra served as the capital of the Shunga Empire.


Pataliputra served as the capital of the Gupta Empire.


Pataliputra served as the capital of the Pala Empire.

Main recovered artifacts


The Masarh lion, 3rd century BCE.


Lohanipur torso.


Portion of pillar, found in Pataliputra.


Pataliputra griffin statuette.


Winged griffin.


Pataliputra Yakshas, with Mauryan inscriptions.


Kumrahar coping stone with vines.


Pataliputra lotus motifs.


Polished pillar from Pataliputra.


Mason marks at the base of a pillar.[38]


Chariot wheel, Bulandi Bagh, Mauryan period.


Bulandi Bagh female statuette, Sunga period.


Buddhist railing, Sunga period.

See also

• India portal
• Azimabad
• Magadh
• Names of Patna
• History of Patna

References

1. Kulke, Hermann; Rothermund, Dietmar (2004), A History of India, 4th edition. Routledge, Pp. xii, 448, ISBN 978-0-415-32920-0.
2. Schwanbeck, E.A. (4 October 2008). Ancient India as described by Megasthenes and Arrian (First published 1657) (23 ed.). Bibliolife.
3. Discovery Of The Exact Site Of Asoka's Classic Capital, 1892
4. "Patna". Encyclopædia Britannica. Encyclopædia Britannica Online. Encyclopædia Britannica Inc., 2013. Web. 13 Dec. 2013 <"Patna | India". Archived from the original on 30 November 2011. Retrieved 30 January 2011.>.
5. "Heritage wall for Metro corridor plan". Archived from the original on 22 November 2016.
6. "A relic of Mauryan era". Archived from the original on 27 November 2017.
7. Valerie Hansen Voyages in World History, Volume 1 to 1600, 2e, Volume 1 pp. 69 Cengage Learning, 2012
8. Monier-Williams Sanskrit-English Dictionary: Pāṭali, "Archived copy". Archived from the original on 16 July 2011. Retrieved 20 July 2009. (a junior synonym of Stereospermum colais "View crop". Archived from the original on 22 July 2011. Retrieved 20 July 2009.)
9. Encyclopaedia of Religion and Ethics, p.677
10. Folklore, Vol. 19, No. 3 (30 September 1908), pp. 349–350 Archived 10 May 2018 at the Wayback Machine
11. The Calcutta Review Vol LXXVI (1883), p.218
12. Language, Vol. 4, No. 2 (June , 1928), pp. 101–105 Archived 10 May 2018 at the Wayback Machine
13. Sujato, Bhikkhu; Bhikkhu, Brahmali, "1.1.5", The Authenticity of the Early Buddhist Texts (PDF), Oxford Center for Buddhist Studies, archived from the original on 20 November 2017.
14. Tripathi, Piyush Kumar (16 July 2015). "Realty to broaden horizon". The Telegraph. Calcutta. Archived from the original on 16 July 2015.
15. DIODORUS SICULUS -LIBRARY OF HISTORY-Book II, 60
16. Sastri 1988, p. 11.
17. Thapar, Romilak (1990), A History of India, Volume 1, New Delhi and London: Penguin Books. Pp. 384, ISBN 978-0-14-013835-1.
18. The Pearson Indian History Manual, Pearson Education India, A94.
19. Kowmareeshwari (Ed.), S. (August 2012). Agananuru, Purananuru. Sanga Ilakkiyam (in Tamil). 3 (1 ed.). Chennai: Saradha Pathippagam. p. 251.
20. The Song of Songs and Ancient Tamil Love Poems: Poetry and Symbolism By Abraham Mariaselvam
21. Akanaṉūṟu Verses 261 and 265
22. Preston, Christine (2009). The Rise of Man in the Gardens of Sumeria: A Biography of L.A. Waddell. Sussex Academic Press. p. 49. ISBN 9781845193157.
23. Schlingloff, Dieter (2014). Fortified Cities of Ancient India: A Comparative Study. Anthem Press. p. 49. ISBN 9781783083497.
24. Arrian, "The Indica" Archived 25 May 2012 at the Wayback Machine
25. Kosmin 2014, p. 42.
26. Strabo Geographia Vol 3 Paragraph 36 Archived 16 November 2014 at the Wayback Machine
27. Aelian, Characteristics of animals, book XIII, Chapter 18, also quoted in The Cambridge History of India, Volume 1, p411
28. Asoka Mookerji Radhakumud. Motilal Banarsidass Publishing. 1995. p. 96. ISBN 9788120805828.
29. Bhalla, A. S. (2015). Monuments, Power and Poverty in India: From Ashoka to the Raj. I.B.Tauris. p. 18. ISBN 9781784530877.
30. "The Analysis of Indian Muria Empire affected from Achaemenid's architecture art". Journal of Subcontinent Researches. 6 (19): 149–174. 2014. Archived from the original on 2 April 2015.
31. Coningham, Robin; Young, Ruth (2015). The Archaeology of South Asia: From the Indus to Asoka, c.6500 BCE–200 CE. Cambridge University Press. p. 414. ISBN 9780521846974.
32. Waddell, L. A. (Laurence Austine) (1903). "Report on the excavations at Pātaliputra (Patna); the Palibothra of the Greeks". Calcutta, Bengal secretariat press.
33. Beal, Samuel (1884). Si-Yu-Ki: Buddhist Records of the Western World. London: Trubner & Co.
34. Beal, Samuel (1884). Si-Yu-Ki: Buddhist Records of the Western World. London.
35. Scott, David (May 1995). "Buddhism and Islam: Past to Present Encounters and Interfaith Lessons". Numen. 42 (2): 141–155. doi:10.1163/1568527952598657. JSTOR 32701721.
36. Delle cose maravigliose del mondo Tradotto da Giovan Vincenzo Belprato, Count of Antwerp, by Caius Julius Solinus (Solino), 1559, page 209.
37. Excavation sites in Bihar, Archaeological Survey of India, archived from the original on 28 October 2009, retrieved 13 September 2009.
38. Foreign Influence on Ancient India, de Krishna Chandra Sagar p.41

Sources

• Kosmin, Paul J. (2014), The Land of the Elephant Kings: Space, Territory, and Ideology in Seleucid Empire, Harvard University Press, ISBN 978-0-674-72882-0
• Sastri, Kallidaikurichi Aiyah Nilakanta, ed. (1988) [1967], Age of the Nandas and Mauryas (Second ed.), Delhi: Motilal Banarsidass, ISBN 978-81-208-0465-4

Further reading

• Bernstein, Richard (2001). Ultimate Journey: Retracing the Path of an Ancient Buddhist Monk (Xuanzang) who crossed Asia in Search of Enlightenment. Alfred A. Knopf, New York. ISBN 0-375-40009-5

[admin]

Indica (Megasthenes)
by Wikipedia
Accessed: 6/28/21

What Does Megasthenes Say About The Kings Who Ruled?

1. He calls Sandracottus the king of the Prassi and he mentions the names of Xandramus as predecessor and Sandrocyptus as successor to Sandracottus. There is absolutely no resemblance in these names to Bindusara (the successor to Chandragupta Maurya) and Mahapadma Nanda, the predecessor.

2. He makes absolutely no mention of Chanakya or Vishnugupta, the Acharya who helped Chandragupta ascend the throne.

3. He makes no mention of the widespread presence of the Baudhik or Sramana tradition [Rishi tradition] during the time of the Maurya empire.

4. He claims the capital is Palimbothra or Palibothra, and that the city exists near the confluence of the Ganga and the Eranaboas (Hiranyabahu). But the Puranas are clear that all the 8 dynasties after the Mahabharata war had their capital at Girivraja (Rajagriha), located in the foothills of the Himalayas. There is no mention of Pataliputra in the Puranas. So, the assumption made by Sir William that Palimbothra is Pataliputra has no basis in fact and is not attested by any piece of evidence. If the Greeks could pronounce the first P in (Patali) they could certainly have pronounced the second p in Putra, instead of bastardising it as Palimbothra. Granted the Greeks were incapable of pronouncing any Indian names, but there is no reason why they should not be consistent in their phonetics.

5. The empire of Chandragupta was known as Magadha Empire. It had a long history even at the time of Chandragupta Maurya. In Indian literature, this powerful empire is amply described by its name but the same is absent in Greek accounts. It is difficult to understand as to why Megasthenes did not use this name “Magadha” and instead used the word Prassi, which has no equivalent or counterpart in Indian accounts.

-- Historical Dates From Puranic Sources, by Prof. Narayan Rao

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle, M.A.

map of the known world, c. 194 BC

Indika (Greek: Ἰνδικά; Latin: Indica) is an account of Mauryan [No, "Sandrocottus"!!!] India by the Greek writer Megasthenes. The original work is now lost, but its fragments [not scraps of parchment; rather references] have survived in later Greek and Latin works. The earliest of these works are those by Diodorus Siculus, Strabo (Geographica), Pliny, and Arrian (Indica).[1][2]

Reconstruction

Megasthenes' Indica can be reconstructed using the portions preserved by later writers as direct quotations or paraphrase. The parts that belonged to the original text can be identified from the later works based on similar content, vocabulary and phrasing, even when the content has not been explicitly attributed to Megasthenes. Felix Jacoby's Fragmente der griechischen Historiker contains 36 pages of content traced to Megasthenes.[3]

E. A. Schwanbeck traced several fragments [not scraps of parchment; rather references] to Megasthenes, and based on his collection, John Watson McCrindle published a reconstructed version of Indica in 1887. However, this reconstruction is not universally accepted. Schwanbeck and McCrindle attributed several fragments [not scraps of parchment; rather references] in the writings of the 1st century BCE writer Diodorus to Megasthenes. However, Diodorus does not mention Megasthenes even once, unlike Strabo, who explicitly mentions Megasthenes as one of his sources. There are several differences between the accounts of Megasthenes and Diodorus: for example, Diodorus describes India as 28,000 stadia long from east to west; Megasthenes gives this number as 16,000. Diodorus states that Indus may be the world's largest river after Nile; Megasthenes (as quoted by Arrian) states that Ganges is much larger than Nile. Historian R. C. Majumdar points out that the Fragments I and II attributed to Megasthenes in McCrindle's edition cannot originate from the same source, because Fragment I describes Nile as larger than Indus, while Fragment II describes Indus as longer than Nile and Danube combined.[4]

Schwanbeck's Fragment XXVII includes four paragraphs from Strabo, and Schwanbeck attributes these entire paragraphs to Megasthenes. However, Strabo cites Megasthenes as his source only for three isolated statements in three different paragraphs. It is likely that Strabo sourced the rest of the text from sources other than Megasthenes: that's why he attributes only three statements specifically to Megasthenes.[4]

Another example is the earliest confirmed description of Gangaridai, which appears in the writings of Diodorus. McCrindle believed that Diodorus' source for this description was the now-lost book of Megasthenes. However, according to A. B. Bosworth (1996), Diodorus obtained this information from Hieronymus of Cardia: Diodorus described Ganges as 30 stadia wide; it is well-attested by other sources that Megasthenes described the median or minimum width of Ganges as 100 stadia.[5]

Fragments used by John Watson McCrindle to reconstruct Megasthenes' Indica

# / Work / Author-Editor / Section / Topic / Book number in Megasthenes' Indica

1 / Bibliotheca historica / Diodorus Siculus II.35-42 Summary of India Summary
2 / Bibliotheca historica / Diodorus Siculus III.63 Three persons named Dionusos Summary
3 / The Anabasis of Alexander / Arrian V. 6. 2-11 Boundaries and rivers / I
4 / Indica (Arrian) / Arrian II. 1. 7 Boundaries / I
5 / Geographica / Strabo XV.1.11 Boundaries and extent / I
6 / Geographica / Strabo II.1.7 Size of India / I
7 / Geographica / Strabo XV.1.12 Size of India / I
8 / Geographica / Strabo II.1.4 Size of India / I
9 / Indica (Arrian) / Arrian III. 7-8. Size of India / I
10 / Geographica / Strabo II.1.19 Ursa Major and shadows / I
11 / Natural History / Pliny VI. 22.6. Ursa Major / I
12 / Geographica / Strabo XV.1.20 Fertile soil / I
13 / Geographica / Strabo XV.1.37 Wild animals / I
14 / De Natura Animalium / Claudius Aelianus XVII 39. Indian apes / I
15 / De Natura Animalium / Claudius Aelianus XVI. 41 Winged scorpions and serpents / I
16 / Geographica / Strabo XV.1.56 Animals of India, and the Reed / I
17 / De Natura Animalium / Claudius Aelianus XVI. 20.21 Animals of India / I
18 / Natural History / Pliny VIII. 14. 1 Boa constrictor / I
19 / De Natura Animalium / Claudius Aelianus VIII.7 Of the Electric Eel. / I
20 / Natural History / Pliny VI.24.1 Taprobane / I
21 / Antigon. Caryst. / Antigonus of Carystus 647 Marine trees / I
22 / Indica (Arrian) / Arrian 4. 2-13. Indus and Ganges / I
23 / Natural History / Pliny VI. 21.9-22. 1. Indus and Ganges / I
24 / Polyhistor / Gaius Julius Solinus 52. 6-7. Indus and Ganges / I
25 / Indica (Arrian) / Arrian 6. 2-3. Silas river / I
26 / Anecdota Graeca / Jean François Boissonade de Fontarabie I. p. 419, Silas river / I
27 / Geographica / Strabo XV.1.38 Silas river / I
28 / Indica (Arrian) / Arrian 5. 2 Number of Indian rivers / I
29 / Geographica / Strabo XV.1.35-36 Pataliputra [No, Palibothra!!!] city / II
30 / Indica (Arrian) / Arrian 10 Pataliputra [No, Palibothra!!!] and Indian manners / II
31 / Geographica / Strabo XV.1.53-56 Indian manners / II
32 / Varia Historia / Claudius Aelianus iv.1. Indian manners / II
33 / Nicol. Damasc. / Nicolaus of Damascus 44 Indian manners / II
34 / Sermones / Stobaeus 42 Indian manners / II
35 / Deipnosophistae / Athenaeus iv. p. 153. Indian suppers / II
36 / Geographica / Strabo XV.1.57 Extraordinary tribes / II
37 / Natural History / Pliny VII. ii. 14-22 Extraordinary races / II
38 / Polyhistor / Gaius Julius Solinus 52. 26-30 Extraordinary races / II
39 / On the Face in the Moon (de facie in orbe lunae) in Moralia / Plutarch Opp. ed. Reisk, tom. ix. p. 701. Race of mouthless humans / II
40 / Indica (Arrian) / Arrian Xl.l.-XII.-9 7 castes of India / III
41 / Geographica / Strabo XV.1.39-41 7 castes of India / III
42 / Geographica / Strabo XV.1.50-52 Administration of public affairs; horses and elephants. / III
43 / De Natura Animalium / Claudius Aelianus XIII. 10. Horses and elephants / III
44 / Geographica / Strabo XV.1.41-43 Elephants / III
45 / Indica (Arrian) / Arrian ch. 13-14. Elephants / III
46 / De Natura Animalium / Claudius Aelianus XII. 44. Elephants / III
47 / De Natura Animalium / Claudius Aelianus XIII. 7. Of the diseases of Elephants. / III
48 / Geographica / Strabo XV.1.44 Gold-digging ants / III
49 / Indica (Arrian) / Arrian XV.5-7. Gold-digging ants / III
50 / Orations / Dio Chrysostom Or. 35 Gold-digging ants / III
51 / Geographica / Strabo XV.1.58-60 Indian philosophers / III
52 / Stromata / Clement of Alexandria I. p. 305 D Indian philosophers / III
53 / Praeparatio evangelica / Eusebius IX. 6 Indian philosophers / III
54 / Contra Julianum (Against Julian) / Cyril of Alexandria IV Indian philosophers / III
55 / Stromata / Clement of Alexandria I Indian philosophers / III
56 / Geographica / Strabo XV.1.68 Indian philosophers: Kalanos (Calanus) and Mandanis / III
57 / The Anabasis of Alexander / Arrian VII ii. 3-9 Indian philosophers: Kalanos (Calanus) and Mandanis / III
58 / Geographica / Strabo XV.1.68 Indians had not attacked anyone or faced external attacks; Dionysos and Herakles / IV
59 / Indica (Arrian) / Arrian V. 4-12. Indians had not attacked anyone or faced external attacks; Dionysos and Herakles / IV
60 / Contra Apion / Josephus I. 20 (T. II p. 451, Havere.) King of the Babylonians surpassed Herakles in greatness / IV
61 / Antiquitates Judaicae / Josephus X. ii. 1 (T. I p. 533, Havere.) King of the Babylonians surpassed Herakles in greatness / IV
62 / Zonar. Annal. Basileae 1557 / -- / -- / King of the Babylonians surpassed Herakles in greatness / IV
63 / G. Syncell. T. I. / George Syncellus??? p. 419, ed. Benn. (p. 221 ed. Paris, p. 177 ed. Venet.) King of the Babylonians surpassed Herakles in greatness / IV
64 / Fragments of Abydenus's writings in Praeparatio evangelica / Eusebius I. 41 (ed. Colon. 1688, p. 456 D) King of the Babylonians surpassed Herakles in greatness / IV
65 / Indica (Arrian) / Arrian 7-9. King of the Babylonians surpassed Herakles in greatness / IV
66 / Natural History / Pliny IX. 5 Pearls / IV
67 / Mirabilia / Phlegon of Tralles 33 Pandaian land / IV
68 / Natural History / Pliny VI. xxi. 4-5. Ancient history of Indians / IV
69 / Polyhistor / Gaius Julius Solinus 52. 5. Ancient history of Indians / IV
70 / The Anabasis of Alexander / Arrian VII. ii. 3-9. Indian philosophers: Kalanos (Calanus) and Mandanis / IV
71 / De Natura Animalium / Claudius Aelianus XII. 8. Elephants / (Doubtful fragments)
72 / De Natura Animalium / Claudius Aelianus III. 46. White elephant / (Doubtful fragments)
73 / De Recta in Deum Fide / Adamantius (Pseudo-Origen) vol. I. p. 904. Brachhmans (Brahmins) and their philosophy / (Doubtful fragments)
74 / Palladius De gentibus Indiae et Bragmanibus' / Palladius of Galatia pp. 8, 20 et seq. ed. Londin. 1668. Indian philosophers: Kalanos (Calanus) and Mandanis / (Doubtful fragments)
75 / De Moribus Brachmanorum / Ambrose pp. 62, 68 et seq. ed. Pallad. Londin. 1668. Calanus and Mandanis / (Doubtful fragments)
76 / Natural History / Pliny VI. 21. 8-23. 11. Indian races / (Doubtful fragments)
77 / Polyhistor / Gaius Julius Solinus 52. 6-17. Catalogue of Indian Races. / (Doubtful fragments)
78 / Stratagems / Polyaenus I. 1. 1-3. Dionysos / (Doubtful fragments)
79 / Stratagems / Polyaenus I. 3. 4. Hercules and Pandaea / (Doubtful fragments)
80 / De Natura Animalium / Claudius Aelianus XVI. 2-22. Beasts of India / (Doubtful fragments)

India according to the reconstructed text

According to the text reconstructed by J. W. McCrindle, Megasthenes' Indica describes India as follows:

Geography

India is a quadrilateral-shaped country, bounded by the ocean on the southern and the eastern side.[6] The Indus river forms the western and the north-western boundary of the country, as far as the ocean.[7] India's northern border reaches the extremities of Tauros. From Ariana to the Eastern Sea, it is bound by mountains that are called Kaukasos by the Macedonians. The various native names for these mountains include Parapamisos, Hemodos and Himaos (the Himalayas).[8] Beyond Hemodos, lies Scythia inhabited by the Scythians known as Sakai.[9] Besides Scythia, the countries of Bactria and Ariana border India.[10]

At the extreme point of India, the gnomon of the sundial often casts no shadow, and the Ursa Major is invisible at night. In the remotest parts, the shadows fall southward, and even Arcturus is not visible.[9]

India has many large and navigable rivers, which arise in the mountains on its northern border. Many of these rivers merge into Ganges, which is 30 stadia wide at its source, and runs from north to south. The Ganges empties into the ocean that forms the eastern boundary of Gangaridai.[11] Other nations feared Gangaridai's huge force of the biggest elephants, and therefore, Gangaridai had never been conquered by any foreign king.[12]

Indus also runs from north to south, and has several navigable tributaries. The most notable tributaries are Hupanis, the Hudaspes, and the Akesines.[13] One peculiar river is Sillas, which originates from a fountain of the same name. Everything cast into this river sinks down to the bottom - nothing floats in it.[10] In addition, there are a large number of other rivers, supplying abundant water for agriculture. According to the native philosophers and natural scientists, the reason for this is that the bordering countries are more elevated than India, so their waters run down to India, resulting in such a large number of rivers.[14]

History


Mauryan[???] remains of a wooden palissade at Bulandi Bagh site of Pataliputra.


Mauryan[???] remains of a wooden palissade at Bulandi Bagh site of Pataliputra.

In the primitive times, the Indians lived on fruits and wore clothes made of animal skin, just like the Greeks. The most learned Indian scholars say that Dionysus invaded India, and conquered it. When his army was unable to bear the excessive heat, he led his soldiers to the mountains called Meros for recovery; this led to the Greek legend about Dionysus being bred in his father's thigh (meros in Greek).[a] Dionysus taught Indians several things including how to grow plants, make wine and worship. He founded several large cities, introduced laws and established courts. For this reason, he was regarded as a deity by the Indians. He ruled entire India for 52 years, before dying of old age. His descendants ruled India for several generations, before being dethroned and replaced by democratic city-states.[16]

The Indians who inhabit the hill country also claim that Herakles was one of them. Like the Greeks, they characterize him with the club and the lion's skin. According to them, Herakles was a powerful man who subjugated evil beasts. He had several sons and one daughter, who became rulers in different parts of his dominion. He founded several cities, the greatest of which was Palibothra (Pataliputra[???]). Herakles built several places in this city, fortified it with water-filled trenches and settled a number of people in the city. His descendants ruled India for several generations, but never launched an expedition beyond India. After several years, the royal rule was replaced by democratic city states, although there existed a few kings when Alexander invaded India.[17]

33 Such, then, are the traditions regarding Dionusos and his descendants current among the Indians who inhabit the hill-country. 34 They further assert that Herakles [Apparently Siva is meant, though his many wives and sons are unknown to Hindu mythology.— ED.] also was born among them. 34 They assign to him, like the Greeks, the club and the lion's skin. He far surpassed other men in personal strength, and prowess, and cleared sea and land of evil beasts. 35 Marrying many wives he begot many sons, but one daughter only. The sons having reached man's estate, he divided all India into equal portions for his children, whom he made kings in different parts of his dominions. He provided similarly for his only daughter, whom he reared up and made a queen. 36 He was the founder, also, of no small number of cities, the most renowned and greatest of which he called Palibothra. He built therein many sumptuous palaces, and settled within its walls a numerous population. The city he fortified with trenches of notable dimensions, which were filled with water introduced from the river. 37 Herakles, accordingly, after his removal from among men, obtained immortal honour; and his descendants, having reigned for many generations and signalized themselves by great achievements, neither made any expedition beyond the confines of India, nor sent out any colony abroad. 38 At last, however, after many years had gone, most of the cities adopted the democratic form of government, though some retained the kingly until the invasion of the country by Alexander. 39

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle

The jurisprudence of the Hindus and Arabs being the field which I have chosen for my peculiar toil, you cannot expect that I should greatly enlarge your collection of historical knowledge; but I may be able to offer you some occasional tribute; and I cannot help mentioning a discovery which accident threw in my way, though my proofs must be reserved for an essay which I have destined for the fourth volume of your Transactions. To fix the situation of that Palybothra (for there may have been several of the name) which was visited and described by Megasthenes, had always appeared a very difficult problem, for though it could not have been Prayaga, where no ancient metropolis ever stood, nor Canyacubja, which has no epithet at all resembling the word used by the Greeks; nor Gaur, otherwise called Lacshmanavati, which all know to be a town comparatively modern, yet we could not confidently decide that it was Pataliputra, though names and most circumstances nearly correspond, because that renowned capital extended from the confluence of the Sone and the Ganges to the site of Patna, while Palibothra stood at the junction of the Ganges and Erannoboas, which the accurate M. D'Ancille had pronounced to be the Yamuna; but this only difficulty was removed, when I found in a classical Sanscrit book, near 2000 years old, that Hiranyabahu, or golden armed, which the Greeks changed into Erannoboas, or the river with a lovely murmur, was in fact another name for the Sona itself; though Megasthenes, from ignorance or inattention, has named them separately. This discovery led to another of greater moment, for Chandragupta, who, from a military adventurer, became like Sandracottus the sovereign of Upper Hindustan, actually fixed the seat of his empire at Pataliputra, where he received ambassadors from foreign princes; and was no other than that very Sandracottus who concluded a treaty with Seleucus Nicator; so that we have solved another problem, to which we before alluded, and may in round numbers consider the twelve and three hundredth years before Christ, as two certain epochs between Rama, who conquered Silan a few centuries after the flood, and Vicramaditya, who died at Ujjayini fifty-seven years before the beginning of our era.

-- Discourse X. Delivered February 28, 1793, P. 192, Excerpt from "Discourses Delivered Before the Asiatic Society: And Miscellaneous Papers, on The Religion, Poetry, Literature, Etc. of the Nations of India", by Sir William Jones

Flora and fauna

India has several mountains with fruit trees of every kind.[9] There are a large number of animal species in India. The Indian elephants are far stronger than the Libyan elephants, because of the abundance of food on the Indian soil. The elephants are domesticated in large numbers, and trained for war.[18] The gestation period of the elephants ranges from 16 to 18 months, and the oldest of the elephants live up to 200 years.[19]

Economy

Gold, silver, copper and iron are abundant on Indian soil. Tin and other metals are used for making a number of tools, weapons, ornaments, and other articles.[18]

India has very fertile plains, and irrigation is practised widely.[18] The main crops include rice, millet, a crop called bosporum, other cereals, pulses and other food plants.[20] There are two crop cycles per year, since rain falls in both summer and winter. At the time of summer solstice, rice, millet, bosporum and sesamum are sown. During winter, wheat is sown.[20]

No famines have ever occurred in India because of the following reasons:[21]

• The Indians are always assured of at least one of the two seasonal crops
• There are a number of spontaneously growing fruits and edible roots available.
• The Indian warriors regard those engaged in agriculture and animal husbandry as sacred. Unlike the warriors in other countries, they do not ravage farms during war conquests. Moreover, the warring sides never destroy the enemy land with fire or cut down its trees.

Food and Clothing

Indian beverage is a liquor composed from rice instead of barley, when the Indians are at supper a table is placed before each person, this being like a tripod. There is placed upon it a golden bowl, into which they first put rice, boiled as one would boil barley, and then they add many dainties prepared according to Indian receipts. [22]

In contrast to the general simplicity of their style, they love finery and ornament. Their robes are worked in gold, and ornamented with precious stones, and they wear also flowered garments made of the finest muslin. Some have attendants walking behind hold up umbrellas over them: for they have a high regard for beauty, and avail themselves of every device to improve their looks.[23]

Society

Because of its large size, India is inhabited by many diverse races, all of which are indigenous. India has no foreign colony, and Indians have not established any colonies outside India.[10] The Indians are of above average stature, because of abundant food, fine water and pure air. They are well-skilled in art.[18]

A law, prescribed by ancient Indian philosophers, bans slavery. The law treats everyone equally, but allows the property to be unevenly distributed.[24]

The population of India is divided into 7 endogamous and hereditary castes:[25]

1. Philosophers
o Not numerous compared to other castes, but most prominent
o Exempted from all public duties
o Neither masters, nor servants
o "believed to be most dear to the gods, and to be the most conversant with matters pertaining to Hades"
o Engaged by others to offer sacrifices and perform funerary rites, for which they received valuable gifts and privileges
o At the beginning of the year, they make prophecies about droughts, rain storms, propitious winds, diseases and other topics. Based on these prophecies, the citizens and the rulers make adequate preparations. A philosopher whose prophecy fails receives strong criticism and has to observe silence for the rest of his life, but otherwise incurs no penalty.
2. Farmers
o Most numerous of all castes
o Live in villages, and avoid visiting towns
o Exempted from fighting and other public duties
o Regarded as public benefactors, and protected from damage during wars, even by enemy warriors
o Pay a land tribute to the ruler, the official land owner
o In addition, they remit 1/4th of their produce to the state treasury
3. Herders
o Live in tents, outside villages and towns
o Hunt and trap crop-destroying birds and animals
4. Artisans
o Create weapons as well as tools for farmers and others
o Exempted from paying taxes, and receive a maintenance from the state exchequer
5. Military
o Second most numerous among the castes
o Well-organized and equipped for war
o Indulge in amusements and idleness during peaceful times
o Maintained at state expense, along with war horses and elephants
6. Overseers
o Carry out administrative tasks
o Report to the king or (in states not ruled by kings) magistrates
7. Councillors and Assessors
o Composed of wise people with good character
o Deliberate on public affairs; included the royal advisers, state treasurers, dispute arbitrators; the army generals and chief magistrates also usually belonged to this class.
o Least numerous, but most respected

Philosophy

Megasthenes makes a different division of the philosophers, saying that they are of two kinds - one of which he calls the Brachmanes, and the other the Sarmanes. Of the Sarmanes he tells us that those who are held in most honour are called the Hylobioi. Next in honour to the Hylobioi are the physicians, since they are engaged in the study of the nature of man. Besides these there are diviners and sorcerers. Women pursue philosophy with some of them. [26]

Megasthenes also comments on the presence of pre-Socratic views among the Brahmans in India and Jews in Syria. Five centuries later Clement of Alexandria, in his Stromateis, may have misunderstood Megasthenes to be responding to claims of Greek primacy by admitting Greek views of physics were preceded by those of Jews and Indians. Megasthenes, like Numenius of Apamea, was simply comparing the ideas of the different ancient cultures.[27]

Administration

The foreigners are treated well. Special officers are appointed to ensure that no foreigner is harmed, and judges hand out harsh punishment to those who take unfair advantage of the foreigners. Sick foreigners are attended by physicians and taken care of. Foreigners who die in India are buried, and their property is delivered to their relatives.[28]

Historical reliability

Later writers such as Arrian, Strabo, Diodorus, and Pliny refer to Indika in their works. Of these writers, Arrian speaks most highly of Megasthenes, while Strabo and Pliny treat him with less respect.

The first century Greek writer Strabo called both Megasthenes and his succeeding ambassador Deimachus liars, and stated that "no faith whatever" could be placed in their writings.[29] The Indika contained numerous fantastical stories, such as those about tribes of people with no mouths, unicorns and other mythical animals, and gold-digging ants.[30] Strabo directly contradicted these descriptions, assuring his readers that Megasthenes' stories, along with his recounting of India’s founding by Hercules and Dionysus, were mythical with little to no basis in reality.[31] Despite such shortcomings, some authors believe that Indika is creditworthy, and is an important source of information about the contemporary Indian society, administration and other topics.[30]

According to Paul J. Kosmin, Indica served a legitimizing purpose for Seleucus I and his actions in India.[32] It depicts contemporary India as an unconquerable territory, arguing that Dionysus was able to conquer India, because before his invasion, India was a primitive rural society. Dionysus' urbanization of India makes India a powerful, impregnable nation. The later ruler — the Indian Herakles — is presented as a native of India, despite similarities with the Greek Heracles. This, according to Kosmin, is because now India is shown as unconquerable.[33] Megasthenes emphasizes that no foreign army had been able to conquer India (since Dionysus) and Indians had not invaded a foreign country either. This representation of India as an isolated, invincible country is an attempt to vindicate Seleucus' peace treaty with the Indian emperor [34] through which he abandoned territories he could never securely hold, stabilized the East, and obtained elephants with which he could turn his attention against his great western rival, Antigonus Monophthalmus. [35]

Megasthenes states that there were no slaves in India, but the Arthashastra attests to the existence of slavery in contemporary India;[36] Strabo also counters Megasthenes's claim based on a report from Onesicritus. Historian Shireen Moosvi theorizes that slaves were outcastes, and were not considered members of the society at all.[37] According to historian Romila Thapar, the lack of sharp distinction between slaves and others in the Indian society (unlike the Greek society) may have confused Megasthenes: Indians did not use large-scale slavery as a means of production, and slaves in India could buy back their freedom or be released by their master.[38]

Megasthenes mentions seven castes in India, while the Indian texts mention only four social classes (varnas). According to Thapar, Megasthenes' categorization appears to be based on economic divisions rather than the social divisions; this is understandable because the varnas originated as economic divisions. Thapar also speculates that he wrote his account some years after his visit to India, and at this time, he "arrived at the number seven, forgetting the facts as given to him". Alternatively, it is possible that the later authors misquoted him, trying to find similarities with the Egyptian society, which according to Herodotus, was divided into seven social classes.[39]

Megasthenes claims that before Alexander, no foreign power had invaded or conquered Indians, with the exception of the mythical heroes Hercules and Dionysus. However, it is known from earlier sources - such as the inscriptions of Darius the Great and Herodotus - that the Achaemenid Empire included parts of north-western part of India (present-day Pakistan). It is possible that the Achaemenid control did not extend much beyond the Indus River, which Megasthenes considered to be the border of India. Another possibility is that Megasthenes intended to understate the power of the Achaemenid Empire, a rival of the Greeks.[40]

Notes

1. D. R. Patil suggests that the Rigvedic Prithu was a vegetarian deity, associated with Greek god Dionysus.[15]

References

1. Upinder Singh (2008). A History of Ancient and Early Medieval India. Pearson Education India. p. 324. ISBN 9788131711200.
2. Christopher I. Beckwith (2015). Greek Buddha: Pyrrho's Encounter with Early Buddhism in Central Asia. Princeton University Press. p. 62. ISBN 9781400866328.
3. Paul J. Kosmin 2013, p. 99.
4. Sandhya Jain 2011, p. 22.
5. A. B. Bosworth 1996, pp. 188-189.
6. J. W. McCrindle 1877, p. 49.
7. J. W. McCrindle 1877, p. 46.
8. J. W. McCrindle 1877, pp. 48-49.
9. J. W. McCrindle 1877, p. 30.
10. J. W. McCrindle 1877, p. 35.
11. J. W. McCrindle 1877, p. 33.
12. J. W. McCrindle 1877, p. 33-34.
13. J. W. McCrindle 1877, p. 34.
14. J. W. McCrindle 1877, p. 34-35.
15. Nagendra Kumar Singh (1997). Encyclopaedia of Hinduism. Anmol Publications. pp=1714. ISBN 978-81-7488-168-7.
16. J. W. McCrindle 1877, p. 35-38.
17. J. W. McCrindle 1877, p. 39-40.
18. J. W. McCrindle 1877, p. 31.
19. J. W. McCrindle 1877, p. 44.
20. J. W. McCrindle 1877, p. 32.
21. J. W. McCrindle 1877, p. 32-33.
22. Gochberg, Donald S., et al., ed. "World Literature and Thought: Volume I: The Ancient Worlds"; Fort Worth, TX; Harcourt Brace; 1997, pp. 410-416.
23. Gochberg, Donald S., et al., ed. "World Literature and Thought: Volume I: The Ancient Worlds"; Fort Worth, TX; Harcourt Brace; 1997, pp. 410-416.
24. J. W. McCrindle 1877, p. 40.
25. J. W. McCrindle 1877, p. 40-44.
26. FRAGM. XLI Strab. XV. 1. 58-60,--pp. 711-714 Of the Indian Philosophers. J. W. McCrindle.
27. Bezalel Bar-Kochva 2010, p. 157: "He does not respond to the implied claim of Greek primacy, presumably because he did not have, and could not have had, hard information about the beginnings of "parallel" opinions among the Brahmans."
28. J. W. McCrindle 1877, p. 44-45.
29. Allan Dahlaquist 1996, p. 28.
30. Irfan Habib; Vivekanand Jha (2004). Mauryan India. A People's History of India. Aligarh Historians Society / Tulika Books. p. 19. ISBN 978-81-85229-92-8.
31. Strabo, Geography, Book XV, Chapter 1
32. Paul J. Kosmin 2013, p. 91.
33. Paul J. Kosmin 2013, p. 98-100.
34. Paul J. Kosmin 2013, p. 103-104.
35. Paul J. Kosmin 2013, p. 98.
36. Romila Thapar 1990, p. 89.
37. Shireen Moosvi 2004, p. 548.
38. Romila Thapar 1990, pp. 89-90.
39. Romila Thapar 2012, p. 118.
40. H. C. Raychaudhuri 1988, pp. 31-32.

Bibliography

• A. B. Bosworth (1996). Alexander and the East. Clarendon. p. 192. ISBN 978-0-19-158945-4.
• Allan Dahlaquist (1996). Megasthenes and Indian Religion- Volume 11 of History and Culture Series. Motilal Banarsidass Publ. p. 386. ISBN 81-208-1323-5.
• H. C. Raychaudhuri (1988) [1967]. "India in the Age of the Nandas". In K. A. Nilakanta Sastri (ed.). Age of the Nandas and Mauryas (Second ed.). Delhi: Motilal Banarsidass. ISBN 978-81-208-0466-1.
• J. W. McCrindle (1877). Ancient India As Described By Megasthenes And Arrian. London: Trübner & Co.
• Megasthenes (1846), E. A. Schwanbeck (ed.), Indica, Sumptibus Pleimesii, bibliopolae (Original Oxford University)
• Paul J. Kosmin (2013). "Apologetic Ethnography: Megasthenes' Indica and the Seleucid Elephant". In Eran Almagor, Joseph Skinner (ed.). Ancient Ethnography: New Approaches. Bloomsbury Publishing. ISBN 9781472537607.
• Radha Kumud Mookerji (1988) [first published in 1966], Chandragupta Maurya and his times (4th ed.), Motilal Banarsidass, ISBN 81-208-0433-3
• Romila Thapar (2012). Aśoka and the Decline of the Mauryas. Oxford University Press India. ISBN 978-0-19-908868-3.
• Romila Thapar (1990). A History of India. Penguin Books Limited. ISBN 978-0-14-194976-5.
• Sandhya Jain (2011). The India They Saw (Vol-1). Ocean Books. ISBN 978-81-8430-106-9.
• Shireen Moosvi (2004). "Domestic service in precolonial India: Bondage, caste and market". In Antoinette Fauve-Chamoux (ed.). Domestic Service and the Formation of European Identity. Peter Lang. ISBN 978-3-03910-589-2.

[admin]

The Indika of Megasthenes
by R.C. Majumdar
University of Pennsylvania
Journal of the American Oriental Society
Vol. 78, No. 4, pp. 273-276 (4 pages)
Published by: American Oriental Society
(Oct. - Dec., 1958)

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle

Highlights:

Arrian [86/89-146/160 A.D.] mentions Nearchus, Eratosthenes [276 BC–195/194 BC)], Megasthenes and other writers as his sources of information. In one place he refers to Eratosthenes as "the safest authority" (para III). He specifically mentions Megasthenes many times, but evidently sets little value on his account, for he says: "Beyond that limit (the Hyphasis [Beas]) we have no real knowledge of the country since this is the sort of account which Megasthenes gives us of an Indian river." He then refers to the river Silas, on whose water, according to Megasthenes, nothing floats but sinks to the bottom…

Again, referring to the statement of Megasthenes 'that the Indian tribes number in all 118,' Arrian makes the very apposite comment: "I am at a loss to conjecture how he arrived at it, for the greater part of India he did not visit, nor is mutual intercourse maintained between all the tribes." Again Arrian says: "Megasthenes avers that the tradition about (gold-digging) ants is strictly true," and very correctly observed: "Megasthenes writes what he had heard from hearsay.…

The passages which we may justly regard as either quoted from the Indika of Megasthenes, or derived from it through secondary sources, are comparatively few in number. Leaving aside the incredible stories of fabulous races and wild animals, etc., the passages of real interest to Indian history that may be confidently referred to the authority of Megasthenes may be listed as follows:

1. The geography of India (Fragments II to VIII). The account is chiefly based on Eratosthenes, and Megasthenes agrees with him (p. 50) or with Deimachos (p. 51).
2. That in the southern parts of India the constellation of the Bear disappears from view and shadows fall in opposite direction (Fragments IX-X).
3. The soil of India produces two crops every year, both of fruits and grain (Fragment XI)…
4. A short account of Taprobane [Sri Lanka] (Fragment XVIII, p. 62).
5. The mean breadth of the Ganges is 100 stadia and its least depth 20 fathoms (Fragment XXV). The rest of the Fragment XXV, containing the description of Pataliputra, may be ascribed to Megasthenes, for it is repeated with fuller details by Arrian (Para X) who definitely mentions Megasthenes as his authority.
6. The passages quoted by Arrian about Palimbothra and absence of slavery in India (Fragment XXVI, p. 68, last 9 lines, and line 1 of p. 69)…
7. One sentence at the beginning and another at the end [of the long Fragment XXVII]…
8. Description of Indian supper (Fragment XXVIII, p. 74).
9. Seven castes among the Indians (Fragments XXXII, XXXIII, p. 83).
10. Description of Indian philosophers (Fragment XLI, p. 97; XLII, pp. 103-4)…
11. [A] few references [in Fragment XLVI (p. 107)]…
12. The assertion that the women of the Pandaian realm bear children when they are six years of age (Fragment LI, p. 14).
13-14. Two passages in Arrian's Indika; one giving a fuller account of the rivers of India (Paras IV, V); the other enumerating the Indian tribes and giving the legendary account of the parts played by Dionysos and Herakles in India (Paras VII-IX).

-- The Indika of Megasthenes, by R.C. Majumdar

Since the beginning of Indological studies the Indika of Megasthenes has deservedly occupied a very high place among the classical sources of ancient Indian history. The book itself has never come to light, and the German scholar Dr. Schwanbeck rendered a great service by bringing together all the passages of the lost treatise which have survived in quotations by later classical writers. The English translation of Dr. Schwanbeck's collected fragments of Indika by J.W. McCrindle has made this book familiar to all students of ancient Indian history. For nearly a century they have made full use of this first-hand account of India written by an eye-witness at the beginning of the Maurya period, i.e., towards the end of the fourth century B.C.

When the study of Indology was at its infancy, one could not be expected to be very critical of the few sources of first-rate importance then available to him. Schwanbeck's reconstruction of Megasthenes' Indika was therefore accepted without criticism, and this mental attitude, by sheer inertia, has persisted among the students of ancient Indian history even today.1 [B.C.J. Timmer has discussed this question in her doctoral dissertation entitled "Megasthenes en de Indische Mastachappij" (Amsterdam, 1930). She has not, however, gone very deeply into this subject.]

But the progress of Indological studies has rendered it necessary to subject many of the old accepted notions to a searching criticism, and among these should be included the genuineness of the Indika of Megasthenes, as reconstructed by Schwanbeck, and rendered familiar by McCrindle's translation into English.

The passages which Dr. Schwanbeck has accepted as "fragments" of the Indika may be divided into four classes:

1. The passages in the works of later writers which are explicitly attributed to Megasthenes.

2. Passages closely resembling those under (1), though not specifically attributed to Megasthenes.

3. Passages preceding or following those under (1) or (2).

4. Long passages including, incidentally, those under (2) or (3).

A typical instance of the fourth category is furnished by the very first Fragment, from the History of Diodorus (II. 35-42), which Schwanbeck has labelled as "An Epitome of Megasthenes." Now, it is a notable fact that in this long extract, extending over 14 printed pages, the name of Megasthenes is conspicuous by its absence. The account of Diodorus seems more likely to be a compilation from many sources; at least there is no ground to suppose that he depended solely, or even mainly, upon Megasthenes, far less, intended to give a summary of his work. If such had been the case we could certainly expect a reference to the name or authority of Megasthenes. The English translator of the work of Diodorus was constrained to observe: "It cannot be known whether Diodorus used Megasthenes directly or through a medium; his failure to mention his name a single time is a little surprising, if he used him directly."2 ["Diodorus of Sicily" -- English translation by C.H. Oldfather (1935). See Introduction.]

The theory that Diodorus used Megasthenes through a medium may explain the omission of Megasthenes' name, but certainly reduces, to a very considerable extent, the value of the account as a genuine source of information based on the Indika of Megasthenes alone.

But even if we assume that Diodorus derived his knowledge of the Indika from other books, there are good grounds to believe that he had relied on sources other than the Indika. The statement that Alexander advanced as far as the Ganges3 [Diodorus, para. 37.] may be cited as an instance. It seems almost incredible that such a statement could be made by Megasthenes, belonging to the same generation as Alexander and living in Pataliputra on the banks of the Ganges in intimate touch with the king and the people who must have possessed a correct knowledge of the extent of Alexander's advance in India.

If, therefore, it is practically certain that Diodorus utilised sources other than the Indika of Megasthenes, it is obviously impossible to regard his long account of India as "an epitome of Megasthenes." Further, one might naturally doubt whether any passage in the account of Diodorus, save and except those included under category (2) mentioned above, may be regarded as based, even indirectly, on the authority of Megasthenes.

We may now consider the passages belonging to category (3). A typical instance is furnished by the long extract from Strabo's Geography (XV. 1. 53-56), included under Fragment XXVII (p. 69).4 [The pages refer to McCrindle's Translation (London, 1877).] Now, here Megasthenes is definitely cited as authority for the statement that "those who were in the camp of Sandrakottos, wherein lay 40,000 men, found that the thefts reported on any one day did not exceed the value of 200 drachmae."5 [McCrindle gives the number of men in the camp as 400,000 (p. 69). But H.L. Jones, in his translation of Strabo's Geography, gives the number as 40,000 which is evidently the correct figure.]

'He (Seleukos) crossed the Indus and waged war on Sandrokottos, king of the Indians who dwelt about it, until he made friends and entered into relations of marriage with him.' So also Strabo (xv. p. 724): — 'Seleukos Nikator gave to Sandrokottos' (sc. a large part of Ariane). Conf. p. 689: — 'The Indians afterwards held a large part of Ariane, (which they had received from the Makedonians), 'entering into marriage relations with him, and receiving in return five hundred elephants' (of which Sandrakottos had nine thousand— Plinius, vi. 22-5); and Plutarch, Alex. 62:— 'For not long after, Androkottos, being king, presented Seleukos with five hundred elephants, and with six hundred thousand [600,000] men attacked and subdued all India.' Phylarchos (Fragm. 28) in Athenaeus, p. 18 D., refers to some other wonderful enough presents as being sent to Seleukos by Sandrokottos.

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle

But there is no such specific reference to Megasthenes in the case of the other statements that follow. There is no obvious reason to take the long extract of more than four pages as a running quotation from the Indika of Megasthenes, particularly as the passage from the Indika is specifically quoted only in support of a general statement quoted by Strabo that theft is of very rare occurrence. Besides, the subject matters dealt with in the passages that follow are quite different. It is well known that Strabo utilised many other sources and has specifically referred to some of them. There is thus no reason to suppose that Strabo must necessarily have derived from Megasthenes all the information included in a single para or consecutive paras, which contain any reference to Megasthenes. There is, no doubt, a possibility, that some of the passages, if not all, in these paras, were based on the Indika of Megasthenes. But it is surely unsafe to proceed on this assumption; and then it is difficult to find out which of the passages falls in this category. It is to be noted that at the end of the very same Fragment (XXVII), another specific reference is made to Megasthenes. This indirectly supports the view that the passages in Fragment XXVII, in between the two specific quotations from the Indika, are not based on that authority. For in that case a second reference to Megasthenes was uncalled for.

Many Indologists, consciously or unconsciously, make the tacit assumption that the Indika of Megasthenes gave the most elaborate and reliable account of India, and the subsequent classical writers drew so largely upon it that one may be excused in regarding their account as based on Megasthenes unless otherwise mentioned. This assumption is belied by the fact that the classical writers themselves had no great faith in the veracity of Megasthenes and did not put a very high value on his Indika. How far this view was just or not, it is immaterial for our present purpose to decide. But the existence of such a general belief should make us hesitate to refer all that they said, without any specific mention of the source, to the authority of Megasthenes.

Strabo (p. 70) says, 'Generally speaking, the men who have hitherto written on the affairs of India were a set of liars, — Deimachos holds the first place in the list, Megasthenes comes next; while Onesikritos and Nearchos, with others of the same class, manage to stammer out a few words (of truth). Of this we became the more convinced whilst writing the history of Alexander. No faith whatever can be placed in Deimachos and Megasthenes. They coined the fables concerning men with ears large enough to sleep in, men without any mouths, without noses, with only one eye, with spider legs, and with fingers bent backward. They renewed Homer's fables concerning the battles of the cranes and pygmies, and asserted the latter to be three spans high. They told of ants digging for gold, and Pans with wedge-shaped heads, of serpents swallowing down oxen and stags, horns and all, — meantime, as Eratosthenes has observed, accusing each other of falsehood. Both of these men were sent as ambassadors to Palimbothra, — Megasthenes to Sandrokottos, Deimachos to Amitrochados his son, — and such are the notes of their residence abroad, which I know not why, they thought fit to leave.'

-- Ancient India as Described by Megasthenes and Arrian; Being a Translation of the Fragments of the Indika of Megasthenes Collected by Dr. Schwanbeck, and of the First Part of the Indika of Arrian, by J.W. McCrindle

Aristobulus [375 B.C.-301 B.C.], whose treatise on India is also lost, was another author of repute, holding more or less the same status as Megasthenes. Arrian [86/89-146/160 A.D.] mentions Nearchus, Eratosthenes, Megasthenes and other writers as his sources of information. In one place he refers to Eratosthenes as "the safest authority" (para III). He specifically mentions Megasthenes many times, but evidently sets little value on his account, for he says: "Beyond that limit (the Hyphasis [Beas]) we have no real knowledge of the country since this is the sort of account which Megasthenes gives us of an Indian river." He then refers to the river Silas, on whose water, according to Megasthenes, nothing floats but sinks to the bottom.6 [McCrindle's translation, Para VI, p. 196).]

The Beas River (Sanskrit: Vipāśā; Hyphasis in Ancient Greek) is a river in north India. The river rises in the Himalayas in central Himachal Pradesh, India, and flows for some 470 kilometres (290 mi) to the Sutlej River in the Indian state of Punjab. Its total length is 470 kilometres (290 mi) and its drainage basin is 20,303 square kilometres (7,839 sq mi) large.

Beas River [Hyphasis], by Wikipedia

It might be argued that as Megathenes lived at Pataliputra, the accounts of the eastern parts of Northern India, as given by the classical writers, were most probably based on his Indika. But Arrian quite clearly tells us that "A FEW AUTHORS have described the country as far as the river Ganges and the parts near its mouth and the city of Palimbothra."7 [Ibid., Para II, p. 184).] Thus there were other sources of information about Palimbothra (Pataliputra) and the neighbouring region than the Indika of Megasthenes.

The above discussion would make it clear that the passages which we may justly regard as either quoted from the Indika of Megasthenes, or derived from it through secondary sources, are comparatively few in number. Leaving aside the incredible stories of fabulous races and wild animals, etc., the passages of real interest to Indian history that may be confidently referred to the authority of Megasthenes may be listed as follows:

1. The geography of India (Fragments II to VIII). The account is chiefly based on Eratosthenes, and Megasthenes agrees with him (p. 50) or with Deimachos (p. 51).

2. That in the southern parts of India the constellation of the Bear disappears from view and shadows fall in opposite direction (Fragments IX-X).

3. The soil of India produces two crops every year, both of fruits and grain (Fragment XI). The rest of Fragment XI (pp. 54-5) does not belong to the Indika as it is specifically referred to Eratosthenes.

4. A short account of Taprobane [Sri Lanka] (Fragment XVIII, p. 62).

5. The mean breadth of the Ganges is 100 stadia and its least depth 20 fathoms (Fragment XXV). The rest of the Fragment XXV, containing the description of Pataliputra, may be ascribed to Megasthenes, for it is repeated with fuller details by Arrian (Para X) who definitely mentions Megasthenes as his authority.

6. The passages quoted by Arrian about Palimbothra and absence of slavery in India (Fragment XXVI, p. 68, last 9 lines, and line 1 of p. 69). The rest of Fragment XXVI cannot, however, be definitely attributed to Megasthenes, though it seems to be very likely.

7. The attribution of the long Fragment XXVII, excepting one sentence at the beginning and another at the end, to Megasthenes is very doubtful as already pointed out above.

8. Description of Indian supper (Fragment XXVIII, p. 74).

9. Seven castes among the Indians (Fragments XXXII, XXXIII, p. 83).

10. Description of Indian philosophers (Fragment XLI, p. 97; XLII, pp. 103-4).

11. Fragment XLVI (p. 107) contains a few references to Megasthenes but the whole passage is obviously based upon a number of different accounts.

12. The assertion that the women of the Pandaian realm bear children when they are six years of age (Fragment LI, p. 14).

13-14. Two passages in Arrian's Indika; one giving a fuller account of the rivers of India (Paras IV, V); the other enumerating the Indian tribes and giving the legendary account of the parts played by Dionysos and Herakles in India (Paras VII-IX).

As regards other passages included in Schwanbeck's (and McCrindle's) Indika of Megasthenes, their authenticity is highly doubtful and it may be justly questioned whether one should regard them as emanating from Megasthenes. Among these the most important are:

1. Fragment I (the so-called "Epitome of Megasthenes" by Diodorus) except the topics or passages included in the above list.

2. The major part of Fragment XXVII describing the manners and customs of the Indians.

3. Fragment XXXIV describing the Municipal and Military Boards of Administration.

Very important conclusions have been drawn from these fragments regarding the state of things in the time of Chandragupta Maurya, and they have figured prominently in the discussion of the genuineness of the text of Arthasastra, attributed to Kautilya. In particular, the absence of any reference to the Municipal and Military Boards in Kautilya's Arthasastra has been put forward as a strong argument against accepting that work as belonging to the time of Chandragupta Maurya. In view of such great importance naturally attaching to any statement of Megasthenes, we must be very cautious in attributing to Megasthenes any passage for which his name or authority is not specifically cited.

In conclusion, a few words may be said about the veracity of Megasthenes. Schwanbeck has discussed this question at length and discredited the views of ancient writers who included Megasthenes among "those writers who are given to lying and least worthy of credit," and ranked him "almost on a part with Ktesias."8 [Ibid., pp. 18 ff.] Schwanbeck has cited, in his favour, the passage from Arrian's Indika in which both Eratosthenes and Megasthenes are referred to as "approved men." It is, however, curious that Schwanbeck does not refer to the views of Arrian, quoted above, in which he clearly says that no true account of India beyond the Hyphasis is known since the account of Megasthenes is absolutely unreliable; and he supports this by mentioning the latter's description of the river Silas. Again, referring to the statement of Megasthenes 'that the Indian tribes number in all 118,' Arrian makes the very apposite comment: "I am at a loss to conjecture how he arrived at it, for the greater part of India he did not visit, nor is mutual intercourse maintained between all the tribes."9 [Ibid., pp. 198-9.] Again Arrian says: "Megasthenes avers that the tradition about (gold-digging) ants is strictly true," and very correctly observed: "Megasthenes writes what he had heard from hearsay."10 [Ibid., p. 217.] Megasthenes may certainly be excused, as Schwanbeck has argued, for recording "truthfully both what he actually saw, and what was told him by others."11 [Ibid., p. 26.] But when Megasthenes does not evidently distinguish between the two, and avers as strictly true what he merely heard from others, we may certainly be skeptical about the real value of his accounts. Besides, it is obvious from the way in which he has recorded the most unnatural phenomena and incredible tales about men and animals, without any comment, that he did not possess a very high degree of critical judgment such as we find, for example, in the writings of Arrian and Strabo. It is to be seriously considered how far we can place absolute reliance on the statements of such an uncritical man, even if they were based on his own observations. This particularly applies to his description of social manners which would be in any case difficult for a foreigner to comprehend rightly even if he had a higher degree of critical ability than Megasthenes possessed. His description of the seven castes, which are unknown to Indian literature or tradition, may be cited as an example, where, on a few basic facts, he has reared up a structure which is mostly inaccurate and misleading. On the whole, time has surely come when we must make a re-assessment of the nature and value of the Indika of Megasthenes as a source of our knowledge regarding ancient Indian history and culture.