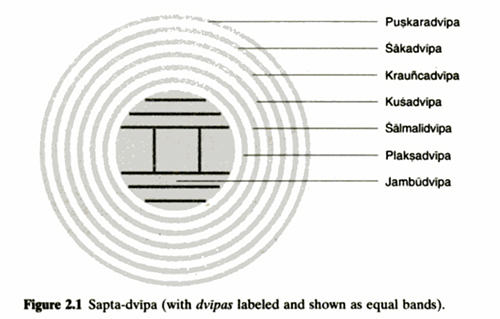
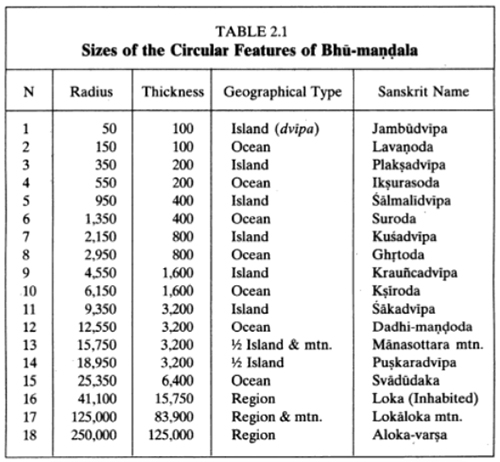
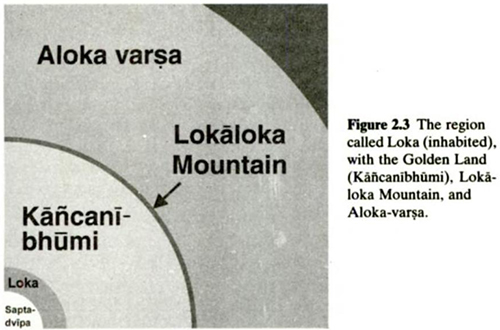
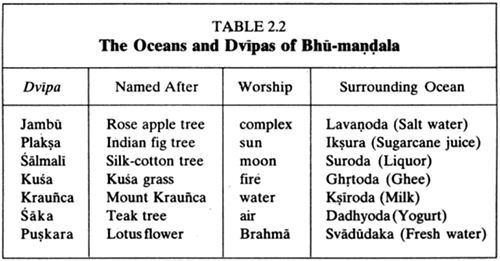
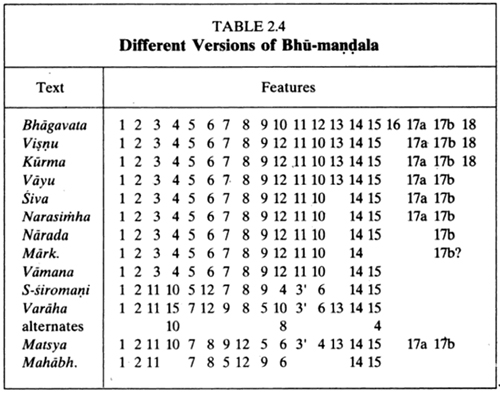
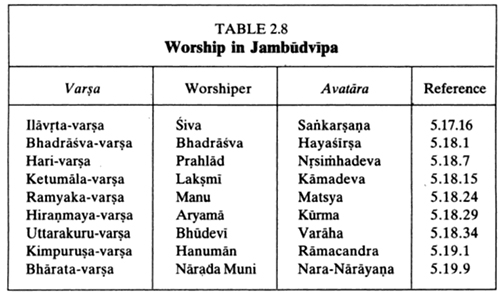
by Wikipedia
Accessed: 5/14/22
Why the focus on religion? Because the role of colonialism (and generally of economic and political interests) in the birth of Orientalism dwindles to insignificance compared to the role of religion....
It is a central thesis of this book that Europe's discovery of Asian religions was deeply linked to the development of Orientalism and its gradual emancipation from biblical studies. The birth of modern Orientalism was not a Caesarean section performed by colonialist doctors at the beginning of the nineteenth century when Europe's imperialist powers began to dominate large swaths of Asia. Rather, it was the result of a long process that around the turn of the eighteenth century produced a paradigm change....
Voltaire's "Indian" campaign ended up playing a crucial role in raising the kind of questions about origins and ancient religions that played at least as important a role in the establishment of state-supported, university-based Orientalism as did the much-touted colonialism and imperialism. Rather than thirst for political and economic power, what was primarily at work here was ideological power: the power of Europe's long-established worldview and religious ideology that Voltaire provocatively labeled "l'infame" and that he tried to destabilize through an avalanche of articles, pamphlets, and books....
The idea of a pan-Asian religion or doctrine -- conceived either positively as an ancient theology or negatively as an ancient idolatry -- was not only common throughout Diderot's century but dominant. It is a subject well worth exploring; after all, almost every chapter of this book shows that this was a far more influential factor in the birth of Orientalism than the much-evoked and blamed colonialism....
This rich religious and ideological background is also bound to remain invisible when looking through the coarse lens of preconceived ideas such as Edward Said's Orientalist "colonialism" or Western "exploitation."...
We have already seen that the emergence in the European mind of a pan-Asiatic religion (that we now readily identify as Buddhism) did not happen overnight in some nineteenth-century study. Such scenarios of a nineteenth-century "creation" of Buddhism grew on a soil fertilized by several biases. The "Indian" bias links the European discovery of Buddhism to India as Buddhism's country of origin, the "textual" bias to the study of Buddhist texts in Indian languages, and the "colonialist" bias posits that such discovery and study were primarily linked to colonial interests. This accounts for the exaggerated role of British "pioneers" in recent studies. Charles Allen's "men who discovered India's lost religion," for example, are without exception British colonialist "Sahibs" (Allen 2002)....
The discovery of long-vanished Indian Buddhism, by contrast, indeed happened to a large extent in the nineteenth-century "European philological workshop" (Masuzawa 2005:126). The present chapter will show, however, that prior to that there were "workshops" not manned by Sanskritists but rather by French missionaries and by academics who studied and translated Arabic and Chinese sources long before the first British colonialists began to dabble in Sanskrit....
"Orientalism" has been portrayed by Edward Said in his eponymous book, first published in 1979, as a very influential, state-sponsored, essentially imperialist and colonialist enterprise. For Said, the Orientalist ideology was rooted in ....
-- The Birth of Orientalism, by Urs App
[A] false dichotomy) is a logical fallacy, which occurs when a limited number of options are incorrectly presented as being mutually exclusive to one another.
-- False Dilemmas and False Dichotomies: What They Are and How to Respond to Them, by Effectiviology
[T]he director of the Paris observatory in the 1670s Gian-Domenico Cassini (1624-1712) submitted a proposal to the minister Colbert to send Jesuits to China to make some astronomical observations, and to advance their knowledge of latitudes, longitudes and magnetic declinations....One of the missions that was sent to Thailand finally landed up in Pondicherry.
A leading French astronomer stationed in China was Pere Antoine Gaubil (1689-1759), whose astronomical researches had exercised influence on the French astronomer, theorist and mathematical physicist, Pierre Simon Laplace (1749-1827)....
Pere Gaubil was in constant touch with the French Jesuit astronomer and cartographer Pere Claude Stanisla Boudier (1687-1757) stationed at Chandernagor in India. Boudier's reputation as an astronomer earned him an invitation to Jai Singh' s court in 1734. During his journey to and sojourn at Jaipur, he, like his counterparts in China determined the longitude of 63 Indian cities, in addition to measuring the meridional altitudes of a few stars. [Ansari 1985: 372]. In addition, he observed the first satellite of Jupiter on April 2, 1734 at Fatehpur, and again at Jaipur on August 15 of the same year. He also observed the solar eclipse of May 3, 1734 at Delhi and had earlier reported the lunar eclipse of December 1, 1732....
Pere Pons arrived in India in 1726 and after spending a few years in Thanjavur was appointed superior of the French Mission in Bengal. Other than compiling a Sanskrit grammar, and a treatise on Sanskrit poetics that was sent to Europe, he visited Delhi and Jaipur with Pere Boudier, mentioned earlier, to make some astronomical observations ...
Perusing these records, we recognise firstly the importance and authority of Gaubil among the Jesuit astronomers in India, for he appeared to be providing them the numbers that they considered standard, and thus aided their calibration. It was Gaubil who forwarded their results to Cassini, and thus the latter was the final authority certifying the results of the expedition. Secondly, the study of the motion of the stars and the planets, enabled the savants, through the Jesuits, to map the co-ordinates of the globe, symbolically weaving Paris, Rome, Delhi, Jaipur and Beijing into the new fabric of modern science of which the Jesuits were the prominent cultural vectors, and subsequently the agents of cultural imperialism.
-- French Jesuit Scientists in India: Historical Astronomy in the Discourse on India, 1670-1770, by Dhruv Raina

Giovanni Domenico Cassini
Born: 8 June 1625, Perinaldo, Republic of Genova
Died: 14 September 1712 (aged 87), Paris, France
Nationality: Italian, French
Alma mater: The Jesuit College at Genoa
Known for: Cassini Division; Cassini identity; Cassini's laws; Cassini oval; First to observe the division in the rings of Saturn
Scientific career
Fields: Mathematics, astrology, astronomy, engineering
Institutions: University of Bologna
Giovanni[a] Domenico Cassini, also known as Jean-Dominique Cassini (8 June 1625 – 14 September 1712) was an Italian (naturalised French)[1] mathematician, astronomer and engineer. Cassini was born in Perinaldo,[2][3] near Imperia, at that time in the County of Nice, part of the Savoyard state.[4][5] Cassini is known for his work on astronomy and engineering. He discovered four satellites of the planet Saturn and noted the division of the rings of Saturn; the Cassini Division was named after him. Giovanni Domenico Cassini was also the first of his family to begin work on the project of creating a topographic map of France.
The Cassini space probe, launched in 1997, was named after him and became the fourth to visit the planet Saturn and the first to orbit the planet.
Life
Time in Italy
Cassini was the son of Jacopo Cassini, a Tuscan, and Giulia Crovesi. In 1648 Cassini accepted a position at the observatory at Panzano, near Bologna, to work with Marquis Cornelio Malvasia, a rich amateur astronomer, initiating the first part of his career.[6] During his time at the Panzano Observatory, Cassini was able to complete his education under the scientists Giovanni Battista Riccioli and Francesco Maria Grimaldi. In 1650 the senate of Bologna appointed him as the principal chair of astronomy at the University of Bologna.[6]
While in his position in Bologna, he observed and wrote a treatise on the comet of 1652. He was also employed by the senate of Bologna as hydraulic engineer, and appointed by Pope Alexander VII inspector of fortifications in 1657. He was subsequently director of waterways in the papal states.[7]
In San Petronio, Bologna, Cassini convinced church officials to create an improved sundial meridian line at the San Petronio Basilica, moving the pinhole gnomon that projected the Sun's image up into the church's vaults 66.8 meters (219 ft) away from the meridian inscribed in the floor. The much larger image of the Sun's disk projected by the camera obscura effect allowed him to measure the change in diameter of the Sun's disk over the year as the Earth moved toward and then away from the Sun. He concluded the changes in size he measured were consistent with Johannes Kepler's 1609 heliocentric theory, where the Earth was moving around the Sun in an elliptical orbit instead of the Ptolemaic system where the Sun orbited the Earth in an eccentric orbit.[8]
Cassini remained in Bologna working until Colbert recruited him to come to Paris to help set up the Paris Observatory. Cassini departed from Bologna on 25 February 1669.[6]
Moving to France

An engraving of the Paris Observatory during Cassini's time. The tower on the right is the "Marly Tower", a dismantled part of the Machine de Marly, moved there by Cassini for mounting long focus and aerial telescopes.
Cassini's determinations of the rotational periods of Jupiter and Mars in 1665–1667 enhanced his fame, and in 1669, with the reluctant assent of the Pope, he moved to France and through a grant from Louis XIV of France helped to set up the Paris Observatory, which opened in 1671;[7] he would remain the director of the observatory for the rest of his career until his death in 1712. For the remaining forty-one years of his life Cassini served as astronomer/astrologer to Louis XIV ("The Sun King"); serving the expected dual role yet focusing the overwhelming majority of his time on astronomy rather than the astrology he had studied so much in his youth. Cassini thoroughly adopted his new country, to the extent that he became interchangeably known as Jean-Dominique Cassini, although that is also the name of his great-grandson, Dominique, comte de Cassini.
During this time, Cassini's method of determining longitude was used to measure the size of France accurately for the first time. The country turned out to be considerably smaller than expected, and the king quipped that Cassini had taken more of his kingdom from him than he had won in all his wars.
On 14 July 1673 Cassini obtained the benefits of French citizenship. In 1674 he married Geneviève de Laistre, the daughter of the lieutenant general of the comté of Clermont. "From this marriage Cassini had two sons; the younger, Jacques Cassini, succeeded him as astronomer and geodesist under the name of Cassini II."[6]
In 1711 Cassini went blind and he died on 14 September 1712 in Paris at the age of 87.[2]
Astronomer
Cassini observed and published surface markings on Mars (earlier seen by Christiaan Huygens but not published), determined the rotation periods of Mars and Jupiter, and discovered four satellites of Saturn: Iapetus and Rhea in 1671 and 1672, and Tethys and Dione (1684).[9] Cassini was the first to observe these four moons, which he called Sidera Lodoicea (the stars of Louis), including Iapetus, whose anomalous variations in brightness he correctly ascribed as being due to the presence of dark material on one hemisphere (now called Cassini Regio in his honour). In addition he discovered the Cassini Division in the rings of Saturn (1675).[6] He shares with Robert Hooke credit for the discovery of the Great Red Spot on Jupiter (ca. 1665). Around 1690, Cassini was the first to observe differential rotation within Jupiter's atmosphere.
In 1672 he sent his colleague Jean Richer to Cayenne, French Guiana, while he himself stayed in Paris. The two made simultaneous observations of Mars and, by computing the parallax, determined its distance from Earth. This allowed for the first time an estimation of the dimensions of the Solar System: since the relative ratios of various sun-planet distances were already known from geometry, only a single absolute interplanetary distance was needed to calculate all of the distances.
In 1677, the English philosopher John Locke visited Cassini in Paris. He writes, "At the Observatory, we saw the Moon in a twenty-two foot glass, and Jupiter, with his satellites, in the same. The most remote was on the east, and the other three on the west. We also saw Saturn and his rings, in a twelve-foot glass, and one of his satellites."[10]
Cassini initially held the Earth to be the centre of the Solar System, though later observations compelled him to accept the model of the Solar System proposed by Nicolaus Copernicus, and eventually that of Tycho Brahe. "In 1659 he presented a model of the planetary system that was in accord with the hypothesis of Nicolaus Copernicus. In 1661 he developed a method, inspired by Kepler's work, of mapping successive phases of solar eclipses; and in 1662 he published new tables of the sun, based on his observations at San Petronio."[6] Cassini also rejected Newton's theory of gravity, after measurements he conducted which wrongly suggested that the Earth was elongated at its poles. More than forty years of controversy about the subject were closed in favour of Newton's theory after the measurements of the French Geodesic Mission (1736 to 1744) and the Lapponian expedition in 1737 led by Pierre Louis Moreau de Maupertuis.
Cassini was also the first to make successful measurements of longitude by the method suggested by Galileo, using eclipses of the Galilean satellites as a clock.
In 1683, Cassini presented the correct explanation of the phenomenon of zodiacal light.[7] Zodiacal light is a faint glow that extends away from the Sun in the ecliptic plane of the sky, caused by dusty objects in interplanetary space.
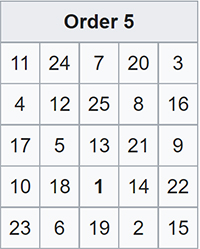
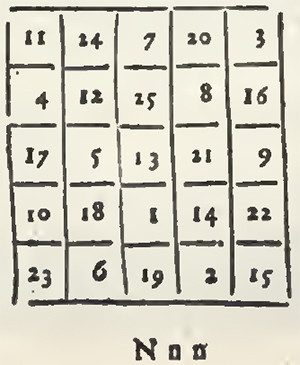
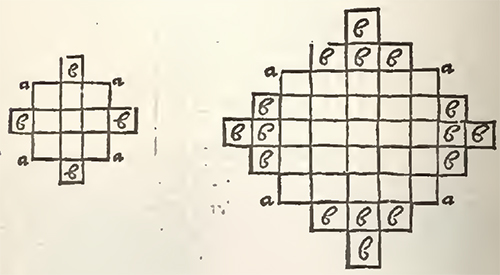
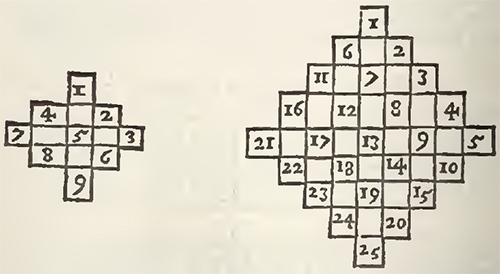
Cassini is also credited with introducing Indian Astronomy to Europe. In 1688, the French envoy to Siam (Thailand), Simon de la Loubère, returned to Paris with an obscure manuscript relating to the astronomical traditions of that country, along with a French translation. The Siamese Manuscript [Rules of the Siamese Astronomy, for calculating the Motions of the Sun and Moon, translated from the Siamese, and since examined and explained by M. Cassini, a Member of the Royal Academy of Sciences, Excerpt from "A New Historical Relation of the Kingdom of Siam, by Monsieur De La Loubere, Envoy Extraordinary from the French King, to the King of Siam, in the years 1687 and 1688. Wherein a full and curious Account is given of the Chinese Way of Arithmetick, and Mathematick Learning. In Two Tomes, Illustrated with Sculptures. Done out of French, by A.P. Gen. R.S.S. 1693", Tome II, Pg. 186], as it is now called, somehow fell into Cassini's hands.
[T]he director of the Paris observatory in the 1670s Gian-Domenico Cassini (1624-1712) submitted a proposal to the minister Colbert to send Jesuits to China to make some astronomical observations, and to advance their knowledge of latitudes, longitudes and magnetic declinations....One of the missions that was sent to Thailand finally landed up in Pondicherry.
-- French Jesuit Scientists in India: Historical Astronomy in the Discourse on India, 1670-1770, by Dhruv Raina
A Greek scholar, who, like Pythagoras, once traveled in India, having learned the sciences of the Bracmanas, taught them in his turn his method of astronomy; and in order that his disciples might make it a mystery to others, he left them in his work the Greek names of the planets, the signs of the zodiac, and several terms like hora (twenty-fourth part of a day), Kendra (center), etc. I had this acquaintance at Dely, and it served me to make the astronomers of Raja Jaesing, who are in large numbers in the famous observatory which he had built in this capital, feel that formerly masters had come to them [from] Europe.
When we arrived at Jaëpur, the prince, to convince himself of the truth of what I had advanced, wanted to know the etymology of these Greek words, which I gave him.... Raja Jaësing will be regarded in the centuries to come as the restorer of Indian astronomy. The tables of M. de la Hire, under the name of this Prince, will be current everywhere in a few years.
-- Letter From Father Pons, Missionary of the Company of Jesus, to Father Du Halde, of the same Company. At Careical, on the coast of Tanjaour; in the East Indies, November 23, 1740. From "Lettres Edifiantes Et Curieuses, Ecrites Des Missions Etrangeres", by Charles Le Gobien
He was intrigued enough by it to spend considerable time and effort deciphering its cryptic contents, also determining on the way that the document originated in India.[11]
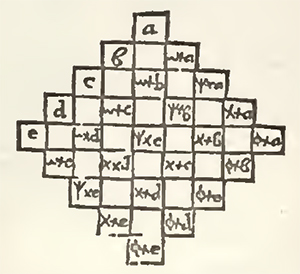
Curiously enough the first definite information respecting the Hindu system of astronomy, came to Europe from Siam, where, in the early centuries of our era, there was a flourishing Hindu state. In 1687 Louis XIV sent M. de la Loubere on an embassy to Siam, and he brought back with him a portion of a manuscript containing rules for computing the places of the sun and moon. This was submitted to the celebrated John Dominic Cassini, the Italian astronomer, whom Louis had brought to Paris to take charge of his observatory. In his hands the calculations described, without indication of the meaning of the constants employed, were lucidly explained. [!!!] His memoir was published in 1691, in De la Loubere's Relation de Siam (tome ii.), and afterwards reprinted with other papers by Cassini in the eighth volume of the Memoires de l'Academie Royale des Sciences, for 1666 to 1699 (pp. 279-362).
Cassini's principal deductions from the Siamese manuscript were -- (1) That the sidereal year employed was of 365d. 6h. 12m. 36s., being the 800th part of 292,207 days; (2) That the epoch of the constants was Saturday, 21st March, 638 A.D. at new moon (the mean conjunction occurring at Siam about 3h. 15m. A.M.) and when there was a considerable eclipse of the sun at 5h. 19m. P.M., 1 [I have revised the times from modern tables, assuming the longitude of Siam at 6h. 42m. E. from Greenwich; Cassini (Mem, de l'Acad, tome viii. p. 311) adopted 6h. 34m. E. from Paris, which is only 1-1/2m. in excess of this.] which eclipse, however, could not have been visible to the east of Orissa; (3) That since a correction to that effect is applied to the results, the rules and data were originally arranged for a place about 18-1/4°to the west of Siam: this he conjectures to have been "Narsinga,"2 [Mem. de l'Acad. 1666-1699, tome viii. p. 309.] which Bailly places "in Orissa" in lat. 17° 22' N., that is, about Pittapuram in the Godavari district; but Bailly suggests Benares as a more probable place, and "having about the same longitude";3 [Astron. Indienne et Orientale, p. 12.] (4) That at the epoch the sun's apogee was at 20° of Cancer, and the moon's at 21° of Capricorn; (5) That to the revolution of the moon's apsis a period of 3232 days was allowed; (6) That the greatest equation of the centre for the sun was 2° 12', though he gives a short table from the manuscript on the same page, which states it at 2° 14', while Bailly, professing to quote Cassini's figures, says4 [Astron. Indienne, p. viii. 7, 44.] he found it to be 2° 10' 32" -- which is the value assigned in the Surya Siddhanta, and which Bailly himself had obtained from another Indian work.5 [Mem. de l'Acad. tome viii. p. 304.] The moon's greatest equation of the centre Cassini found to be 4° 56'; (7) That the civil year began with the month of Karttika; (8) And that the constants employed made the artificial day or tithi bear to the civil or natural day the ratio of 692:703; hence 703 lunar months are equal to 20,760 days, and the synodical month was 29d. 12h. 44m. 2-39s.; and as 228 solar months were made equal to 235 lunar ones, he concluded that in 13,357 years there are 165,205 lunar months and 487,860 days, whence he deduced a tropical year of 365d. 5h. 55m. 13-77s., or almost exactly the same as Ptolemy's value.
7. With respect to these results, it may be noted -- (1) That the sidereal year of 365d. 6h. 12m. 36s. is exactly that of the now missing Paulisa-Siddhanta, and, from Al-Beruni's account of it, we learn that it used the same numbers as the Siamese to determine the year, viz. 292,207 days as the measure of 800 years.1 [Al-Beruni's India, Sachau's transl. vol. ii. p. 58; see below § 38.] (2) The ratio of the tithi to the natural day is a usual approximation in Hindu astronomy, giving 1 kshaya tithi in 64-1/11 or 63-10/11 days.2 [Wilkinson's Siddhanta S'iromani, Goladhyaya, iv. 12, where it is misprinted 64-1/11 for 64-1/11; conf. also Al-Beruni's India, Sachau's tr. vol. ii. pp. 37, 47, 52, and 54.] (3) But the ratio of 228 solar months (6939-6871 days), is introduced in the computations only where so close an approximation could produce no sensible error in the results; and Cassini has, perhaps, been misled here by the natural supposition that a tropical year must be as material an element in Hindu as it is in European astronomy. (4) From Al-Beruni, again, we learn that Pulisa assigned 488,219 revolutions of the moon's apsis to a Chaturyuga,3 [Al-Beruni's India, vol. ii. p. 18: the exact value with this element is 3231-98752 days, the difference between this and 3232 days amounts only to one day in 80-2 revolutions, or 686 years.] or almost exactly 3232 days to a revolution. We might infer, then, that the other elements used were also taken from the Paulisa-Siddhanta -- that the lunar month, for example, was of 29d. 12h. 44m. 2-75s. -- but that they had been engrossed in a Karana for the calculation of horoscopes and almanacs. This points, however, to Siam and the Eastern Peninsula as a promising field of search for the Paulisa1 [This portion of the paper was written before Thibaut's Panchasiddhantika, of Varaha Mihira, reached this country. It contains an outline of the Paulisa Siddhanta.] and possibly others of the Siddhantas that have been lost in India.
8. The next contribution to our knowledge of this subject is to be found in an appendix to the Historia Regni Graecorum Bactriani of T.S. Bayer (1694-1738), and is titled "Christophori Theodosii Waltheri Doctrina Temporum Indica ex libris Indicis et Brahmanum institutione, A.C. clclccxxxiii Trangambarae digesta, simul cum Paralipomenis recentioribus."2 [Petropoli, 1738.] The author remarks that Ptolemy alone divided the day into sixty parts, as the Hindus do, and these again sexagesimally. He cites the Hindu divisions of time from Amarasimha; gives the names of the nine graha in Sanskrit and Tamil; of the days of the week; of the months; the signs of the zodiac; the nakshatras, yogas, karanas; of the tithis in Sanskrit, Persian, and Dekhani; and an account of the yugas, and of the Panchanga or kalendar. To this curious tract is added a long note by Leonard Euler on the Hindu year of 365d. 6h. 12m. 30s.
9. Beschi had also given some account of the Indian almanac in his Tamil Grammar, published in 1738;3 [Beschi († 1742) also published Tiruchabei Kanidam, a Tamil work on astronomy.] but no contribution of real importance to Hindu astronomy was made for about eighty years after Cassini's paper.
-- Burgess, James (1893). "Notes on Hindu Astronomy and the History of Our Knowledge of It". Journal of the Royal Asiatic Society of Great Britain & Ireland: 722–723.
The Pauliṣa Siddhānta (literally, "The scientific-treatise of Pauliṣa Muni") refers to multiple Indian astronomical treatises, at least one of which is based on a Western source. "Siddhānta" literally means "doctrine" or "tradition".
It is often mistakenly thought to be a single work and attributed to Paul of Alexandria (c. 378 CE). However, this notion has been rejected by other scholars in the field, notably by David Pingree who stated that "...the identification of Paulus Alexandrinus with the author of the Pauliṣa Siddhānta is totally false". Similarly, K. V. Sarma writes that it is from a Greek source, known only as Pauliṣa.
The Alberuni wrote that the Siddhanta is based to the teaching of a Greek named Paulus.
The earlier Pauliṣa-siddhānta dates from the third or fourth century, and the later Pauliṣa-siddhānta from the eighth century.
Similar to the Yavanajātaka ("The Sayings of the Greeks"), the Pauliṣa Siddhānta is an example of Hellenistic astronomy (especially the Alexandrian school) in India during the first centuries CE.
The Pauliṣa Siddhānta was particularly influential on the work of the Indian astronomer Varāhamihira. It was considered one of "The Five Astronomical Canons" in India in the 5th century.
-- Paulisa Siddhanta, by Wikipedia
His explication of the manuscript appeared in La Loubère's book on the Kingdom of Siam in 1691,[12].
Ziegenbalg attributes the decline of the Catholic missions in part to the rivalry between their orders, and mentions the visit of the Papal legate Charles de Tournon to Pondicherry in 1703-1704, and his desire to rid the church of 'heathen' elements introduced by the missionaries, such as "the smearing of ash on the forehead, the shameful difference in the church and in the distribution of holy communion between high and low castes, the play-acting in Brahman habits, etc." He reports also what he has heard of Jesuit missions in China and Thailand, claiming that everywhere Jesuit cunning and unscrupulousness has eventually led to their ruin. [Many of the Jesuits in the Carnatic mission had been forced to leave Thailand in 1688.]
-- Bartholomäus Ziegenbalg, the Tranquebar Mission, and `the Roman Horror'
in Andreas Gross, Y. Vincent Kumaradoss, and Heike Liebau, eds., Halle and the Beginning of Protestant Christianity in India, vol. 2 (Halle: Verlag der Franckeschen Stiftungen zu Halle, 2006), 797–811, by Will Sweetman
Elizabeth (Lisa) Lyons is another great collector of Thai manuscripts who was living in Bangkok around the same time as Sarah Bekker. ...
One of the many items Lyons acquired for the Penn collection was as beautiful as Bekker’s Abhidhamma chet gamphi (Penn Libraries Ms. Coll. 990, Item 5). However, the authors found it, with some help from Forrest McGill at the Asian Art Museum (San Francisco), a bit “too beautiful.” They examined this manuscript held in the Penn Museum of Archaeology and Anthropology (Ms. 89-13-251). Initially this manuscript was loosely dated to the 1870s, but unlike manuscripts in other collections (including Penn’s), there was very little damage. The condition of the manuscript, including the cover, was remarkable. The authors were very pleased, and when they opened the manuscript they were further impressed with the quality of the paper and the dark color of the text (thin mul style khom script). There was no water damage and no marginalia or corrections (again—remarkable). The quality of the paintings is what was really striking. The colors were vibrant, the details fine, and the scenes iconic. The gold used in the paintings (a common feature of Thai manuscripts is to have actual gold leaf in paint) had not faded and was much thicker than any other example from the eighteenth or nineteenth centuries. It was a perfect manuscript for a museum display, the authors thought, as it would be appreciated for its beauty and show the value of good conservation efforts. However, they were a little suspicious of the dating to 1870s by Lyons and furthermore had not encountered a manuscript of this quality. McDaniel asked Forrest McGill for his opinion, and he immediately assumed it was made post-1950s and suggested, a suggestion the authors now think is correct, that it could be a forgery. McGill had seen forgeries like this done by a local artist from Thailand who had attempted to pass on fake manuscripts to foreign institutions in the 1970s. That suggestion led Kerekes and McDaniel to look closely at the paintings and compare them to others they had seen in other manuscripts. Indeed, one painting is directly copied, it seems, from a Phra Malai manuscript now held at the Chester Beatty Library (and mentioned in another article in this issue). In one painting, four monks with grotesque faces are seen reading a large manuscript, drinking tea, and chewing betel nut (a nice piece of social historical evidence for sure) while a half-naked woman and her children ignore the monks and play a board game in front of them (F.A6.L). The right side of the same folio depicts two men drinking tea and smiling coyly at each other on the grounds of a monastery, while a third man is seen in the window of the monastery in a way that suggests he is either napping or being pleasured orally by an unseen person. These scenes appear in other extant Thai manuscripts, but here the paintings in the Penn manuscript and the Chester Beatty Library (whose date we can confirm as from the nineteenth century) are nearly identical and the scenes are unique enough that there is no other explanation besides direct copying. It is known that the forger in question knew several manuscripts in Western collections. In another scene, the artist seems to have been trying to have a little salacious, or perhaps perverted, fun. In a common scene from Phra Malai manuscripts, we find men fighting with knives. This scene represents the fate of human beings near the end of the world. However, in this particular painting, the artist inserts a woman into the middle of the fight and graphically depicts her having intercourse with one of the fighting men. One could interpret this as a rape scene, but the woman is smiling and the other men seem to ignore her (F.B26.R). This is certainly unusual, even though Thai artists in the nineteenth century sometimes inserted scenes suggesting sexual encounters. There is little evidence from older manuscripts that graphically depict intercourse or fully naked women and men.
Kerekes noted two particular features of this “too beautiful” manuscript that also led the authors to suspect a late forgery. First, there are clearly newer painted folios that have been inserted into an older text as scenes from cleverly hidden and glued page breaks (F.B42.TB.LR). This could be a sign that an older text was added to make this new text larger or that paintings were removed and sold from an older manuscript and new paintings inserted. Second, on one page is a short sentence in modern Thai script in a manuscript that is otherwise in the Thai language in khom script (F.A12.B.M). The line tells the reader to take a break and drink tea! This is not found in other manuscripts and seems to have been a clever little joke. In conclusion, sometimes certain manuscripts are too good to be true, and forgeries do exist. Collectors often pay significant amounts of money for manuscripts, and when markets are created, sometimes, as in all situations, people rise to supply goods for that new market. When that market is premodern art, artists are sometimes tempted to create a “supply.”
Conclusion
Collections and collectors of Siamese/Thai manuscripts in the United States are vast in number and largely unexplored. This short overview was designed to be a roadmap for future scholars who seek to investigate individual manuscripts held at the University of Pennsylvania, The Walters Art Museum, and other collections, or begin to fully investigate the unstudied collections of Cornell, the University of Michigan, or the Library of Congress.
-- Siamese Manuscript Collections in the United States, by Susanne Ryuyin Kerekes, University of Pennsylvania and Justin McDaniel, University of Pennsylvania
Astrologer
Attracted to the heavens in his youth, his first interest was in astrology. While young he read widely on the subject of astrology, and soon was very knowledgeable about it; this extensive knowledge of astrology led to his first appointment as an astronomer. Later in life he focused almost exclusively on astronomy and all but denounced astrology as he became increasingly involved in the Scientific Revolution.
In 1645 the Marquis Cornelio Malvasia, a senator of Bologna with a great interest in astrology, invited Cassini to Bologna and offered him a position in the Panzano Observatory, which he was constructing at that time. Most of their time was spent calculating newer, better, and more accurate ephemerides for astrological purposes using the rapidly advancing astronomical methods and tools of the day.
Engineering
In 1653, Cassini, wishing to employ the use of a meridian line, sketched a plan for a new and larger meridian line but one that would be difficult to build. His calculations were precise; the construction succeeded perfectly; and its success gave Cassini a brilliant reputation for working with engineering and structural works.[6]
Cassini was employed by Pope Clement IX in regard to fortifications, river management, and flooding of the Po River. "Cassini composed several memoirs on the flooding of the Po River and on the means of avoiding it; moreover, he also carried out experiments in applied hydraulics."[6] In 1663 he was named superintendent of fortifications and in 1665 inspector for Perugia.[6] The Pope asked Cassini to take Holy Orders to work with him permanently but Cassini turned him down because he wanted to work on astronomy full-time.
In the 1670s, Cassini began work on a project to create a topographic map of France, using Gemma Frisius's technique of triangulation. The project was continued by his son Jacques Cassini and eventually finished by his grandson César-François Cassini de Thury and published as the Carte de Cassini in 1789[13] or 1793.[14] It was the first topographic map of an entire country.
Works
• Specimen observationum Bononiensium (in Latin). Bologna: eredi Evangelista Dozza (1.). 1656.
• Martis circa axem proprium revolubilis observationes Bononiae habitae (in Latin). Bologna: eredi Evangelista Dozza (1.). 1666.
• Spina celeste meteora osservata in Bologna il mese di marzo 1668 (in Italian). Bologna: Emilio Maria Manolessi & fratelli. 1668.
• Observations astronomiques faites en divers endroits du royaume, pendant l'année 1672 (in French).
• Abregé des observations et des reflections sur la comete qui a paru au mois de Decembre 1680, et aux mois de Ianvier, Fevrier et Mars de cette annee 1681 (in French). Paris: Estienne Michallet. 1681.
• Cassini, Giovanni Domenico (1682). Raccolta di varie scritture, e notitie concernenti l'interesse della remotione del Reno dalle Valli fatta in Bologna l'anno 1682. (In Bologna): [s.n.]
• Elemens de l'astronomie (in French). Paris: Imprimerie Royale. 1684.
• Découverte de la lumiere celeste qui paroist dans le zodiaque (in French). Paris: Imprimerie Royale. 1685.
• Régles de l'astronomie indienne pour calculer les mouvemens du soleil et de la lune (in French). Paris: Sébastien Mabre-Cramoisy, veuve. 1689.
• De l'origine et du progres de l'astronomie et de son usage dans la geographie et dans la navigation (in French). Vol. 1. Paris: Imprimerie Royale. 1693.
• Hypotheses et les tables des satellites de Jupiter, reformeés sur de nouvelles observations (in French). Paris: Jean Anisson. 1693.
• Meridiana del tempio di S. Petronio tirata e preparata per le osservazioni astronomiche l'anno 1655 (in Italian). Bologna: eredi Vittorio Benacci. 1695.
• Description et usage du planisphere céleste (in French).
• Cassini's works digitalized and available on the digital library of Paris Observatory
See also
• 24101 Cassini, an asteroid
• Aerial telescope – large telescopes used by Cassini
• Cassini (lunar crater)
• Cassini (Martian crater)
• Cassini Division in Saturn's rings
• Cassini oval
• Cassini Regio, dark area on Iapetus
• Cassini–Huygens Mission to Saturn
• Cassini's identity for Fibonacci numbers
• Cassini's laws
• History of the metre
• Neith (hypothetical moon)
• Seconds pendulum
References
1. His name may also be spelled Giovan Domenico Cassini or Gian Domenico Cassini.
1. Joseph A. Angelo, Encyclopedia of Space and Astronomy, Infobase Publishing – 2014, page 114
2. "Giovanni Domenico Cassini (June 8, 1625 – September 14, 1712)". Messier Seds.org. Retrieved 31 October 2012.
3. "Giovanni Domenico Cassini: The rings and moons of Saturn". Surveyor in Berlin.de. Archived from the original on 24 June 2013. Retrieved 31 October 2012.
4. Augusto De Ferrari (1978), "Cassini, Giovan Domenico" Dizionario Biografico degli Italiani 21 (Rome: Istituto dell'Enciclopedia Italiana).
5. Gandolfo, Andrea. La provincia di Imperia: storia, arti, tradizioni. Blue Edizioni, 2005.
6. Cassini, Gian Domenico (Jean-Dominique) (Cassini I). Complete Dictionary of Scientific Biography. Detroit: Charles Scribner's Sons, 2008. pp. 100–104. retrieved 30 May 2013.
7. One or more of the preceding sentences incorporates text from a publication now in the public domain: Clerke, Agnes Mary (1911). "Cassini s.v. Giovanni Domenico Cassini". In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 5 (11th ed.). Cambridge University Press. p. 459.
8. Broad, William J. (19 October 1999). "How the Church Aided 'Heretical' Astronomy". New York Times.
9. Van Helden, Albert (2009). "The beginnings, from Lipperhey to Huygens and Cassini". Experimental Astronomy. 25 (1–3): 3. Bibcode:2009ExA....25....3V. doi:10.1007/s10686-009-9160-y.
10. Locke, John (1864). The life and letters of John Locke : with extracts from his journals and common-place books. London: Bell & Daldy. p. 73.
11. Burgess, James (1893). "Notes on Hindu Astronomy and the History of Our Knowledge of It". Journal of the Royal Asiatic Society of Great Britain & Ireland: 722–723.
12. de La Loubère, Simon (1693). A New Historical Relation of the Kingdom of Siam. Translated by A.P. pp. 64–65. Retrieved 16 October 2017.
13. "Cesar-Francois Cassini de Thury (French surveyor)". Encyclopædia Britannica. Retrieved 5 November 2013.
14. "How topographic map is made – making, history, used, History, Map Scales, Symbols, and Colors, The Manufacturing Process of topographic map, Quality Control, The Future". Madehow.com. 2 September 2013. Retrieved 5 November 2013.
Further reading
• Dominique, comte de Cassini, Giovanni Dominico Cassini biography
• Barkin, Iu. V. (1978). "On Cassini's laws". Astronomicheskii Zhurnal. 55: 113–122. Bibcode:1978SvA....22...64B.
• Connor, Elizabeth (1947). "The Cassini Family and the Paris Observatory". Astronomical Society of the Pacific Leaflets. 5 (218): 146–153. Bibcode:1947ASPL....5..146C.
• Cassini, Anna, Gio. Domenico Cassini. Uno scienziato del Seicento, Comune di Perinaldo, 1994. (Italian)
• Giordano Berti (a cura di), G.D. Cassini e le origini dell'astronomia moderna, catalogo della mostra svoltasi a Perinaldo -Im-, Palazzo Comunale, 31 agosto – 2 novembre 1997. (Italian)
• Giordano Berti e Giovanni Paltrinieri (a cura di), Gian Domenico Cassini. La Meridiana del Tempio di S. Petronio in Bologna, Arnaldo Forni Editore, S. Giovanni in Persiceto, 2000. (Italian)
• De Ferrari, Augusto (1978). "Cassini, Giovan Domenico". Dizionario Biografico degli Italiani (in Italian). Enciclopedia Italiana. Retrieved 2 December 2016.
• Narayanan, Anil, History of Indian Astronomy: The Siamese Manuscript, Lulu Publishing, 2019.
External links
• This article incorporates text from a publication now in the public domain: Herbermann, Charles, ed. (1913). "Giovanni Domenico Cassini". Catholic Encyclopedia. New York: Robert Appleton Company.
• O'Connor, John J.; Robertson, Edmund F., "Giovanni Domenico Cassini", MacTutor History of Mathematics archive, University of St Andrews
• Giovanni Domenico Cassini – complete digitization of 14 volumes belonging to the Old Fund's Department of Astronomy, University of Bologna, held to mark the celebrations of the Cassini in 2005 (website in Italian)
• Giovanni Cassini Biography -Space.com
• esa.int — Jean-Dominique Cassini: Astrology to astronomy -ESA
• Geoastro.de Earth shape
• Virtual exhibition on Paris Observatory digital library